19

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Поверхности второго порядка

Учебно-методическое пособие по специальности «Химия» 020101 (011000).

ВОРОНЕЖ

2006

Утверждено научно-методическим советом математического факультета

15 Марта 2006 года

Протокол №7

Составители: Баев А.Д., Петрова Е.В., Провоторов В.В.

Учебно-методическое пособие подготовлено на кафедре уравнений

в частных производных и теории вероятностей

математического факультета Воронежского госуниверситета

Рекомендуется для студентов 1 курса дневного отделения

химического факультета

1. Функции нескольких переменных

1.1. Общие понятия

Для функции одной переменной: по некоторому правилу ставится в соответствие единственное значение . – область определения функции; - область ее изменения. Часто оказывается, что некоторая переменная величина зависит не от одной, а от двух и большего числа независимых переменных.

Пример 1. Площадь прямоугольника со сторонами и . . Каждой паре значений соответствует определенное значение .

Пример 2. Работа тока на участке цепи: - три переменных и т.д.

Между функциями одной переменой и функциями нескольких переменных имеются существенные различия. В то же время переход от двух переменных к большему числу переменных обычно не встречает затруднений. Поэтому подробно рассмотрим функции двух переменных.

1.2. Понятие функции двух переменных. Область определения. График. Линии уровня

Определение. Если каждой паре значений независимых переменных , взятых из некоторой области изменения, по некоторому закону ставится в соответствие определенное значение третьей переменной , то называется функцией двух переменных и :

.

Например: .

Переменные и называются аргументами функции . Область - область определения функции .

Каждой паре чисел на плоскости можно поставить в соответствие точку . Тогда функцию двух переменных можно понимать как функцию точки на плоскости .

Каждой точке из некоторого множества точек плоскости ставится в соответствие определенное значение переменной : . Плоскость - плоскость аргументов для функции двух переменных. Область определения функции двух переменных – некоторая область плоскости .

Определение. - окрестностью точки называется внутренняя часть круга радиуса с центром в точке

или

.

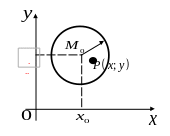
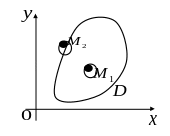
Точка называется внутренней точкой множества , если у этой точки есть окрестность, состоящая из точек данного множества.

Точка называется граничной точкой множества , если любая окрестность этой точки содержит как точки принадлежащие множеству , так и точки ему не принадлежащие.

Сама граничная точка может принадлежать множеству D, а может и не принадлежать.

Определение. Совокупность всех граничных точек множества называется его границей.

Определение. Множество называется замкнутым ( ), если оно содержит все свои граничные точки. Множество называется открытым, если все его точки являются внутренними.

Пример 1. (замкнутый круг).

Пример 2. (открытый круг).

Здесь точки окружности (границы) множеству не принадлежат.

О пределение. Множество точек плоскости называется областью, если:

1. – открытое множество, т.е. состоит только из внутренних точек.

2.Всякие две точки и можно соединить непрерывной линией, все точки которой также принадлежат (свойство связанности).

Открытая область является аналогом интервала на прямой.

Замкнутая область - аналог отрезка .

Найдем области определения функций.

Пример 3. ; ; .

Замкнутый круг – аналог отрезка (рис. 1).

Пример 4. ; ; .

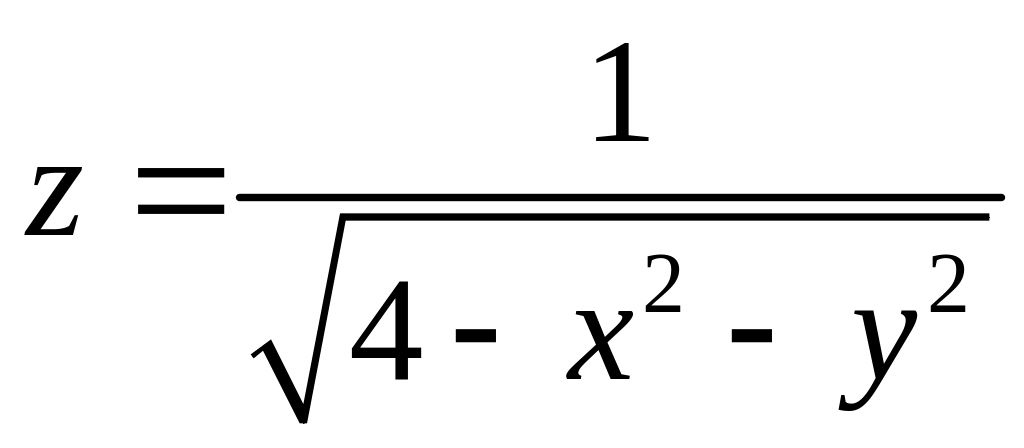Открытый круг – аналог интервала (рис. 2).

П ример 5. ;

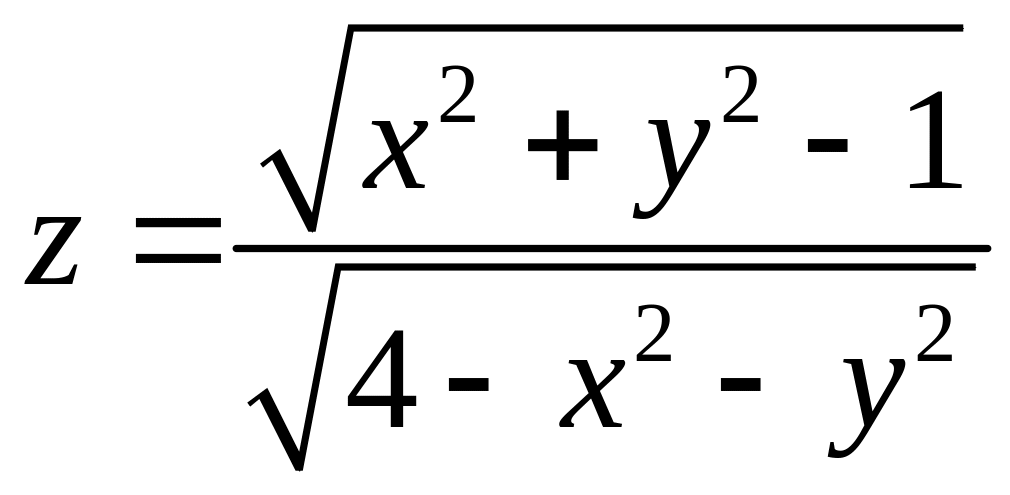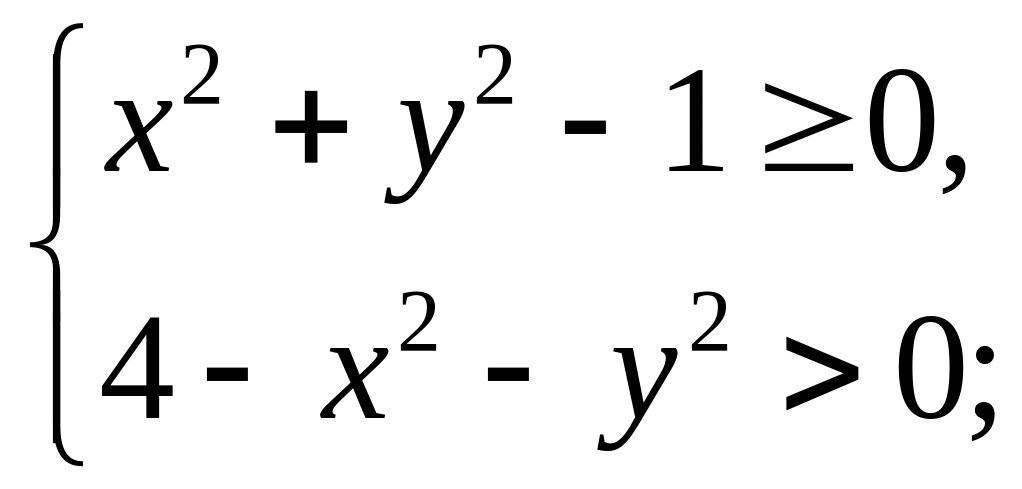
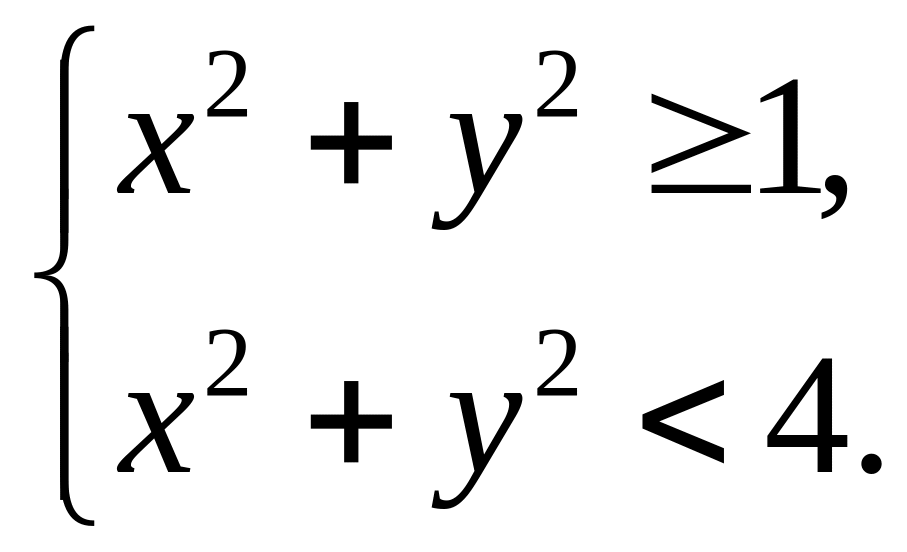
Кольцо – аналог полуинтервала (рис. 3).

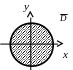
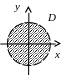
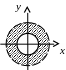
рис. 1 рис. 2 рис. 3

Д ля функции графиком является кривая на плоскости . Функция двух переменных также допускает непосредственное геометрическое истолкование.

Возьмем пространственную декартову систему координат. Функция определена в области плоскости аргументов . Выберем в области произвольную точку и вычислим соответствующее значение функции .

Т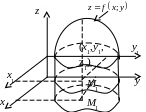 ройку чисел изобразим точкой в координатном пространстве . Если точку перемещать в области определения функции точка опишет некоторую поверхность с уравнением .

Эта поверхность и служит геометрическим образом функции двух переменных, ее графиком.

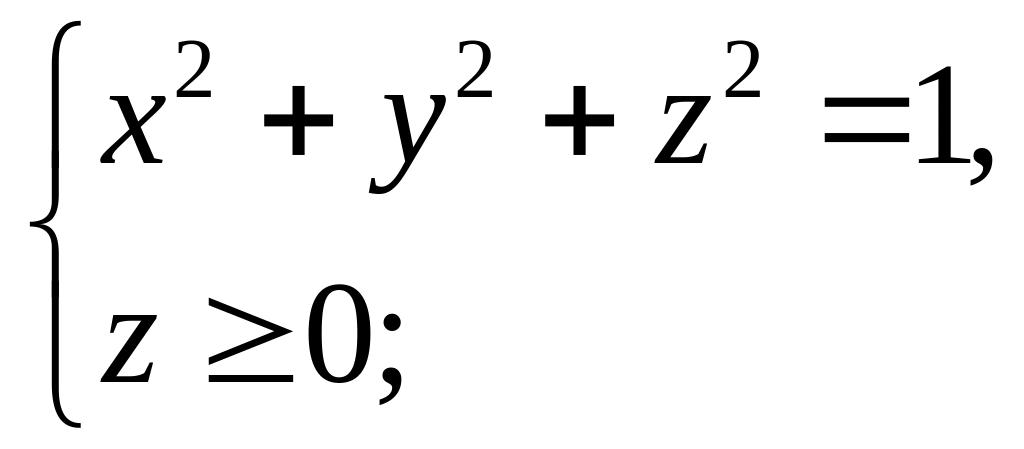
Пример 6. ; ; (верхняя полусфера).

Пример 7. ; - вся плоскость .

График функции проектируется в область определения функции .

Часто вместо графика функции практически более удобным является другой способ представления функции двух переменных – линии уровня.

Определение. Множество точек на плоскости , в которых функция сохраняет постоянное значение : называется линией уровня функции.

Пример 8. Для функции линиями уровня являются окружности с центром в начале координат:

.

В каждой точке линии уровня значения функции постоянны и равны . Выбираем разные , получим разные линии уровня.

Геометрически линии уровня получаются, если пересекать поверхность плоскостями, параллельными плоскости : и проектировать линии пересечения на плоскость . В результате в области определения получается своеобразная «геодезическая карта» поверхности , которая дает представление об изменении функции .

В той части области , где линии уровня сгущаются, функция быстро возрастает или убывает. Там, где линии уровня разрежены, изменяется медленно. В точках экстремума функции линии уровня вырождаются в точку.