
- •Содержание
- •Введение
- •1. Общие сведения о системах автоматического управления и регулирования
- •1.1. Основные принципы управления
- •Рис 1.1. Объект управления
- •1.2. Разновидности и свойства сар
- •1.3. Законы регулирования.
- •1.4. Виды задающих и возмущающих воздействий.
- •2. Математическое описание сар и передаточные функции.
- •2.1 Математическое описание элементов и систем автоматического регулирования.
- •2.2. Передаточные функции.
- •2.3. Структурные схемы и структурные преобразования.
- •Правила структурных преобразований
- •2.4. Структурные модели сар.
- •Рис 2.4. Структурная модель сар
- •3. Характеристики сар и типовых звеньев
- •3.1 Временные характеристики сар.
- •Изображение по Лапласу и оригиналы.
- •3.2. Частотные характеристики сар
- •3.3. Разновидность типовых звеньев сар.
- •Временные характеристики типовых звеньев
- •Частотные характеристики звеньев.
- •4. Устойчивость и качество сар.
- •4.1. Основные условия устойчивости.
- •4.2. Алгебраический критерий устойчивости Гурвица.
- •4.3. Частотный критерий устойчивости Михайлова.
- •4.4. Частотный критерий устойчивости Найквиста.
- •4.5. Оценки качества регулирования.
- •4.6. Коррекция сар.
- •Список литературы.
Правила структурных преобразований
|
Преобразование |
Структурная схема | |
|
Исходная |
Эквивалентная | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Более полный перечень правил структурных преобразований представлен в учебном пособии [1].
Найденные с помощью правил структурных преобразований передаточные функции позволяют достаточно просто определить временные и частотные характеристики и получить качественные и количественные оценки динамики и статики САР.
2.4. Структурные модели сар.
В данном вопросе рассматривается аналитическая форма представления динамических САР и материализация математических понятий и аналитических приемов в виде структурных математических модулей. Это положение в значительной степени упрощает процесс технической реализации как модулей, так и реальных элементов и систем.
Допустим, что САР содержит один вход X ( t ), один выход Y ( t ), и имеет передаточную функцию следующего вида:
![]()
![]() Запишем
уравнение в операторном виде, связывающее
входные и выходные сигналы и соответствующее
заданной передаточной функции:
Запишем
уравнение в операторном виде, связывающее
входные и выходные сигналы и соответствующее
заданной передаточной функции:
(2.12)
Выразим уравнение (2.12) относительно старшей степени S:
![]()
(2.13)
Входной сигнал Y ( t ) можно получить путем последовательного интегрирования старшей производной Sny( t ). Для этого потребуется n последовательно включенных интеграторов, сигналы на входах которых представляют собой производные от Sny ( t ) до Sy( t ) (рис.2.3).
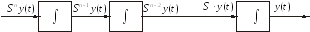
Рис. 2.3. Последовательное интегрирование
Согласно уравнению (2.13) очевидно, что старшая производная Sny( t ) равна переменной bmx ( t ) минус сумма выходных сигналов интеграторов, умноженных на коэффициенты а1, а2 ... аn. Тогда получим структурную модель, представленную на рис. 2.4.
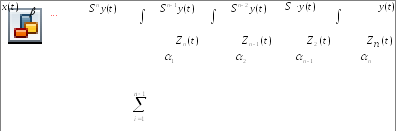
![]()
![]()
![]()
![]()
![]()
Рис 2.4. Структурная модель сар
Введем обозначения Z1(t)=y(t), Z2(t)=Sy(t)…Zn(t)=Sn-1y(t) и уравнение n-го порядка (2.12) запишем в виде системы n дифференциальных уравнений первого порядка:
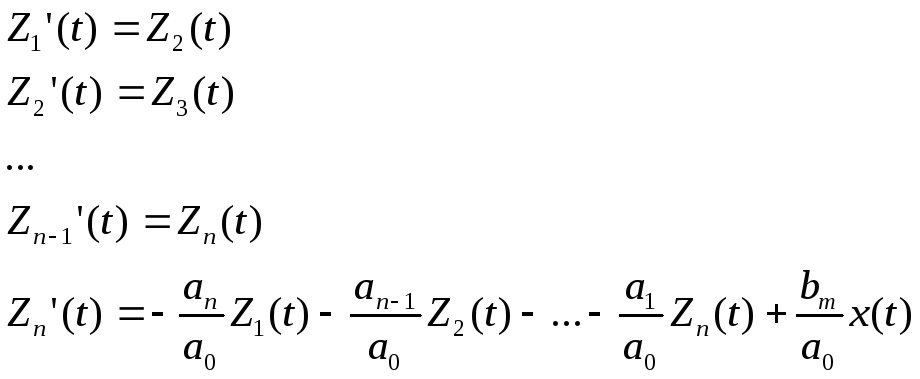
(2.14)
Система уравнений (2.14) является одной из форм представления динамических процессов структурной модели, изображенной на рис. 2.4.
В матричной форме система уравнений (2.14) имеет вид:
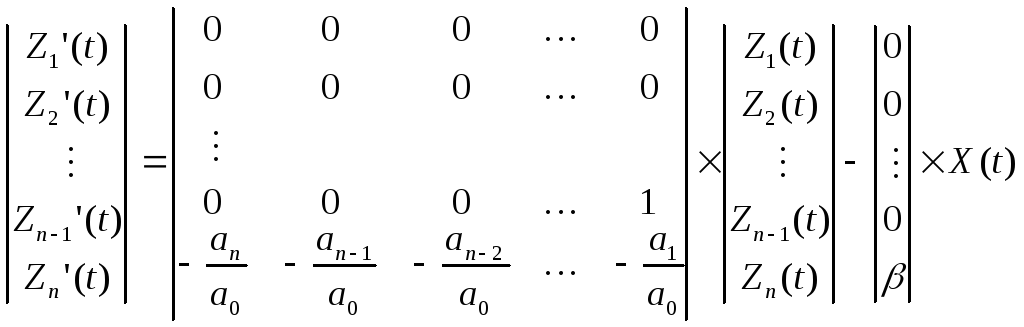
В![]() сокращенном виде матричная форма
записывается следующим образом:
сокращенном виде матричная форма
записывается следующим образом:
где
![]() n-мерный
вектор состояния;
n-мерный
вектор состояния;
A – квадратная матрица размером n n;
-
![]() - вектор-столбец управления.
- вектор-столбец управления.
Структурная математическая модель динамических процессов САР обладает рядом преимуществ перед аналитическими описаниями или передаточными функциями. Во-первых, структурная модель дает ясное и наглядное представление понятию "состояние систем", как совокупность сигналов на выходах интеграторов. Во-вторых, однозначно представляется структура взаимодействий между переменными в виде системы с обратными связями, которые и определяют протекание динамических процессов. Одновременно структурные модели оказывают помощь при моделировании САР на аналоговых или цифровых вычислительных машинах.

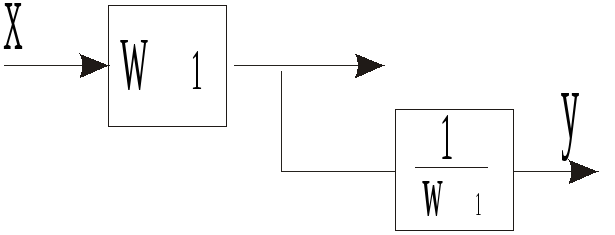
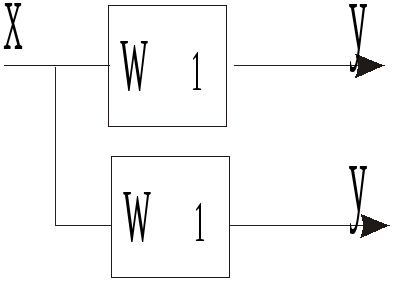 Перенос
точки разветвления через элемент
Перенос
точки разветвления через элемент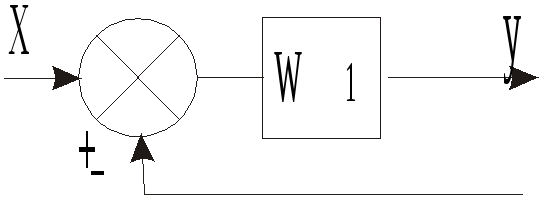
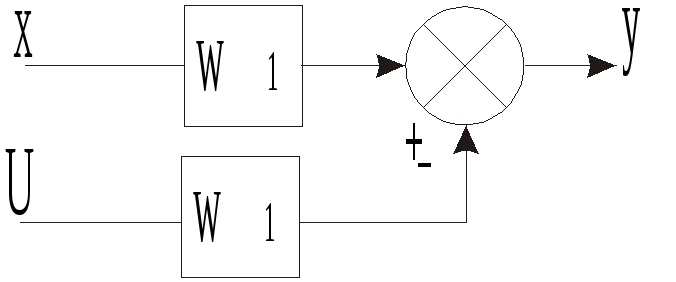
 Перенос
сумматора через элемент
Перенос
сумматора через элемент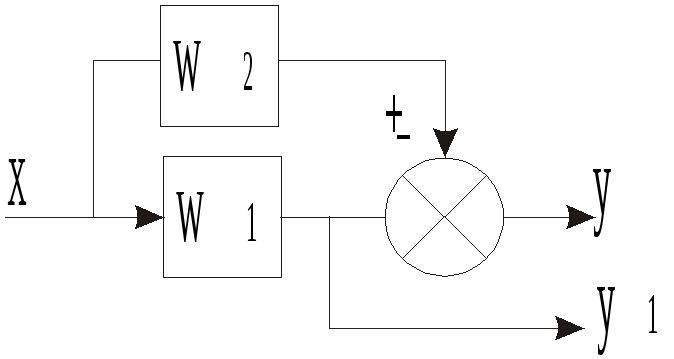
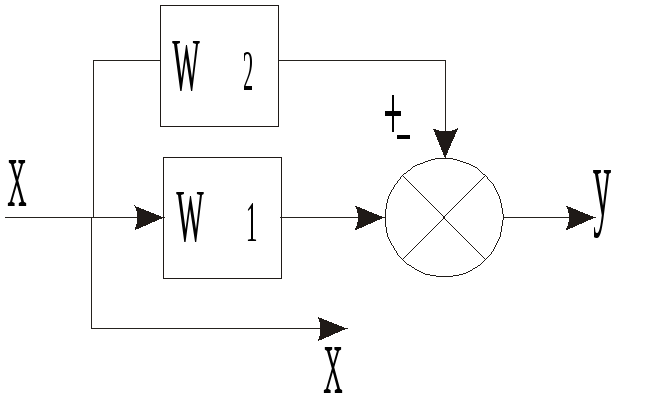
 Вынос
точки разветвления из параллельного
соединения
Вынос
точки разветвления из параллельного
соединения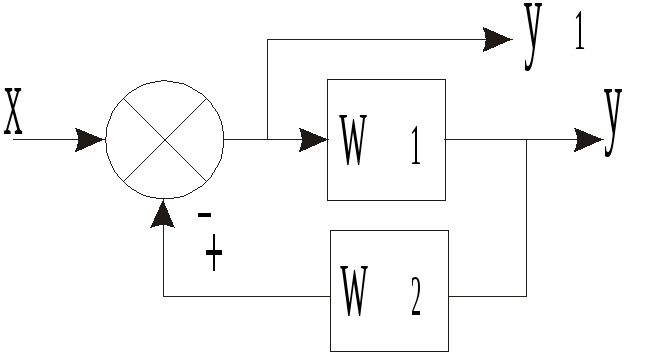
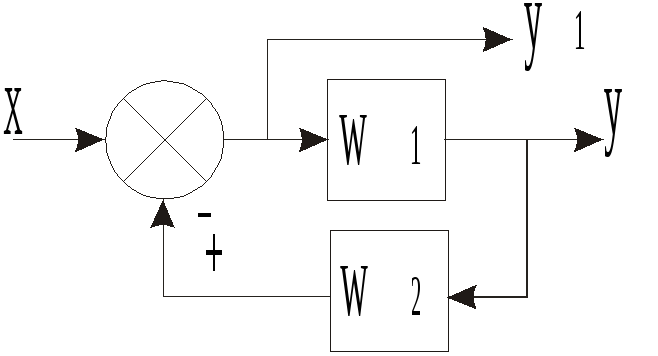
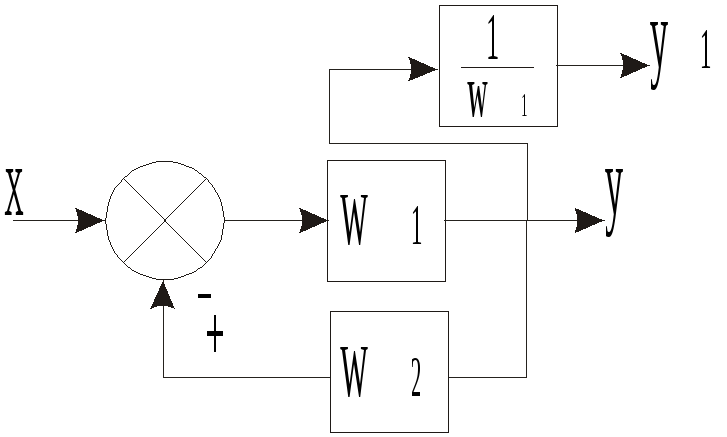
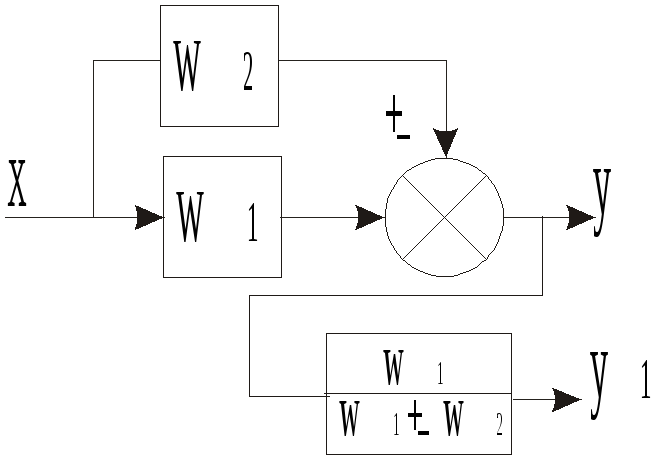
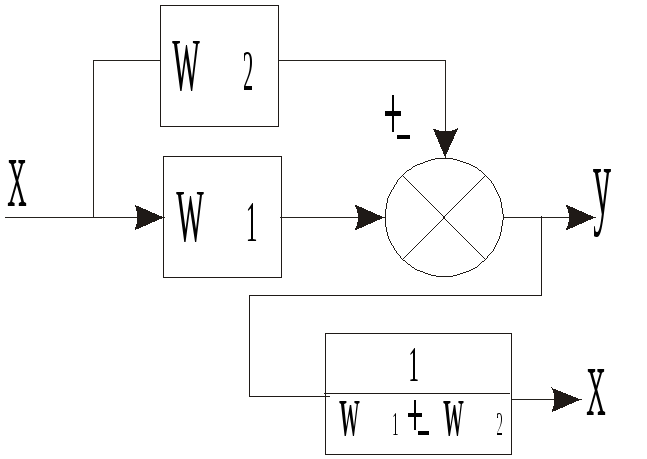
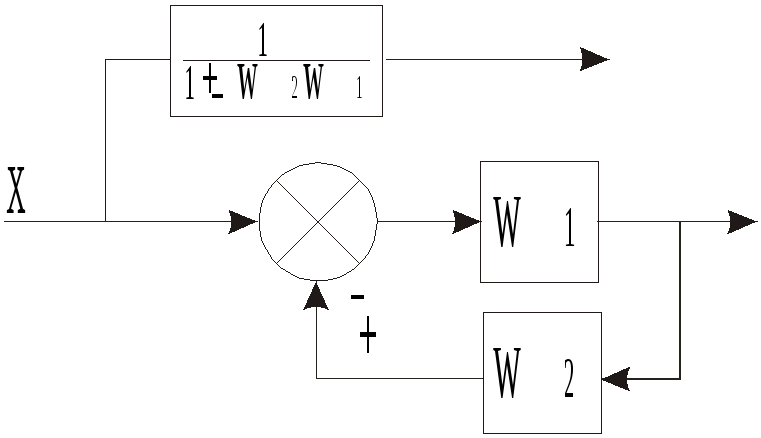 Вынос
точки разветвления из контура обратной
связи
Вынос
точки разветвления из контура обратной
связи