2. Выбор (синтез) типов и параметров регуляторов, обеспечивающих оптимум в системе.

Выбор регуляторов будем производить из условий устойчивости и качества работы САУ как системы с подчиненным регулированием координат [1,3]. Для этого составленную расчетную схему рис.2 эквивалентно преобразуем так, чтобы явно проявлялась структурно подчиненность контуров. Известно, что устойчивость и свободные движения САУ не зависят от входных воздействий [1]. Соответственно выбор регуляторов будем производить при отсутствии возмущения, т.е. при . Тогда расчетная схема САУ примет вид рис.3.

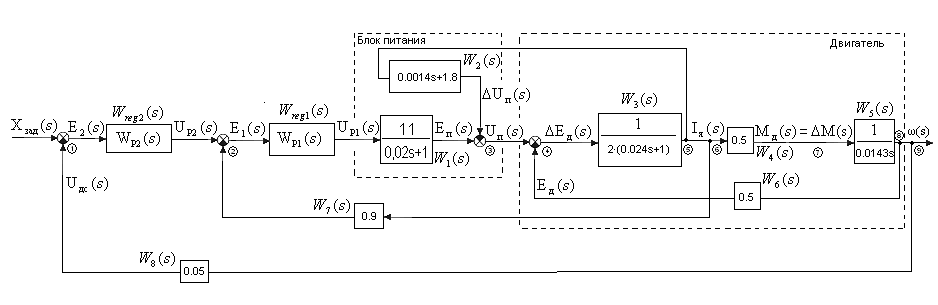Рис.3 Структурная схема САУ при .

Структурная схема САУ рис.3 имеется много пересекающихся связей, упростим топологию этой схемы, производя эквивалентные преобразования [1]. Перенесем эквивалентно сумматор 3 через сумматор 4 в прямом направлении и получим эквивалентную расчетную структурную схему САУ рис.4.

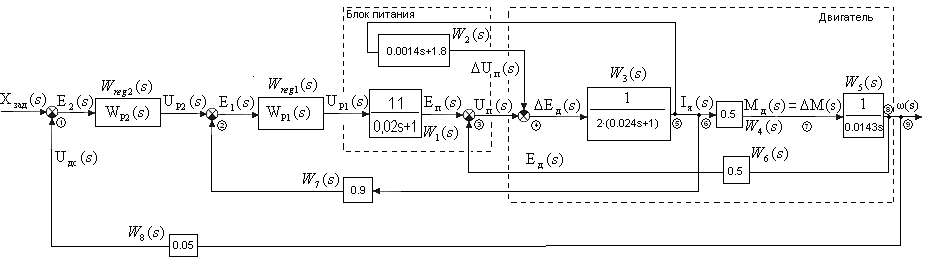
Рис.4 Структурная схема САУ при эквивалентном переносе сумматора 3 чере4 в прямом направлении.

При эквивалентном структурном преобразовании от рис.3 к рис.4 были потеряны физические координаты , . Но анализ схемы рис.4 показывает, что звено охвачено отрицательной обратной связью и для них можно записать эквивалентную общую передаточную функцию . В звене эквивалентно учитываются внутренние параметры двигателя и и внутренние параметры источника питания и , поэтому по эквивалентной структурной схеме рис.5 считаем, что на идеализированный двигатель ( , активное сопротивление и индуктивность преобразователя приведены к двигателю) подается ЭДС , а не напряжение .

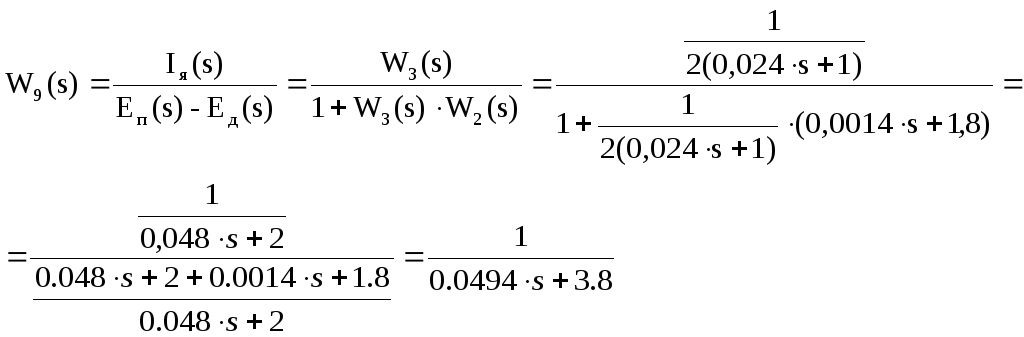
(1)

В результате получится эквивалентная структурная схема рис.5.

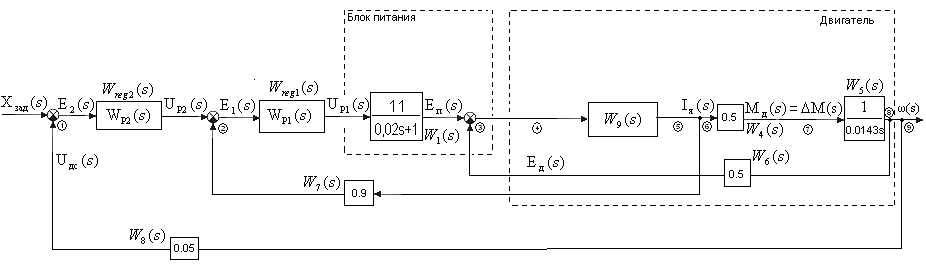
Рис.5 Эквивалентная структурная схема САУ.

В эквивалентной расчетной схеме рис.5 перенесем эквивалентно узел ветвления 8 против направления распространения сигнала в точку 5 и получим новую эквивалентную структурную схему рис.6.

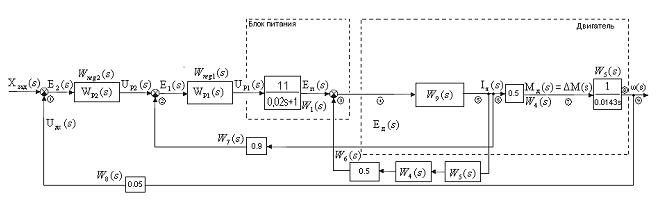
Рис.6 Эквивалентная структурная схема САУ.

Анализ САУ рис.6 показывает, что звено охвачено отрицательной обратной связью из последовательно включенных звеньев . Введем для этой части эквивалентное звено и обозначим его как , его передаточная функция будет равна:

(2)

Знаменатель передаточной функции (2) показывает, что имеется звено второго порядка [1]. Определим это колебательное звено вида если или инерционное звено второго порядка если вида ?

Для этого составим систему алгебраических уравнений приравнивая соответствующие члены:

Решим эту систему алгебраических уравнений.

Произведем подстановку из одного уравнения в другое:

В результате получили алгебраическое уравнение второго порядка относительно .

Решение которого имеет вид:

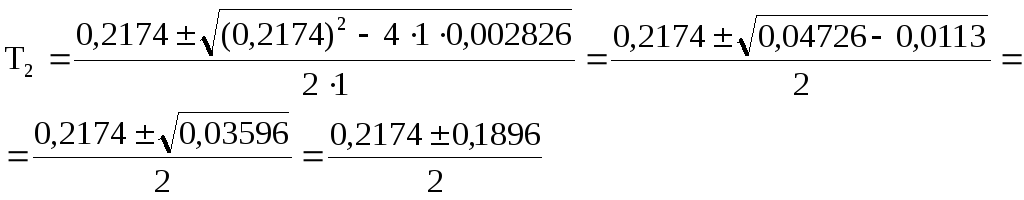
Откуда находим , которые и были подставлены в выражение (2)

После ввода в рис.6 передаточной функции эквивалентная структурная схема САУ примет вид рис.7:

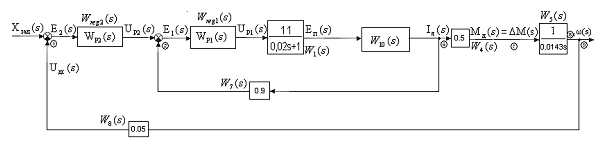
Рис.7 Эквивалентная структурная схема САУ.

Введем новые передаточные функции:

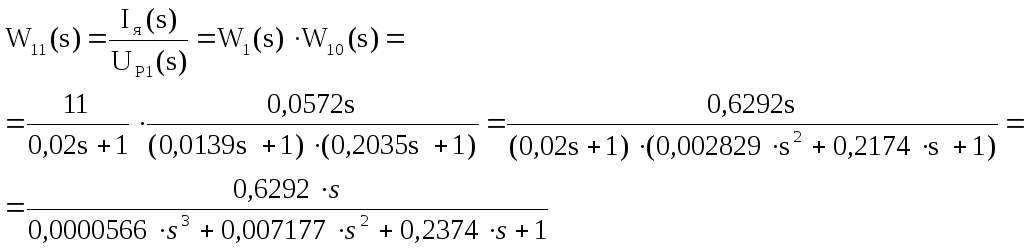(3)

(4)

И получим эквивалентную расчетную схему рис.8, где четко видна подчиненность контуров управления.

Рис.8 Эквивалентная расчетная схема САУ для выбора регуляторов.

По схеме рис.8 и будем выбирать требуемые регуляторы, используя логарифмические частотные методы синтеза корректирующих устройств САУ [1].

Наличие подготовленного материала рис.8 и значений передаточных функций (1÷4) позволяют приступить к синтезу (выбору) структуры и параметров регуляторов. Задача эта трудно формализуемая и, как правило, решается приближено. Воспользуемся методикой синтеза последовательных корректирующих звеньев [1 стр.440÷450] и[3] с методикой осмысленного перебора регулятора до приближения ЛАЧХ разомкнутой системы к желаемой ЛАЧХ.

Известно что по ЛАЧХ разомкнутой системы можно судить о времени переходного процесса замкнутой системы [1] и, следовательно, задаваясь желаемой частотой среза задаём требуемое быстродействие систем. Также же известно, что если желаемая ЛАЧХ проходит через частоту среза под наклоном -20дб/дек не менее чем по полдекады вправо и влево, то в замкнутой системе у переходных процессов перерегулирование будет менее 18% (то есть переходные процессы будут удовлетворительными). Воспользуемся этими сведениями и, изменяя параметры регулятора, будем подгонять ЛАЧХ разомкнутой системы под желаемую.

Строить асимптотические ЛАЧХ типовых звеньев, как известно просто да и ЛФЧХ не представляет сложности строить с использованием номограмм. Но лучше автоматизировать этот процесс с использованием инструментов компьютерных инструментов в среде MatLAB [6].

Следует иметь ввиду следующие соотношения, справедливые для коррекции в нашем случае.

(5)

(6)

Для минимально фазовых систем по ЛАЧХ однозначно определяется ЛФЧХ. Тем не менее для удобства работы одновременно строятся в одном частотном масштабе ЛАЧХ и ЛФЧХ.

Однако в наше время удобнее конечно автоматизировать построение ЛЧХ в инструментах MATLAB раздел Control System Toolbox (CST).

Введем в терминах [3] понятие объекта управления внутреннего контура управления как:

(7)

то есть представим расчетную схему рис.8 в виде эквивалентно схемы рис.9.

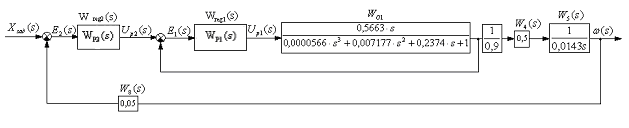
Рис.9 Эквивалентная расчетная схема САУ для выбора первого регулятора.

Задача выбора регулятора значительно упростится, если передаточную функцию объекта управления внутреннего контура упростить, объединяя инерционные звенья с малыми постоянными времени и отбросить (не учитывать) малый коэффициент 0,002829 и получим более простое приближенное выражение первой части объекта. Упрошенное (приближенное) выражение будем отмечать правым индексом _z:

(8)

Естественно и регулятор будем находить тоже приближенно. Асимптотические ЛАЧХ звена (8) построить легко, но мы уже на этом этапе для облегчения синтеза (нахождения) регуляторов воспользовались инструментами CST. Для этого написали программу CVG66-1/

Работу подбора первого регулятора проводил в интерактивном режиме. Задавались приближенной передаточной функцией регулятора , находили приближенную передаточную функцию разомкнутой САУ внутреннего контура , которую методом перебора приближал к желаемой. Окончательный результат показан на рис.10. На ЛАЧХ разомкнутой системы внутреннего контура рис.10 видно, что частота среза достаточно высокая для требуемого быстродействия. Запас по фазе около 100°, а запас по амплитуде теоретически не ограничен.

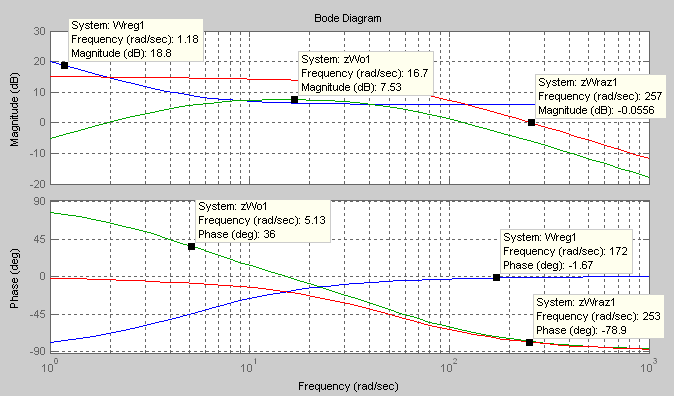
Рис.10 ЛАЧХ и ЛФЧХ внутреннего контура САУ упрощенной системы.

На рис.11 проведены те же расчеты при точном использовании . Ручное (а не компьютерное) построение даже асимптотических ЛАЧХ и ЛФЧХ разомкнутой системы вызвало бы определенные трудности. И хотя было принято упрощение по объекту это не сказалось существенно изменение ЛЧХ.

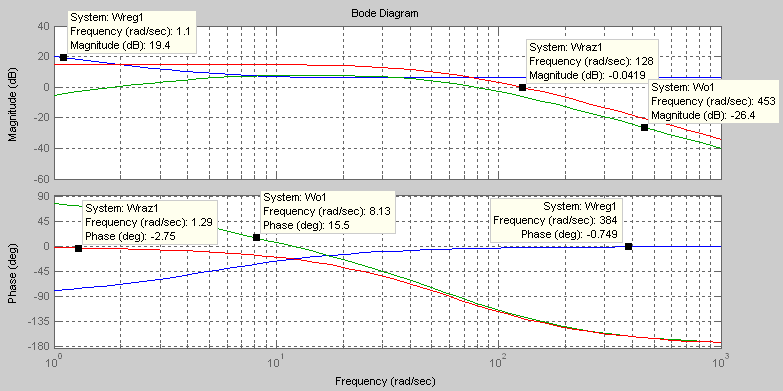
Рис.11 ЛАЧХ и ЛФЧХ внутреннего контура САУ.

Компьютерная поддержка позволила нам сразу построить и переходные функции элементов внутреннего контура управления рис.12. Эти переходные процессы позволяют судить о динамических свойствах (быстродействие) рассматриваемых элементов системы.

Рис.12 Переходные функции элементов внутреннего контура САУ упрощенной системы

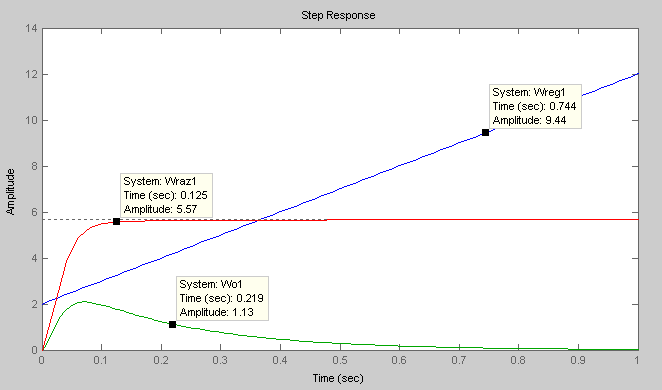Рис.13 Переходные функции элементов внутреннего контура САУ расчетной системы.

В результате был выбран первый регулятор с параметрами:

Выбор первого регулятора (9) позволяет приступить к выбору второго регулятора, а расчетную схему рис.8 представить в виде рис.13.

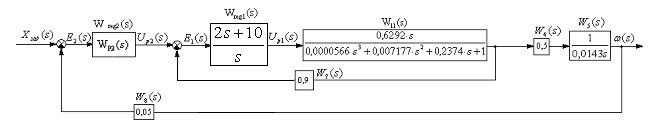
Рис.14 Эквивалентная расчетная схема САУ для выбора второго регулятора.

Структурная схема рис.13 может быть упрощена до вида рис.14. Где введено понятие замкнутой передаточной функции внутреннего контура , в М-файлах будем её обозначать через .

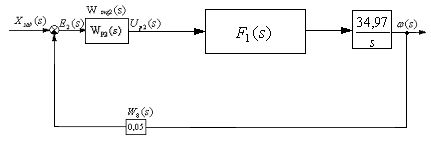
Рис.15 Эквивалентная расчетная схема САУ для выбора второго регулятора.

Звено входит последовательно в цепь при определении частотных характеристик разомкнутой систем внешнего контура. Однако мы не имеем частотных характеристик звена , а имеем частотные характеристики двух видов разомкнутой системы внутреннего контура ЛАЧХ

и ЛФЧХ

Проблема перехода от частотных характеристик разомкнутой системы к частотным характеристикам замкнутой системы очень трудоемка. Можно воспользоваться диаграммами замыкания [1] и построить ЛЧХ замкнутой части внутреннего контура системы, а затем просуммировать их с частотными характеристиками остальных звеньев системы рис.14. Как отмечалось задача эта трудоемкая и мы воспользовались инструментами MATLAB CST и расширили М-файл до программы CVG66-2.

На рис.15 показан окончательный вариант выбора второго регулятора при упрощенном описании объекта управления , когда параметры второго регулятора приняты:

Как видно у разомкнутой системы частота среза , а сдвиг по фазе на этой частоте . То есть имеет место запас по фазе , а запас по амплитуде теоретически равен бесконечности

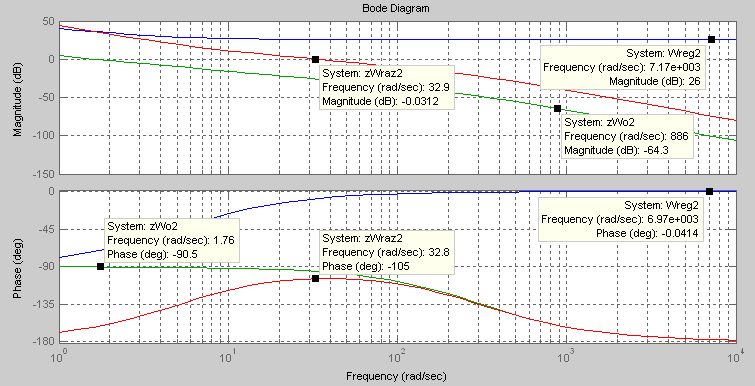
Рис.16 ЛАЧХ и ЛФЧХ внешнего контура САУ упрощенной системы.

В результате выполнения этого пункта предлагается принять регуляторы со следующими параметрами: