
- •Уфимский государственный авиационный технический университет Кафедра атс
- •Уфа-2006
- •Введение
- •Задание на курсовую работу
- •Анализ исходных данных
- •Анализ процесса резания
- •Разработка структурной схемы сар.
- •Анализ устойчивости некорректированной сар.
- •Синтез сар с заданными показателями качества.
- •Анализ качества сар.
- •Замкнутая разработанная сар.
- •Заключение
- •Список литературы
Анализ процесса резания
Анализ процесса резания можно провести следующим образом в несколько этапов:
1. Определение состава выходных координат ПР, в качестве которых можно взять температуру в зоне резания, параметры стружки, силу резания, уровень шероховатости обработанной поверхности, износ инструмента, скорость резания и др.
2. Выбор выходной координаты, наиболее эффективно действующей на процесс резания. За выходную координату возьмём оптимальную температуру в зоне резания, которой соответствует минимальный износ инструмента, максимальное качество ПР и др.
3.
Математическое
описание ОУ:
уравнение (1) отражает
влияние выходной
координаты ![]() от различных
воздействий
от различных
воздействий ![]() ,
,
![]() ,
,![]() :
:
![]() (1)
(1)
4. Определение ограничений, в которых должен действовать ПР. Это ограничение: скорость может регулироваться только вниз от номинальной, т.е. уменьшать входную координату процесса резания.
5.
Определение
состава управляющих координат(УК).
На выходную координату оказывают влияние
глубина резания
![]() ,
подача
,
подача
![]() и скорость
и скорость![]() .
.
6.
Выбор
управляющей координаты
из состава УК, оказывающей наибольшее
влияние на выходную координату. Из
уравнения (1) видно, что скорость эффективно
влияет на температуру резания. Поэтому
управляющая координата –![]() .
.
7.
Определение
состава возмущений.
По условию, на ПР в качестве возмущения
действует изменение величины снимаемого
припуска в пределах
![]() max
–
max
–
![]() min.
Величина V
так же является возмущением, т.к. она
колеблется из-за напряжения сети на
(
min.
Величина V
так же является возмущением, т.к. она
колеблется из-за напряжения сети на
(![]() )Vз
заданного.
)Vз
заданного.
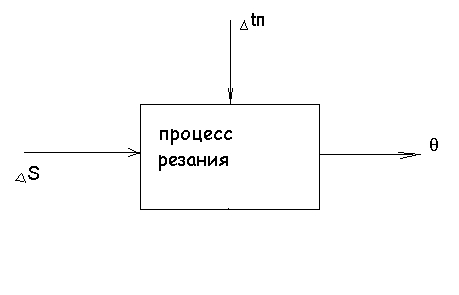 Учитывая
вышесказанное, процесс резания в качестве
объекта управления можно представить
следующим образом:
Учитывая
вышесказанное, процесс резания в качестве
объекта управления можно представить
следующим образом:
8.
Определение
диапазона изменения возмущений.
tп
изменяется в пределах от 1,3 до 1,7 мм.,
т.е. Δ![]() =
0,4 мм;
=
0,4 мм;
V
колеблется на (![]() )Vз
заданного:
)Vз
заданного:
Vmin=Vз – Vzз*0,15=38,25 м/мин;
Vmax= Vз + Vzз*0,1=49,5 м/мин;
ΔV=11.25.

9. Определение отклонения выходной координаты при совместном действии возмущений: температура в зоне резания будет изменяться в пределах:
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]()
![]()
![]() ,
,
![]() %
%
Реальное
отклонение выходной координаты ![]() гораздо больше требуемого
гораздо больше требуемого
![]() 5
5![]() ,
а потому необходим синтез САР выходной
координаты.
,
а потому необходим синтез САР выходной
координаты.
Разработка структурной схемы сар.
Структурную схему составим на основании функциональной схемы и схемы на рис. 1. Структурная схема неизменяемой части САР будет включать в себя все элементы САР, кроме корректирующих устройств.
Преобразователь энергии. С точки зрения динамики процесса ПЭ представляет собой апериодическое звено второго порядка с постоянными времени Т1 и Т2. Его передаточная функция имеет вид:
![]() ,
значения постоянных времени даны в
таблицах, коэффициент
,
значения постоянных времени даны в
таблицах, коэффициент ![]() В,
В, ![]() ,
,
тогда
![]()
ПУ
является линейным звеном. С точки зрения
динамики является апериодическим
звеном первого порядка с постоянной
времени ![]() ,
тогда
,
тогда
![]() ,
где kПУ
=
,
где kПУ
=![]()
По заданию ТПУ = 0, тогда
![]() ,
,
![]()
Датчик обратной связи (ДУ),
![]() ,
где kПУ
=
,
где kПУ
=![]() ,
,![]()
По заданию ТДУ = 0, тогда
![]()
![]() ,
,
![]() .
.
Процесс резания (ПР) описывается уравнением (1):
Зависимость
температуры в зоне резания от подачи
имеет вид при
![]() ,
,
![]() ,
,![]() (1),
(1),

![]() (
(![]() )
)

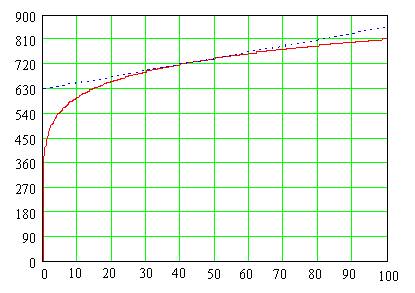 V(м/мин)
V(м/мин)
Рис. 3. Зависимость температуры в зоне резания от скорости
Уравнение
касательной имеет вид:
![]() ,
где
,
где
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() при
V
= 45 м/мин.
при
V
= 45 м/мин.
Линеаризовав
эту зависимость, получим: ![]()
К1=7,6.
Линеаризуем уравнение (1) для получения коэффициента передачи при действии возмущении tп:
![]() ,
,![]()
Уравнение
касательной имеет вид:
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() при
tп
= 1,5 мм .
при
tп
= 1,5 мм .
![]() (
(![]() )
)
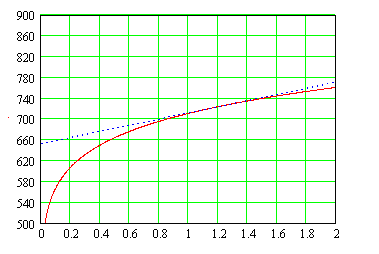 tп
(мм)
tп
(мм)
Рис. 4. Зависимость температуры в зоне резания от глубины резания
Линеаризовав
эту зависимость, получим: ![]() ,
берём K2=
58,5
,
берём K2=
58,5
 Тогда
процесс резания можно представить в
виде следующей схемы:
Тогда
процесс резания можно представить в
виде следующей схемы:
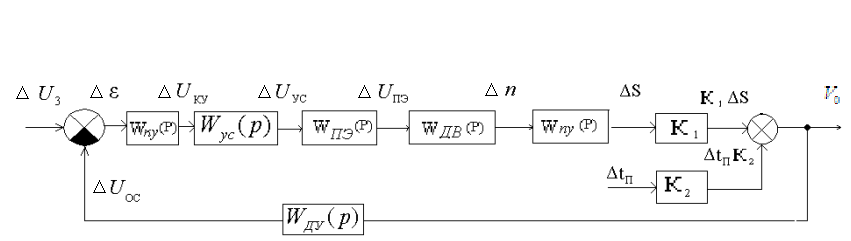
Рис. 5. Структурная схема САР
Двигатель. Электрический двигатель состоит из двух частей: электрической и механической.
 Mc(p)
Mc(p)
U CMФ 1/(JP)

![]()







 I(p)
M(p)
I(p)
M(p) ![]()
CeФ


Рис. 6.Структурная схема двигателя
Уравнение электрического равновесия:
![]()
Уравнения механической части:
![]()
![]() кг·м2,
кг·м2,
![]() А,
А,
![]() =
=![]() рад/с,
рад/с,
![]() В*с/рад,
В*с/рад,
![]() =>
=>
![]() Н·м,
Н·м,
![]() Н·м/А,
Н·м/А,
![]()

![]()
Усилитель УС. Является безинерционным звеном, его передаточную функцию находим из условия:
![]() ,
где ККУ
= 1,
,
где ККУ
= 1,
![]() ,
где
,
где ![]() 5
,
5
, ![]() (
(![]() ), тогда
), тогда
![]() ,
,
![]() .
.


