
- •§ 1. Аффинные системы координат
- •Простое отношение трех точек
- •Задание фигур в пространстве
- •§ 2. Прямая на плоскости Различные виды уравнений прямой на плоскости
- •Угол между прямыми на плоскости
- •Взаимное расположение двух прямых на плоскости
- •Расстояние от точки до прямой
- •§ 3. Уравнения плоскости в пространстве
- •Угол между плоскостями
- •Расстояние от точки до плоскости
- •§ 4. Уравнения прямой в пространстве
- •Взаимное расположение двух прямых в пространстве
- •Общее уравнение прямой в пространстве
- •Расстояние от точки до прямой в пространстве
- •Расстояние между двумя прямыми в пространстве
- •Взаимное расположение прямой и плоскости
- •Угол между прямой и плоскостью
- •§ 5. Полярная система координат
- •Обобщенные полярные координаты
- •Решение нулевого варианта контрольной работы
- •Список литературы
- •305000, Г. Курск, ул. Радищева, 33
Расстояние от точки до плоскости
Пусть плоскость p задана общим уравнением в О :
p: = 0
Нормальный
вектор плоскости имеет координаты:
.
Выберем произвольно точку М0(![]() )
и найдем расстояние от точки М0
до плоскости p.
Из точки М0
опустим
перпендикуляр на плоскость p
и обозначим основание перпендикуляра
М1(
)
и найдем расстояние от точки М0
до плоскости p.
Из точки М0
опустим
перпендикуляр на плоскость p
и обозначим основание перпендикуляра
М1(![]() ).
).
Так
как М1Îp,
то
![]() = 0
= 0
и
D
= –(
+![]() ).
(9)
).
(9)
Искомое расстояние равно |М1М0|. С другой стороны || и, следовательно, угол j между ними равен или 0 или p. Поэтому:
(
,
)
= |
1|×
|
|×cosj
= ±|
|×
|
|
= ±|
|×![]() .
.
Очевидно,
(![]() .
.
Поэтому, учитывая (9), получим:
(
,
)
=
+
![]() =
=
=
=![]() =
=![]() .
.
Чтобы избавиться от знаков ±, будем рассматривать выражения по абсолютной величине. Получим:
| |× = | |,
(М0,
)
= |М1М0|
=
![]() .
(10)
.
(10)
Замечание. Пусть даны две параллельные плоскости. Тогда можно рассматривать расстояние между этими плоскостями. Найти это расстояние можно как расстояние от любой точки одной плоскости до другой плоскости.
Знак четырехчленна Ах+Ву+Сz+D
Пусть плоскость p задана общим уравнением в О :
p: = 0
Нормальный
вектор плоскости имеет координаты:
.
От произвольной точки М0(
)
плоскости p
откладываем представитель
![]() вектора
,
М1(
).
Пусть
плоскость p
разбивает пространство на два открытых
полупространства, которые обозначим a
и b,
причем полупространство a
содержит отрезок
.
Тогда, как нетрудно заметить, если точка
М(
вектора
,
М1(
).
Пусть
плоскость p
разбивает пространство на два открытых
полупространства, которые обозначим a
и b,
причем полупространство a
содержит отрезок
.
Тогда, как нетрудно заметить, если точка
М(![]() )
расположена в полупространстве a,
то угол между векторами
и
будет острый. Если точка М
расположена в полупространстве b,
то угол между векторами
и
будет тупой. Рассматривая скалярные
произведения этих векторов, получим:
)
расположена в полупространстве a,
то угол между векторами
и
будет острый. Если точка М
расположена в полупространстве b,
то угол между векторами
и
будет тупой. Рассматривая скалярные
произведения этих векторов, получим:
Если точка М расположена в полупространстве a, то ( , ) > 0.
Если точка М расположена в полупространства b, то ( , ) < 0.
Записывая 1 и 2 в координатной форме получим:
М
Î
a
Û![]() >
0,
>
0,
М Î b Û < 0,
Учитывая, что точка М0Î p, (см (9)) получим:
М
Î
a
Û![]() > 0,
(11)
> 0,
(11)
М Î b Û < 0. (12)
Таким образом, строгие неравенства (11), (12) являются уравнениями открытых полупространств. Если неравенства нестрогие, т.е.
≥ 0, (13)
£ 0. (14),
то они являются уравнениями полупространств (вместе с граничной плоскостью p).
Пример. Заданы четыре точки в прямоугольной декартовой системе координат: А(-1; 2; 3), В(2; -2; 3), С(-1; 4; 5), D(-1; 6; 0).
(А, В, С, D – вершины тетраэдра).
1. Составить уравнение всех плоскостей, содержащих грани тетраэдра.
2. Найти косинус угла между плоскостями (АВС) и (АВD).
3. Найти длину высоты тетраэдра, проведенную из вершины D.
4. Составить уравнение плоскости, проходящей через точку D и перпендикулярно прямой (BD).
Записать систему неравенств, задающих внутреннюю область тетраэдра ABCD.
Решение.
Плоскость (АВС) можно задать точкой А(-1; 2; 3) и векторами
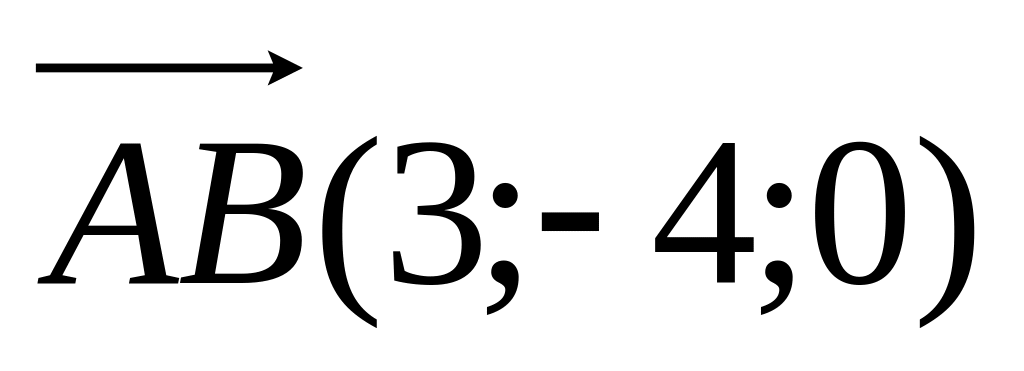 ,
,
 .
.
Поэтому ее параметрические уравнения будут иметь следующий вид:

Запишем уравнение плоскости в форме определителя
 (1)
(1)
Разложив определитель по первой строке, получим общее уравнение плоскости (ABC):
![]()
![]() .
.
Аналогично можно получить общие уравнения плоскостей оставшихся граней тетраэдра, а именно:
(ABD): 4x + 3y + 4z − 14 = 0,
(ACD): x + 1 = 0,
(BCD): 34x + 15y + 6z – 56 = 0.
Обозначим - острый двугранный угол между плоскостями (АВС) и (ABD). (
 ,
где
,
где
 - нормальные вектора, соответственно,
плоскостей (АВС)
и (ABD).
Так как
- нормальные вектора, соответственно,
плоскостей (АВС)
и (ABD).
Так как
 или
или
 ,
то
,
то
 .
.
Из общих уравнений данных плоскостей имеем:
![]() и
и
![]() .
.
Тогда
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Таким
образом, косинус угла между плоскостями
(АВС)
и (ABD)
равен
![]()
3. Длину высоты тетраэдра, проведенную из вершины D(-1; 6; 0) можно вычислить как расстояние от точки D до плоскости (АВС): .
![]() ,
,
где |DH| - искомая высота.
Учитывая,
что
![]() ,
,
где А, В, С, D – коэффициенты общего уравнения плоскости (АВС), а x0, y0, z0 – координаты точки D, найдем искомую высоту:
![]() .
.
4.
По условию вектор
![]() (–3;
8; –3) является
нормальным вектором искомой плоскости.
Поэтому ее можно задать точкой D(–1;
6; 0) и нормальным
вектором
(–3;
8; –3) является
нормальным вектором искомой плоскости.
Поэтому ее можно задать точкой D(–1;
6; 0) и нормальным
вектором
![]() ,
а значит можно воспользоваться известным
уравнением:
,
а значит можно воспользоваться известным
уравнением:
A(x – x0) + B(y – y0) + C(z– z0)=0,
где А, В, С – координаты нормального вектора плоскости;
x0, y0, z0 – координаты точки, принадлежащей плоскости.
Подставив в данное уравнение, получим:
–3(x
+ 1) + 8(y
– 6) – 3z
= 0
![]() 3x
– 8y
+ 3z
+ 51=0.
3x
– 8y
+ 3z
+ 51=0.
5. Внутреннюю область тетраэдра можно задать как пересечение открытых полупространств, определяемых плоскостями граней тетраэдра и содержащих рассматриваемый тетраэдр. Для этого нам необходимо иметь уравнения этих плоскостей (эти уравнения были получены ранее):
(ABD): 4x + 3y + 4z − 14 = 0,
(ACD): x + 1 = 0,
(BCD): 34x + 15y + 6z – 56 = 0,
(АВС): 4х+ 3у -3z +7= 0.
Чтобы определить необходимое полупространство, заданное, например, плоскостью (АВС), мы выясним знак четырехчлена 4х+ 3у -3z +7 при подстановке координат точки D(-1; 6; 0) :
4∙ (-1)+3∙6 - 3∙0 + 7=21>0.
Таким образом, уравнением необходимого полупространства будет неравенство: 4х+ 3у -3z +7 > 0.
Аналогично мы находим уравнения остальных открытых полупространств, содержащих данный тетраэдр: 34x + 15y + 6z – 56 < 0, x + 1 > 0, 4x + 3y + 4z − 14 >0.
Следовательно, внутренняя область тетраэдра будет задаваться следующей системой неравенств:
![]()
