Задание фигур в пространстве
Пусть в пространстве введена система координат Охуz. Как мы показали, положение любой точки однозначно определяется ее координатами. Если Ф – некоторое множество точек ( фигура ), то всем ее точкам характерно некоторое свойство, присущее только точкам этой фигуры, а значит и для координат точек этой фигуры выполняется соотношение, присущее только точкам этой фигуры.
Определение. Пусть в данной системе координат имеем некоторое уравнение
F (x, y, z) = 0. (1)
Уравнение (1) называется уравнением фигуры Ф, если координаты любой точки этой фигуры, и только они, удовлетворяют этому уравнению.
Следует
добавить, что уравнение (1) будет уравнением
фигуры Ф,
если выполняются два условия: 1) Если
М(
)
Ф, то координаты
(
)
удовлетворяют (1); 2) Если координаты (
)
удовлетворяют уравнению (1), то М(
)
Ф.
Под уравнением фигуры мы понимаем не только алгебраические уравнения, но и неравенства, системы уравнений и неравенств, а также их любые комбинации. Например, неравенство
(х –- )2 +(у – )2 + (z – )2 R2
является уравнением шара с центром в точке Q(; ; ) и радиусом R.
Аналогично определяется уравнение фигуры на плоскости, только в системе координат Оху.
Уравнение
является уравнением точек первой
четверти, причем точки, лежащие на осях
координат, не принадлежат данному
множеству.
Пример 1. Центр О и вершина А правильного шестиугольника ABCDEF имеют координаты О(–1; 2), А(1; 4). Найти координаты остальных вершин.
Решение. Так как точка О является серединой отрезка АD, то находим координаты точки D. Обозначим D(х; у), тогда согласно (3) имеем:
,
.
Отсюда получим: х = – 3, у = 0. D(-3; 0).
Так как данный шестиугольник правильный, то АВО и AFO – правильные треугольники. Значит, точки В и F являются точками, равноудаленные от точек А и О. Пусть В(х; у). Из условия |AB| = |OB| = |OA| получим |AВ|2 = |ОB|2 = |ОА|2. В координатной форме это выглядит так:
Û
Следовательно,
B(
;3-
)
и
F
(–
;
3 +
).
Так как точки Е и С симметричны точкам В и F относительно точки О, то находим их координаты аналогично тому, как мы находили координаты точки D. Обозначим Е(х; у), тогда согласно (3) имеем:
,
.
Отсюда получим: х = – ( +2), у = 1+ . Е(-( +2);1+ ).
Обозначим С(х; у), тогда согласно (3) имеем:
,
.
Отсюда получим: х = -2, у = 1- . С( -2; 1- ).
Ответ: С( -2; 1- ), Е(-( +2);1+ ), B( ;3- ), F (– ; 3 + ), D(– 3;0).
Пример 2. Найти уравнение множества всех точек плоскости, для каждой из которых сумма квадратов расстояний до осей координат равна 5.
Решение.
Рассматриваем систему координат О
.
Обозначим заданное множество точек
F,
а М (х; у)
– произвольную точку плоскости.
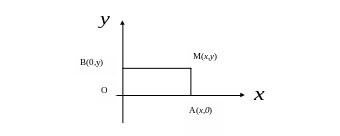
Тогда, согласно условию задачи, получим
М F |MB|2 + |MA|2 = 5.
В координатах последнее уравнение имеет вид
х2+ у2 = 5.
Получили
известное уравнение окружности с центром
в начале координат и радиусом равным
.