Трех уровнях цен на товар

Рассмотрим математическое описание модели блочного ценообразования для осуществления ценовой дискриминации второй степени.

Пусть спрос на продукцию фирмы-монополиста описывается функцией P = P(Q), а совокупные затраты TC = TC(Q). Обозначим через q₁ объем первой партии, через q₂ - второй, через q_i - количество единиц продукции в i - ой партии и положим, что производитель делит весь объем продукции на k партий. Согласно функции спроса цена каждой единицы первой партии р₁ = Р( q₁ ). Цена каждой единицы второй партии зависит от q₂ и q₁ : p₂ = P(q₁ + q₂ ). Цена каждой единицы третьей партии р₃ зависит от q₃ и от q₂ и q₁ : p₃ = P(q₁ + q₂ + q₃ ). Продолжив аналогичные рассуждения , можно получить следующие соотношения:

р₁(q₁) = Р( Q₁ ) , где Q₁ = q₁ ,

р₂(q₂) = Р( Q₂ ) , где Q₂ = q₁ + q₂ ,

… … … (8.6)

р_i(q_i) = Р( Q_i ) , где Q_i = q₁ + q₂ + … + q_i ,

… … …

р_k(q_k) = Р( Q_k ) , где Q_k = q₁ + q₂ + … + q_i … + q_k .

Сформулируем задачу максимизации прибыли фирмы в условиях ценовой дискриминации второй степени.

П(Q_k)={TR(q₁) + TR(q₂) +…+ TR(q_i) +…+ TR(q_k)} - TC(q₁ + q₂ +…+ q_i +…+q_k)  max (8.7)

или

П(Q_k) = {q₁Р(Q₁) + q₂ Р(Q₂) +…+ q_i Р(Q_i) +…+ q_k Р(Q_k)} - TC(Q_k)  max (8.8)

Согласно необходимому условию определения максимума функции k переменных имеем:

… … … … …

… … … …

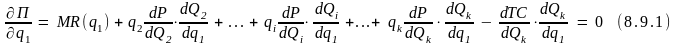
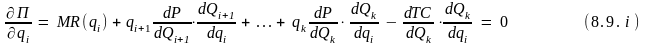
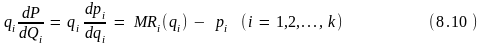Учитывая (8.6), получаем, что dQj/dq_j = 1 (i, j = 1,2, … , k ). Кроме того, легко видеть, что

Тогда, с учетом (8.10), равенства (8.9.1) - (8.9.k) можно переписать в следующем виде:

MR₁ + MR₂ - P₂ + … + MR_i - p_i + … + MR_k - p_k - MC = 0 (8.11.1)

MR₂ + MR₃ - P₃ +… + MR_i - p_i + …+ MR_k - p_k - MC = 0 (8.11.2)

… … … …

MRi + MR_i+1 - p_i+1 + …+ MR_k - p_k - MC = 0 (8.11.i)

… … … …

MR_k - MC = 0 (8.11.k)

Складывая попарно выражения (8.11.1) и (8.11.2), (8.11.2) и (8.11.3) и т.д. (8.11.i) и 8.11.i+1), и, наконец, (8.11.k-1) и (8.11.k), которые являются тождествами для значений qi ( i = 1,2, … , k), при которых прибыль фирмы максимальна, получаем условие первого порядка для максимума функции прибыли (8.7) - (8.8) в следующей форме.

MR(q₁) = p₂ ,

MR(q₂) = p₃ ,

… … (8.12)

MR(q_i) = p_i ,

… …

MR(q_k) = MC(Q_k) .

Следовательно, для получения максимальной прибыли при осуществления ценовой дискриминации второй степени цены должны назначаться согласно правилу (8.12), которое можно назвать правилом оптимального ценообразования. Оно говорит о том, что для того, чтобы получить максимальную прибыль, фирма должна устанавливать цену для каждой единицы i – ой партии на уровне предельной выручки от продажи предшествующей партии продукции.

Приведем графическую иллюстрацию данного правила для линейной функции спроса. На рисунке 8.13 изображены обратная функция спроса P = 100 - Q, МC(Q) – функция предельных издержек фирмы-монополиста.

100 P(Q)

А

p₁ = 80

B

p₂ = 60 m

p^m g

C

p₃ = 40

p^c h

20 g MC

e d

F

20 40 60 MR₃ 100 Q

Q_m MR₁ MR₂

Рис. 8.13. Применение правила оптимального ценообразования

для трех уровней цен

Допустим, монополист делит всю продукцию на три партии, то есть k = 3, и устанавливает размер первой партии, равный 20 единицам. Обозначим через Q_к = ∑q_к , где q_к - размер к - ой партии товара.

Тогда выполняются следующие выражения для цен:

р₁ = Р(Q₁) = P(q₁) = 100 - q₁ = 100 - 20 = 80, (8.13)

р₂ = Р(Q₂) = P(q₁ + q₂) = (100 - q₁) - q₂ = 80 - q₂ для q > q₁ = 20. (8.14)

Для того, чтобы определить размер второй партии применим условие оптимальности (8.12). Оценим MR₁(q₁). Согласно (8.13) MR₁ = 100 - 2q₁ = 100 - 40 = 60. Следовательно р₂ = 60, тогда q₂ = 20.

Определим р₃ . Согласно (8.12) р₃ = MR₂ (q₂ ) = 80 - 2q₂ = 80 – 40 = 40.

Так как р₃ = P(Q₃) = 100 - (q₁ + q₂ + q₃) = (100 - 40) - q₃ = 60 - q₃ для q > (q₁ + q₂) = 40, то q₃ = 60 - р₃ = 20. Используя последнее из соотношений (8.12), находим, что

МС(Q₃) = MC(q₁ + q₂ + q₃) = МС(60).

МС (q₃) = MR₃ (q₃) = 60 - 2q₃ = 60 – 40 = 20.

На рисунке 8.13 хорошо видно, что применение схемы блочного ценообразования позволяет монополисту значительно увеличить прибыль по сравнению с той, которую обеспечивает стратегия оптимального монопольного ценообразования (MR₁ = MC), и завладеть существенной частью излишка потребителя, соответствующего конкурентной схеме ценообразования ( p = MC = p^c). Действительно, сумма площадей прямоугольников А, В, С и четырехугольника F,p^c,h,d равна совокупной прибыли фирмы в условиях дискриминации. Она намного превышает прибыль фирмы, которую обеспечивает стратегия оптимального монопольного ценообразования (площадь четырехугольника F,p^m,m,e).

При конкурентной схеме ценообразования прибыль фирмы определяется площадью треугольника F,p^c,g, и совпадает с излишком производителя. Величина излишка потребителя измеряется площадью треугольника p^c,100,g. На рисунке 8.13 большая часть площади этого треугольника представлена суммой площадей прямоугольников А, В и С. Площадь А + В + С отражает ту часть излишка потребителя, которая стала весомой добавкой к прибыли производителя в условиях ценовой дискриминации.

Покажем, что для линейной функции спроса максимальная прибыль в условиях блочной схемы ценообразования достигается при равных размерах партий товара. Допустим, обратная функция спроса P = a – bQ (a > 0, b > 0), TC(Q) – функция совокупных издержек (Q = q₁ + q₂ + … + q_i … + q_k , k = 2, …, n ). По аналогии с (8.6), опишем зависимость каждой из назначаемых цен p_k от размера предыдущих партий продукции.

р₁ = P(q₁) = a - bq₁ ,

р₂ = P(q₁ + q₂) = a - b(q₁ + q₂) = (a - bq₁) - bq₂ ,

… … … (8.15)

р_i = P(q₁ + q₂ +…+ q_i ) = a - b (q₁ + q₂ +…+ q_i ) = [a - b (q₁ + q₂ +…+ q _i-1)] - bq_i ,

… … …

р_k = P(q₁ + q₂ +…+ q_i +… + q_k ) = a - b(q₁ + q₂ +…+ q_i +…+ q_k) =

= [a - b (q₁ + q₂ +…+ q _k-1)] - bq_k .

Сформулируем задачу максимизации прибыли фирмы.

П(q₁ + q₂ +…+ q_i +…+ q_k) = q₁p₁ + q₂p₂ +…+ q_ip_i +…+ q_kp_k = q₁(a - bq₁ ) + q₂[(a - bq₁) - bq₂] + … + q_i [a - b (q₁ + q₂ +…+ q _i-1) - bq_i ] +… + q_k [a - b (q₁ + q₂ +…+ q _k-1) - bq_k ] -

• TC (q₁ + q₂ +…+ q_i +…+ q_k)  max (8.16)