
- •1. Закон Кулона. Закон сохранения заряда. Принцип суперпозиции.
- •2. Электростатическое поле (напряженность электростатического поля, поле точечного покоящегося электрического заряда, потенциальность поля)
- •3. Основная задача электростатики (для точечных зарядов в вакууме, для произвольного объемного, поверхностного и линейного распределения зарядов)
- •4. Дифференциальные операторы (оператора (набла), дивергенция функции divF, ротор функции rotF)
- •5. Безвихревой характер электростатического поля
- •6. Поток вектора напряженности
- •7. Теорема Гаусса (в том числе - для точечного заряда)
- •8. Применение теоремы Гаусса для расчета полей - поле бесконечной, прямой, равномерно заряженной нити
- •9. Применение теоремы Гаусса для расчета полей - поле бесконечной, равномерно заряженной плоскости
- •10. Применение теоремы Гаусса для расчета полей - поле сферической, равномерно заряженной поверхности
- •11. Теорема Гаусса в дифференциальной форме (вакуум).
- •12. Уравнение Пуассона (вакуум).
- •13. Плотность заряда для точечного заряда (δ-функция).
- •14. Поле Диполя.
- •15. Диэлектрики и вектор поляризации.
- •16. Основная задача электростатики для поля в диэлектрике (истинные и связанные заряды).
- •17. Уравнение Пуассона для поля в диэлектрике.
- •19. Теорема Гаусса для поля в диэлектрике (интегральная форма).
- •20. Закон Кулона в диэлектрике (Теорема Гаусса для поля в диэлектрике).
- •21. Свойства проводников
- •22. Метод изображений (для бесконечно проводящей плоскости и сферы)
- •23. Электроемкость уединенного проводника
- •24. Конденсатор – Сферический конденсатор
- •25. Конденсатор – Плоский конденсатор
- •26. Конденсатор – Соединения конденсаторов
- •27. Энергия заряженного проводника
- •28. Энергия электростатического поля
- •29. Ток и плотность тока
- •1. Работа тока (вдоль произвольного контура, мощность и удельная мощность тока)
- •2. Интегральные закона Ома (для участка цепи, содержащего эдс - определение эдс и сопротивления участка цепи; для замкнутого проводника; для участка цепи не содержащего эдс)
- •3. Закон Ома в дифференциальной форме.
- •4. Тепловое действие тока (закон Джоуля-Ленца в дифференциальной и интегральной формах)
- •5. Правила Кирхгофа.
- •6 . Постулат Ампера
- •7. Закон Био-Савара-Лапласса
- •8. Силовое действие магнитного поля – закон Ампера
- •9. Закон Ампера: сила Лоренца, сила Ампера
- •10. Силовое действие магнитного поля – принцип действия электромотора
- •11. Силовое действие магнитного поля – принцип действия электромотора.
- •12. Калибровочная инвариантность магнитного поля
- •13. Применение закона бсл для расчета магнитных полей – поле бесконечного, прямого проводника с постоянным током.
- •14. Применение закона бсл для расчета магнитных полей – поле кругового проводника с постоянным током.
- •15. Закон полного тока – уравнение Пуассона для магнитного поля.
- •16. Закон полного тока (в дифференциальной и интегральной формах)
- •17. Применение закона полного тока для расчета магнитных полей – поле бесконечного, прямого проводника с постоянным током.
- •18. Применение закона полного тока для расчета магнитных полей – поле бесконечного соленоида с постоянным током.
- •19. Теорема Гаусса для магнитного поля.
- •20. Магнитный момент.
- •21. Магнитная восприимчивость
- •22. Закон полного тока для магнитного поля в магнетике
- •23. Уравнение Пуассона для магнитного поля в магнетике
- •24. Векторный потенциал магнитного поля в магнитной среде
- •25. Типы магнетизма (Суперпарамагнетизм, Антиферромагнетизм (Клапаны вращения), Ферримагнетизм, Ферромагнетизм (Ферромагнитные материалы), Парамагнетизм, Диамагнетизм)
- •26. Магнетизм вещества.
24. Конденсатор – Сферический конденсатор
Р ассмотрим
два электрически нейтральных проводника,
находящихся внутри однородной изотропной
среды с диэлектрической проницаемостью
ассмотрим
два электрически нейтральных проводника,
находящихся внутри однородной изотропной
среды с диэлектрической проницаемостью
Перенесем заряд +q с одного проводника на другой
Способность
системы нейтральных проводников изменять
свой потенциал в результате переноса
заряда с одного проводника на другой
называют взаимной емкостью С проводников
![]()
Соответственно, любую систему двух проводников называют конденсатором
При этом, если проводники нейтральны, то говорят, что конденсатор не заряжен – процесс переноса заряда с одного проводника на другой называют зарядкой конденсатора
Сферический конденсатор
Р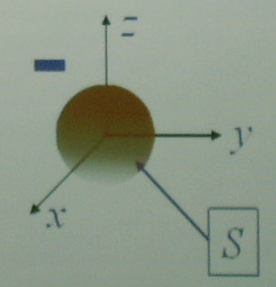 ассмотрим
нейтральный проводник сферической
формы – чтобы зарядить такой конденсатор
нужно перенести заряд (например +q)
с его поверхности на бесконечность
ассмотрим
нейтральный проводник сферической
формы – чтобы зарядить такой конденсатор
нужно перенести заряд (например +q)
с его поверхности на бесконечность
Следовательно
сферический конденсатор имеет емкость
единенного проводника и т.е.
![]()
Найдем емкость уединенного сферического проводника
По определению (в выбранной СК)
![]()

Т.к.
проводник сферический, то |r’|=R,
где R
– радиус сферы, причем поверхностная
плотность заряда
![]() на
сфере
на
сфере
![]()
Таким
образом
![]()
Получаем,
что электроемкость сферического
конденсатора равна
![]() ,
где
,
где
![]()
Электроемкость сферического конденсатора пропорциональна его радиусу
25. Конденсатор – Плоский конденсатор
Рассмотрим
систему из двух нейтральных проводящих
бесконечных плоскостей, находящихся
на расстоянии d
– чтобы зарядить такой конденсатор
нужно перенести заряд (например +q)
с одной его плоскости на другую. Очевидно,
что электроемкость плоского конденсатора
![]()
В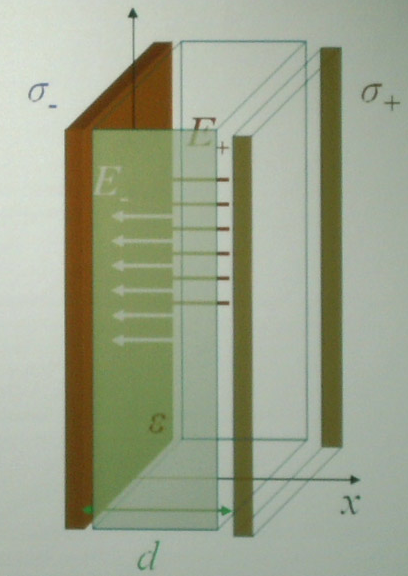 результате зарядки на плоскостях
появится поверхностная плотность
зарядов (одинаковая по величине)
результате зарядки на плоскостях
появится поверхностная плотность
зарядов (одинаковая по величине)
Соответственно,
каждая плоскость создаст свое
электростатическое поле E+
и
E-.
В результате, поле вне конденсатора
компенсируется. Напряженность поля
внутри – складывается и, если внутри
находится диэлектрик, то
![]()
Зная
напряженность, можно найти разность
потенциалов между пластинами конденсатора
![]()
![]()
По
определению взаимной емкости
![]()
![]()
26. Конденсатор – Соединения конденсаторов
Конденсаторы являются одними из основных элементов электрических цепей – как и все элементы, их можно соединять параллельно:
![]()
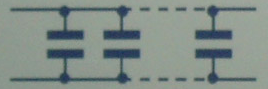
И последовательно:
![]()
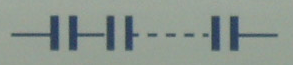
Здесь: i – номер конденсатора, n – общее количество соединенных конденсаторов
27. Энергия заряженного проводника
Элементарная
работа, совершаемая электростатическим
полем на элементарном перемещении
заряда q
равна
![]()
Следовательно,
работа против сил поля
![]()
Найдем
работу, которую нужно совершить, чтобы
зарядить уединенный проводник до
потенциала
![]()

Тогда
для произвольного количества проводников
![]()
По
физическому смыслу работа, проведенная
над любым телом, есть его потенциальная
энергия, т.е.
![]() электростатическая энергия заряженного
проводника, где
-
поверхностная плотность заряда на
проводнике
электростатическая энергия заряженного
проводника, где
-
поверхностная плотность заряда на
проводнике
28. Энергия электростатического поля
Электростатическая энергия заряженного проводника – это энергия зарядов, перенесенных на проводник – следовательно, эта энергия численно равна энергии электростатического поля перенесенных зарядов
Преобразуем
формулу
![]() так, чтобы она описывала энергию поля
через характеристики поля
так, чтобы она описывала энергию поля
через характеристики поля

![]()
![]()

![]() -
энергия электростатического поля в
объеме V
-
энергия электростатического поля в
объеме V
Величину
![]() называют объемной плотностью энергии
электростатического поля
называют объемной плотностью энергии
электростатического поля
