20. Закон Кулона в диэлектрике (Теорема Гаусса для поля в диэлектрике).

Электростатическое поле всегда потенциально:

Следовательно, уравнение Пуассона можно записать в виде:

Введём вектор электрического смещения электрического поля:

Таким образом, мы получаем теорему Гаусса в дифференциальной форме для электростатического поля в диэлектрике:

Дивергенция вектора электрического смещения электростатического поля в любой точке пространства пропорциональна плотности истинных зарядов в этой точке.

Вектор электрического смещения электростатического поля называют также вектором индукции электростатического поля.

21. Свойства проводников

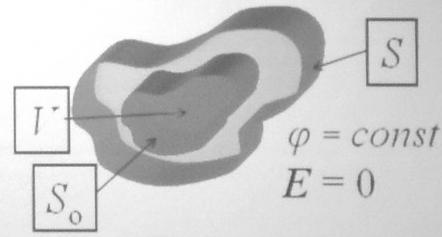
Проводником будем называть любое тело, все точки которого в стационарных условиях и в отсутствии внешних электрических полей имеют одинаковый потенциал

Следовательно, напряженность электрического поля внутри проводника равна нулю

Из теоремы Гаусса , (где S₀-произвольная замкнутая поверхность внутри проводника, охватывающая объем V; S-поверхность проводника) следует, что внутри проводника зарядов нет → заряды распределяются только по поверхности проводника.

Если внести проводник во внешнее электростатическое поле, то заряды на поверхности перераспределяются таким образом, чтобы поверхность (и весь объем) проводника осталась эквипотенциальной → всегда (в поле и вне)

22. Метод изображений (для бесконечно проводящей плоскости и сферы)

О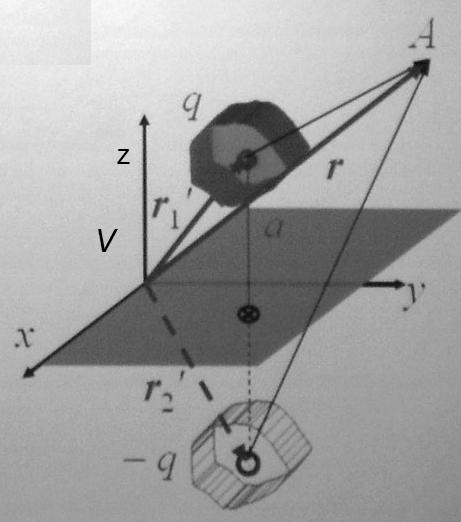 сновное свойство проводников позволяет иногда значительно упростить задачу вычисления электростатического поля, создаваемого зарядами, расположенными около проводящих поверхностей.

Пусть точечный заряд q, находится на расстоянии a от бесконечной проводящей плоскости

Если V полупространство z>0, то функция , где точка есть зеркальное изображение точки в граничной плоскости (металл), позволяет найти потенциал электростатического поля в точке A области V

Причем функция G1 позволяет найти решение, как для точечных зарядов, так и для произвольного распределения p(r’)

Поле в полупространстве z>0, можно интерпретировать, как суперпозицию двух полей – поля, создаваемого исходной системой зарядов, и поля, создаваемого зарядом-изображением

Если V есть область вне сферы |r|>R, где находится заряд q, создающий поле, то функция

, где точка r₂’ есть зеркальное изображение точки r₁’ (заряда q) в граничной плоскости (сфере), позволяет найти потенциал электростатического поля в точке A области V

Причем функция G2 позволяет найти решение, как для точечных зарядов, так и для произвольного распределения p(r’)

Второй член в формуле можно интерпретировать как вклад индуцированного заряда (-q), симметричного данному q, относительно поверхности сферы (металл)

23. Электроемкость уединенного проводника

Рассмотрим заряженный проводник (очевидно, плотность распределения заряда по поверхности проводника, в общем случае, неравномерна)

Пусть проводник находится в однородной изотропной диэлектрической среде с проницаемостью - тогда потенциал (поля) в произвольной точке A поверхности проводника

По определению, поверхность проводника эквипотенциальна – следовательно, выражение для потенциала поверхности не должно зависеть от радиус-вектора r – поэтому введем функцию такую, что тогда величина зависит только от формы проводника и, следовательно, потенциал поверхности проводника , где С-электроемкость уединенного проводника