16. Основная задача электростатики для поля в диэлектрике (истинные и связанные заряды).

О

сновной задачей электростатики называют задачу нахождения электростатического поля (т.е. напряжённости и потенциала) по заданному распределению зарядов.

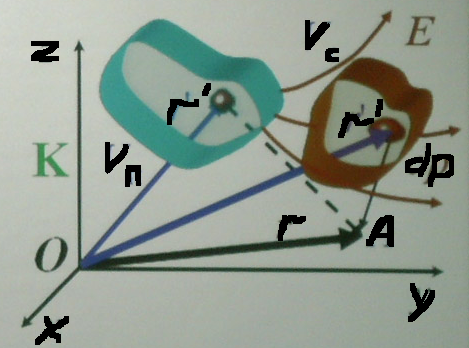
Рассмотрим систему распределённых с

плотностью p(r’) зарядов, занимающих

некоторый объём пространства V_и и

диэлектрик с объёмом V_c.

Потенциал электростатического поля,

создаваемого в точке пространства А

распределёнными зарядами, равен:

Поле, создаваемое зарядами, поляризует

диэлектрик – в результате, каждый

элементарный дипольный момент dp диэлектрика, тоже создаёт электростатическое поле

Индексы и и с, введенные нами, обозначают, соответственно, заряды истинные и связанные(т.е. наведённые в диэлектрике внешним полем – эти заряды не могут свободно двигаться).

Прежде всего, запишем выражение для поля элементарного диполя через вектор поляризации:

Проинтегрируем это выражение по всему пространству:

Первый интеграл преобразуем по теореме Остроградского к интегралу по замкнутой поверхности S, охватывающей объём V:

0

Последний интеграл описывает поток вектора P |r-r’| через замкнутую поверхность, охватывающую всё пространство – т.е. поток за бесконечность, который, по физическим соображениям обязан быть равен нулю.

По объёму диэлектрика Vc, получим поле, создаваемое всем объёмом диэлектрика

Формула описывает потенциал

электростатического поля связанных

зарядов – зарядов, возникающих за

счёт поляризации диэлектрика.

Соответственно, величину

называют

плотностью связанных зарядов.

По принципу суперпозиции результирующее электростатическое поле, создаваемое системой истинных и связанных зарядов, в точке А равно (здесь интегрирование по всему пространству):

Основная задача электростатики для поля в диэлектрике.

17. Уравнение Пуассона для поля в диэлектрике.

Для вакуума мы получили два способа описания электростатического поля:

Основная задача электростатики	Дифференциальные уравнения

где - тогда можно написать дифференциальное уравнение, которое называют уравнением Пуассона для поля в диэлектрике:

- уравнение Пуассона для поля в диэлектрике.

18. Теорема Гаусса для поля в диэлектрике (+вектор электрического смещения).

Электростатическое поле всегда потенциально:

Следовательно, уравнение Пуассона можно записать в виде:

Введём вектор электрического смещения электрического поля:

Таким образом, мы получаем теорему Гаусса в дифференциальной форме для электростатического поля в диэлектрике:

Дивергенция вектора электрического смещения электростатического поля в любой точке пространства пропорциональна плотности истинных зарядов в этой точке.

Вектор электрического смещения электростатического поля называют также вектором индукции электростатического поля.

19. Теорема Гаусса для поля в диэлектрике (интегральная форма).

Д ля того чтобы записать теорему Гаусса в интегральной форме нам понадобится теорема Остроградского:

Поток вектора индукции электростатического поля через замкнутую поверхность, охватывающую произвольное заряженное тело, пропорционален заряду тела.

Вернёмся к вектору электрического смещения электростатического поля: - если диэлектрическая среда однородна и изотропна, то можно написать, где ε – диэлектрическая проницаемость среды(диэлектрика). При помощи формулы, теорему Гаусса (в диф.форме) и

уравнение Пуассона для электростатического поля в диэлектрике можно записать в виде:

где E₀ и φ₀ – напряжённость и потенциал электростатического поля в вакууме.

Электростатическое пол внутри однородного изотропного диэлектрика в ε раз меньше электростатического поля в вакууме.

П

С

оместим однородный

изотропный

диэлектрик во

внешнее

электростатическое

поле с

напряженностью

Е₀ – диэлектрик

поляризуется.

Соответственно,

внутри

диэлектрика возникает электростатическое поле (связанных зарядов)

напряженность Е^с которого, направлена против внешнего электростатического поля (от + к -).

Таким образом, результирующая напряженность электростатического поля в диэлектрике всегда меньше напряженности поля в вакууме:

Рассмотрим теперь два точечных заряда q и q₀, находящихся в однородном изотропном диэлектрике – поля этих зарядов, поляризуют диэлектрик.

Соответственно, сила, действующая на каждый из зарядов:

где F₀ – сила кулоновского

взаимодействия зарядов, а

F – результирующая сила, действующая

со стороны диэлектрика и второго заряда.