
- •1. Закон Кулона. Закон сохранения заряда. Принцип суперпозиции.
- •2. Электростатическое поле (напряженность электростатического поля, поле точечного покоящегося электрического заряда, потенциальность поля)
- •3. Основная задача электростатики (для точечных зарядов в вакууме, для произвольного объемного, поверхностного и линейного распределения зарядов)
- •4. Дифференциальные операторы (оператора (набла), дивергенция функции divF, ротор функции rotF)
- •5. Безвихревой характер электростатического поля
- •6. Поток вектора напряженности
- •7. Теорема Гаусса (в том числе - для точечного заряда)
- •8. Применение теоремы Гаусса для расчета полей - поле бесконечной, прямой, равномерно заряженной нити
- •9. Применение теоремы Гаусса для расчета полей - поле бесконечной, равномерно заряженной плоскости
- •10. Применение теоремы Гаусса для расчета полей - поле сферической, равномерно заряженной поверхности
- •11. Теорема Гаусса в дифференциальной форме (вакуум).
- •12. Уравнение Пуассона (вакуум).
- •13. Плотность заряда для точечного заряда (δ-функция).
- •14. Поле Диполя.
- •15. Диэлектрики и вектор поляризации.
- •16. Основная задача электростатики для поля в диэлектрике (истинные и связанные заряды).
- •17. Уравнение Пуассона для поля в диэлектрике.
- •19. Теорема Гаусса для поля в диэлектрике (интегральная форма).
- •20. Закон Кулона в диэлектрике (Теорема Гаусса для поля в диэлектрике).
- •21. Свойства проводников
- •22. Метод изображений (для бесконечно проводящей плоскости и сферы)
- •23. Электроемкость уединенного проводника
- •24. Конденсатор – Сферический конденсатор
- •25. Конденсатор – Плоский конденсатор
- •26. Конденсатор – Соединения конденсаторов
- •27. Энергия заряженного проводника
- •28. Энергия электростатического поля
- •29. Ток и плотность тока
- •1. Работа тока (вдоль произвольного контура, мощность и удельная мощность тока)
- •2. Интегральные закона Ома (для участка цепи, содержащего эдс - определение эдс и сопротивления участка цепи; для замкнутого проводника; для участка цепи не содержащего эдс)
- •3. Закон Ома в дифференциальной форме.
- •4. Тепловое действие тока (закон Джоуля-Ленца в дифференциальной и интегральной формах)
- •5. Правила Кирхгофа.
- •6 . Постулат Ампера
- •7. Закон Био-Савара-Лапласса
- •8. Силовое действие магнитного поля – закон Ампера
- •9. Закон Ампера: сила Лоренца, сила Ампера
- •10. Силовое действие магнитного поля – принцип действия электромотора
- •11. Силовое действие магнитного поля – принцип действия электромотора.
- •12. Калибровочная инвариантность магнитного поля
- •13. Применение закона бсл для расчета магнитных полей – поле бесконечного, прямого проводника с постоянным током.
- •14. Применение закона бсл для расчета магнитных полей – поле кругового проводника с постоянным током.
- •15. Закон полного тока – уравнение Пуассона для магнитного поля.
- •16. Закон полного тока (в дифференциальной и интегральной формах)
- •17. Применение закона полного тока для расчета магнитных полей – поле бесконечного, прямого проводника с постоянным током.
- •18. Применение закона полного тока для расчета магнитных полей – поле бесконечного соленоида с постоянным током.
- •19. Теорема Гаусса для магнитного поля.
- •20. Магнитный момент.
- •21. Магнитная восприимчивость
- •22. Закон полного тока для магнитного поля в магнетике
- •23. Уравнение Пуассона для магнитного поля в магнетике
- •24. Векторный потенциал магнитного поля в магнитной среде
- •25. Типы магнетизма (Суперпарамагнетизм, Антиферромагнетизм (Клапаны вращения), Ферримагнетизм, Ферромагнетизм (Ферромагнитные материалы), Парамагнетизм, Диамагнетизм)
- •26. Магнетизм вещества.
4. Дифференциальные операторы (оператора (набла), дивергенция функции divF, ротор функции rotF)
В
механике было определение оператора
(набла):
![]() ,
его действие на скалярную
функцию называют градиентом
этой функции
,
его действие на скалярную
функцию называют градиентом
этой функции
![]() .
.
Очевидно, что оператор-вектора (набла) можно умножать не только на скалярные функции, но и на векторные(например, напряжённость электростатического поля E(r)) – так как для векторов существует два типа произведений, то возникает две дополнительные дифференциальные операции с оператором .
Скалярное произведение оператора на векторную функцию F(r) называют дивергенцией этой функции divF(r)
![]() .
.
Векторное произведение оператора на векторную функцию F(r) называют ротором этой функции rotF(r)
![]()
5. Безвихревой характер электростатического поля
В екторное
поле F,
ротор которого не равен нулю rotF
екторное
поле F,
ротор которого не равен нулю rotF![]() 0,
называют вихревым полем – такое поле
не имеет источников и его силовые линии
замкнуты сами на себя.
0,
называют вихревым полем – такое поле
не имеет источников и его силовые линии
замкнуты сами на себя.
П роверим,
является ли электростатическое поле
вихревым – вычислим ротор напряжённости
такого поля
роверим,
является ли электростатическое поле
вихревым – вычислим ротор напряжённости
такого поля
![]()
0
Следовательно:
Электростатическое поле безвихревое – ротор напряжённости такого поля равен нулю
Это означает:
Силовые линии электростатического поля никогда не замыкаются сами на себя, они начинаются или заканчиваются на заряде
6. Поток вектора напряженности
Р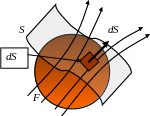 ассмотрим
некоторую гладкую
поверхность S
– к любой точке такой поверхности, можно
построить касательную
сферу
ассмотрим
некоторую гладкую
поверхность S
– к любой точке такой поверхности, можно
построить касательную
сферу
Тогда, элементарный вектор dS, проведённый из точки касания(от центра касательной окружности) и равный по величине площади элементарной поверхности dS в окрестности точки касания называют вектором нормали к поверхности.
Если,
при этом, в пространстве есть векторное
поле F,
то скалярное произведение FdS
называют элементарным
потоком
вектора F
![]() .
.
Интегрируя
по всей поверхности S,
получим поток
![]() вектора
F
через поверхность S
вектора
F
через поверхность S
![]()
Соответственно,
для электростатического поля с
напряжённостью E,
величину
![]() ,
называют потоком вектора напряжённости
через поверхность S
,
называют потоком вектора напряжённости
через поверхность S
7. Теорема Гаусса (в том числе - для точечного заряда)
Р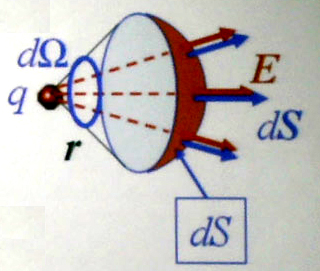 ассмотрим
точечный заряд q
– элементарный поток вектора напряжённости
электростатического поля E
через элементарную поверхность dS
равен
ассмотрим
точечный заряд q
– элементарный поток вектора напряжённости
электростатического поля E
через элементарную поверхность dS
равен
![]()
По
определению скалярного произведения
![]() (где
(где
![]() -
проекция вектора dS
на радиус-вектор r).
-
проекция вектора dS
на радиус-вектор r).
Элементарный
объёмный угол под которым видна площадка
dS
называют элементарным телесным углом
![]() .
.
![]()
Таким
образом получаем теорему Гаусса для
точечного заряда
![]()
Элементарный
поток
![]() вектора напряжённости электростатического
поля E
точечного заряда q
в заданный телесный угол
зависит только от величины заряда q.
вектора напряжённости электростатического
поля E
точечного заряда q
в заданный телесный угол
зависит только от величины заряда q.
Р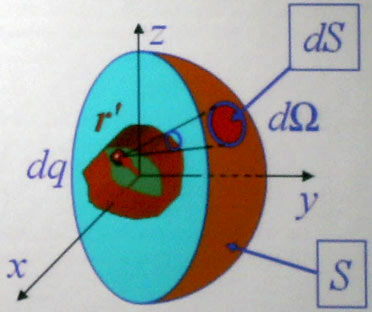 ассмотрим
заряженное тело – для любого элементарного
заряда dq
внутри этого тела выполняется теорема
Гаусса
причём
ассмотрим
заряженное тело – для любого элементарного
заряда dq
внутри этого тела выполняется теорема
Гаусса
причём
![]()
Окружим
заряженное тело замкнутой поверхностью
S(не
обязательно сферой), но так, чтобы dS
лежала на S.
Тогда элементарный поток
![]() для
элементарного заряда dq
через всю замкнутую поверхность S
будет равен
для
элементарного заряда dq
через всю замкнутую поверхность S
будет равен
![]()
Очевидно
каждый элементарный объём
![]() заряженного
тела(имеющий заряд dq)
создаёт одинаковый поток
заряженного
тела(имеющий заряд dq)
создаёт одинаковый поток
![]() через
замкнутую поверхность S.
через
замкнутую поверхность S.
Интегрируя
по всему объёму тела, получим Теорему
Гаусса:![]()
Поток вектора напряжённости электростатического поля через замкнутую поверхность, охватывающую произвольное заряженное тело, пропорционален заряду тела.
