
- •Предисловие
- •Глава 1. Квантовая случайность. Анализ взаимно- дополнительных статистических величин.
- •1.1. Статистическая интерпретация прямого и обратного преобразований Фурье. Координатное и импульсное распределения.
- •1.2. Принцип дополнительности н. Бора
- •1.3. Характеристическая функция. Вычисление среднего и моментов. Неполнота классической и полнота квантовой статистики.
- •1.4. Операторы координаты и импульса в координатном и импульсном представлении. Фундаментальные коммутационные соотношения
- •Глава 2. Точность статистических характеристик гильбертова пространства
- •2.1. Неравенство Коши- Буняковского для векторов состояния и его статистическая интерпретация
- •2.2.Неравенство Коши- Буняковского в приложении к случайным величинам
- •2.3. Соотношение неопределенностей Гейзенберга для координаты и импульса
- •2.4. Соотношение неопределенностей Шредингера- Робертсона
- •2.5. Многомерное соотношение неопределенностей
- •2.6. Информация Фишера
- •2.7. Неравенство Рао- Крамера
- •2.8. Многомерное неравенство Рао- Крамера и корневая оценка
- •Глава 3. Принципы квантовой информатики и шестая проблема Гильберта
- •3.1 Постулаты квантовой информатики
- •3.2 От квантовой информатики к квантовой физике
- •3.3. Шестая проблема Гильберта
- •3.4 Обсуждение
- •3.П. Приложение. Разложение Шмидта и формализм матрицы плотности.
- •Основная числовая характеристика, связанная с разложением Шмидта есть число Шмидта , которое характеризует эффективное число мод в разложении:
- •Глава 4. Основные логические элементы квантовой информатики и их свойства
- •4.2. Реализация произвольного состояния кубита посредством унитарного поворота.
- •4.3. Система кубитов
- •4.4. Измерение кубитов
- •4.5. Простейшие квантовые логические элементы
- •4.6. Преобразование Уолша-Адамара (Walsh-Hadamar Transformation)
- •4.8. Состояния Белла
- •Состояния Белла относят к классу так называемых эпр состояний. Такой термин возник в связи с парадоксом (эффектом) Эйнштейна - Подольского – Розена, который рассматривается ниже.
- •4.9 Парадокс (эффект) Эйнштейна - Подольского - Розена
- •4.10 Неравенство Белла
- •4.11. Физическая реализация кубита. Спиновой магнитный резонанс.
- •Глава 5. Некоторые алгоритмы квантовой информатики
- •5.1. Сверхплотное кодирование.
- •5.2. Телепортация
- •5.3. Квантовый параллелизм. Алгоритмы Дойча и Дойча- Джозсы.
- •5.4. Квантовое преобразование Фурье.
- •5.5. Нахождение периода функции
- •5.6 Факторизация чисел
- •5.7. Квантовая криптография
- •5.8. Алгоритм Гровера
- •5.9 Введение в квантовое исправление ошибок
2.6. Информация Фишера
Рассмотрим квантовую
систему, для которой пси- функция
действительна:
![]() .
Использование таких пси- функций
представляет собой простейший способ
дополнения классической плотности
распределения до квантового состояния.
Для такой системы средний импульс равен
нулю, а квадрат импульса есть:
.
Использование таких пси- функций
представляет собой простейший способ
дополнения классической плотности
распределения до квантового состояния.
Для такой системы средний импульс равен
нулю, а квадрат импульса есть:
![]()
Здесь штрих означает производную по .
Введем информацию Фишера, связанную с дисперсией импульса:
![]()
Тогда соотношение неопределенностей запишется в виде следующего неравенства:
![]()
Полученное неравенство аналогично неравенству Рао- Крамера, рассматриваемому в следующем разделе
2.7. Неравенство Рао- Крамера
Рассмотрим снова
ситуацию, когда плотность распределения
дополняется до квантового состояния.
Пусть распределение вероятностей и
соответствующее квантовое состояние
зависят от некоторого действительного
параметра
![]() ,
т.е.:
,
т.е.:
![]() .
.
Пусть
![]() есть несмещенная оценка неизвестного
параметра
,
основанная на выборке объема
есть несмещенная оценка неизвестного
параметра
,
основанная на выборке объема
![]() в координатном пространстве, т.е.
в координатном пространстве, т.е.
![]() .
.
Условие несмещенности означает, что среднее значение (математическое ожидание) выборочной оценки совпадает с истинным значением параметра , т.е.
![]()
Примерами несмещенных оценок могут служить известные оценки математического ожидания и дисперсии [31]:
![]()
![]()
Пусть
![]() - оператор, канонически сопряженный
параметру
- оператор, канонически сопряженный
параметру
![]() .
.
Нашей целью является вывод следующего соотношения, называемого неравенством Рао-Крамера:
![]()
Здесь введена информация Фишера, которая имеет вид:
![]()
Воспользуемся тем, что вектор состояния для выборки может быть определен следующим выражением
![]()
Проведем подробные
вычисления. Пусть
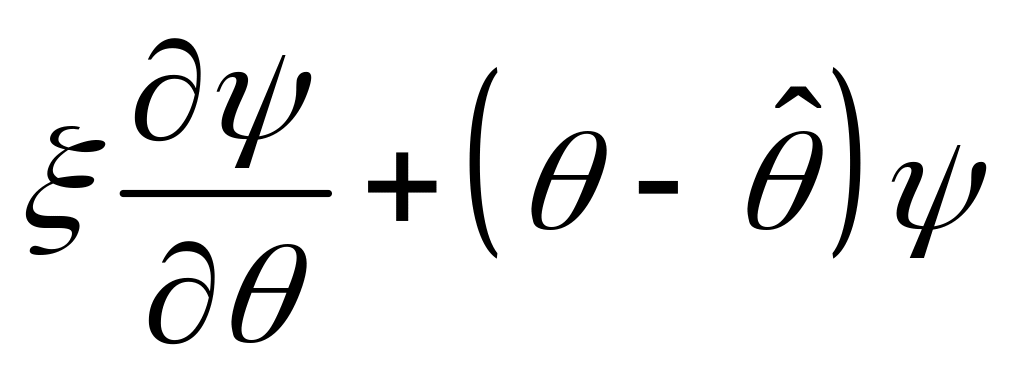 -
кет вектор, где
-
кет вектор, где![]() ,
как и ранее, произвольный действительный
параметр,
,
как и ранее, произвольный действительный
параметр,
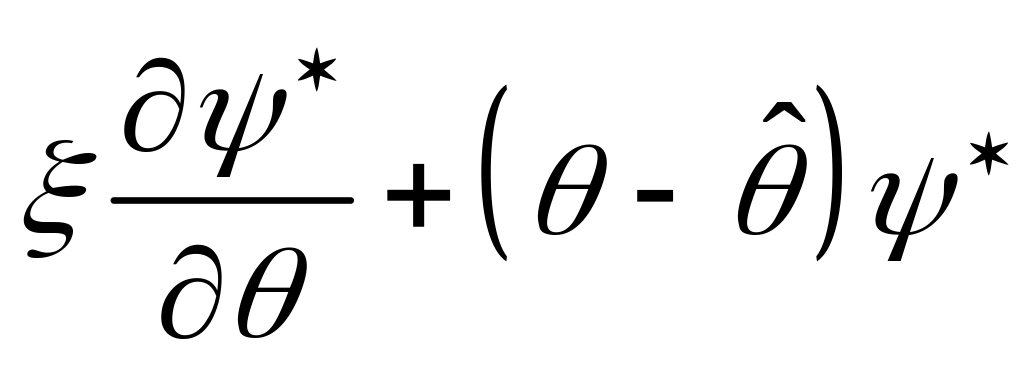 -
соответствующий бра- вектор.
-
соответствующий бра- вектор.
Заведомо неотрицательное выражение есть:
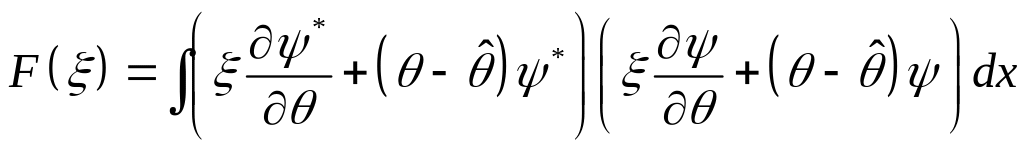
Здесь для сокращения
записи мы полагаем, что
![]() ,
,
![]()
В развернутой записи имеем:
![]() ,
,
где
![]()
![]()
![]()
Можно показать,
что
![]() .
Для этого достаточно представить
подинтегральное выражение с помощью
формулы для производной произведения
в виде
.
Для этого достаточно представить
подинтегральное выражение с помощью
формулы для производной произведения
в виде
![]()
Интеграл от первого слагаемого равен нулю в силу несмещенности оценки. В результате, учитывая условие нормировки, получаем, что .
Из условия
![]() для дискриминанта получаем искомый
результат – неравенство Рао-Крамера
[38- 40]:
для дискриминанта получаем искомый
результат – неравенство Рао-Крамера
[38- 40]:
![]()
Заметим, что мы провели вычисления не только для предполагаемого случая действительных векторов состояния, но и для более общего случая комплексных пси- функций.
В этом случае информация Фишера есть:
![]()
Информация Фишера является аналогом дисперсии импульса и отличается от последней множителем 4 и тем, что под интегралом идет дифференцирование по параметру, а не по координате.
Для случая действительных пси- функций, как нетрудно показать, имеет место приведенное выше выражение для информации Фишера (6). При выводе следует воспользоваться легко проверяемым свойством аддитивности информации Фишера (информация от независимых представителей в раз превосходит информацию от одного представителя).
Полученное
неравенство, очевидно, является наиболее
сильным для случая, когда информация
Фишера
![]() минимальна. Как и в случае соотношения
неопределенности Гейзенберга, можно
показать, что добавление произвольного
фазового множителя к действительной
пси- функции не может привести к уменьшению
информации Фишера.
минимальна. Как и в случае соотношения
неопределенности Гейзенберга, можно
показать, что добавление произвольного
фазового множителя к действительной
пси- функции не может привести к уменьшению
информации Фишера.
Выше мы видели, что соотношение неопределенностей из неравенства превращается в равенство для гауссова состояния. Аналогичный результат справедлив и для неравенства Рао- Крамера. Последнее превращается в равенство для оценок, имеющих нормальное распределение и только для них. Такие оценки называются эффективными.
Выше мы предполагали несмещенность статистической оценки. Однако, проведенные выкладки позволяют также получить более общее неравенство Рао- Крамера, пригодное и для смещенных оценок. В этом случае оно имеет вид:
![]() (2.1)
(2.1)
где
![]() - смещение оценки. (2.2)
- смещение оценки. (2.2)
Заметим, что в представленном неравенстве слева вместо обычной дисперсии стоит величина, которая характеризует рассеяние выборочной оценки относительно истинного значения .
Задача 2.1 Обоснуйте неравенство Рао- Крамера (2.1)- (1.2), учитывающее возможную смещенность оценки.
