2.2.Неравенство Коши- Буняковского в приложении к случайным величинам

Пусть и - действительные случайные величины, представляющие собой произвольные функции от координаты . Пусть - действительный параметр. Рассмотрим заведомо неотрицательную функцию от :

В развернутой записи рассматриваемая функция представляет собой квадратный трехчлен:

Условие неотрицательности означает, что дискриминант меньше или равен нулю:

Таким образом для любых (коммутирующих) случайных величин выполняется неравенство Коши- Буняковского:

В частности, если в качестве случайных величин рассмотреть величины и , приведенные к нулевым средним значениям, то для дисперсий получим неравенство:

.

Из последнего выражения следует неравенство для коэффициента корреляции

Напомним, что коэффициент корреляции между случайными величинами и определяется формулой:

Квадрат коэффициента корреляции иногда называют коэффициентом детерминации. Этот коэффициент показывает, в какой мере случайная величина определяет (детерминирует) случайную величину и наоборот.

Можно показать, что неравенство Коши- Буняковского обращается в равенство в том и только том случае, когда случайные величины и линейно связаны между собой.

2.3. Соотношение неопределенностей Гейзенберга для координаты и импульса

Модифицируем приведенный выше пример. Рассмотрим вместо выражение . Заметим, что оператор производной не является эрмитовым, потому что . Чтобы запись сделать более наглядной введем эрмитов оператор импульса .

Рассмотрим как и при выводе неравенства Коши- Буняковского заведомо неотрицательную функцию от действительного параметра

В развернутой записи имеем:

Учтем каноническое коммутационное соотношение

В качестве наблюдаемых рассмотрим величины и , которые, очевидно, удовлетворяют тому же коммутационному соотношению. Тогда для произведения дисперсий координаты и импульса получим искомое соотношение неопределенностей Гейзенберга :

Дисперсия импульса есть средний квадрат импульса минус средний импульс в квадрате:

В развернутой записи средний квадрат импульса есть:

Как следует из приведенных выкладок, неравенство обращается в равенство в том и только том случае, когда при некотором :

Это равенство имеет место только для гауссова состояния (основного состояния гармонического осциллятора).

Решение полученного уравнения в координатном и импульсном представлении соответственно есть:

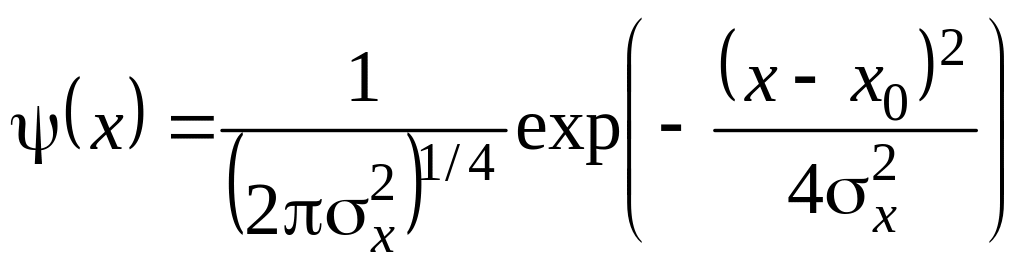
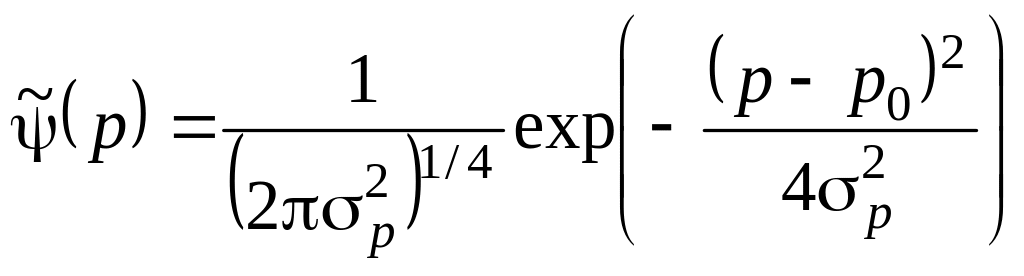
Здесь и - соответственно среднее и дисперсия для распределения координаты, а и - соответственно среднее и дисперсия для распределения импульса.

Дисперсия координаты и импульса полученного гауссовского состояния определяются введенным параметром

,

Таким образом, рассматриваемые величины оказываются связанными между собой минимальным соотношением неопределенностей:

Мы видим, что состояние, минимизирующее соотношение неопределенностей, описывается действительной функцией. Это обстоятельство неслучайно. Нетрудно видеть, что добавление произвольного фазового множителя к действительной координатной пси- функции не может уменьшить дисперсию импульса и, таким образом, не может усилить рассматриваемое неравенство.