
- •2. Классификация и способы представления систем
- •2.1. Произвольно-схематический и схематически-символический
- •2.2. Описание систем на языке математических символов
- •2.3. Графическое изображение систем
- •2.4. Представление систем с помощью матриц
- •2.5. Представление систем в форме семантических сетей
- •2.6. Классификация систем
2. Классификация и способы представления систем
В зависимости от целей исследования, природы, сложности и масштабов систем, а также ряда других факторов могут быть использованы различные способы их представления и изображения. Рассмотрим несколько наиболее распространённых способов представления и изображения систем.
2.1. Произвольно-схематический и схематически-символический
способы представления систем
Примером произвольно-схематического представления системы является следующее изображение:
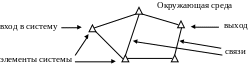
Схематически–символическое представление (изображение) некой системы выглядит следующим образом:

СИСТЕМА
При схематически-символическом изображении систем используют следующие основные термины:
Входы – элементы внешней среды, которые система преобразует в выходы. Совокупность всех входов составляет обобщенный вход.
Выход – это результат работы системы. Совокупность всех выходов может быть сведена к обобщенному выходу.
Обратная связь – информация (сигнал), поступающий с выхода системы на её вход. Обратная связь может быть положительной, если сигнал подаётся в той же фазе, или отрицательной, если сигнал поступает в противофазе.
Процессор – механизм, преобразующий входные элементы в выходные.
Параметр – величина, характеризующая некоторое существенное свойство процесса или явления.
Свойства – выходы управляемой системы, характеризующие её состояние на заключительном или промежуточном этапе.
Алгоритм процесса – последовательность определённых операций, позволяющая определять или реализовывать цели системы при соблюдении накладываемых ограничений.
С
 истему
типа «процесс» принято изображать
прямоугольником (как на рисунке). Систему
типа «объект» изображают овалом ( ).
Систему типа «процесс принятия решения»
изображают ромбом ( ).
истему
типа «процесс» принято изображать
прямоугольником (как на рисунке). Систему
типа «объект» изображают овалом ( ).
Систему типа «процесс принятия решения»
изображают ромбом ( ).
2.2. Описание систем на языке математических символов
Систему можно представить и с помощью широко используемого в математике понятия «множество». В общем случае, множество это совокупность каких либо реально наблюдаемых или мыслимых (т.е. абстрактных) объектов. Абстрактные математические множества по количеству и виду элементов бывают конечными и бесконечными, упорядоченными и неупорядоченными. (Например, множество натуральных чисел или множество решений некоторого уравнения).
Если некая система представлена как множество Х, то принадлежность элемента а к этому множеству отражают следующим образом: а Х. Если элемент а не принадлежит множеству Х, то пишут: а Х. Если любой элемент множества Х является также элементом множества У, то тогда множество Х называют подмножеством множества У и отражают это с помощью следующей записи: Х У. Если Х У и Х У, то тогда множество Х тождественно множеству У (Х = У).
Конечное, упорядоченное множество М, состоящее из n элементов типа а, описывают следующим образом: М = {а1, а2 ,…аi ,…аn}. Пустое множество, не содержащее ни одного элемента, изображают символом .
В математических записях знак означает объединение. Объединением множеств Х и У (Х У) является такое множество, каждый элемент которого принадлежит либо множеству Х, либо множеству У.
Знак означает пересечение. Пересечением множеств Х и У (Х У) является такое множество, каждый элемент которого принадлежит одновременно и множеству Х, и множеству У.
Знак \ означает разность. Разностью множеств Х и У (Х \ У) является такое множество, каждый элемент которого принадлежит множеству Х, но не принадлежит множеству У.
Символ | ставится вместо слов «такие, что», «такой, что». Знак означает «существует хотя бы одно (один)»,а знак – «для всех». Символ означает логическую операцию «или», а символ – логическую операцию «и».
Примером описания систем на языке математических символов являются следующие записи: АВ = х (хА) (хВ); или х (х) = min.
