Циклические коды

Циклические коды позволяют обнаруживать и исправлять ошибки при передаче бинарных кодов через канал с помехами.

Идея построения циклических кодов базируется на использовании неприводимых в поле двоичных чисел многочленов. Неприводимые многочлены (как и простые числа) делятся без остатка только на себя или на единицу.

Идея коррекции ошибок в циклических кодах базируется на том, что разрешенные комбинации кода – В(Х) – делятся без остатка на некоторый образующий (порождающий, производящий, генераторный) многочлен – К(Х), который выбирается из числа неприводимых многочленов. Для обнаружения ошибки при делении на выбранный многочлен надо, чтобы все комбинации кода не делились ни на какой другой многочлен, т.е. чтобы выбранный многочлен – К(Х) – не разлагался на другие многочлены, т.е. был простым неприводимым многочленом.

Очевидно, что в качестве многочлена В(Х) можно использовать произведение:

В(Х) = И(Х) * К(Х),

где: И(Х) – информационный многочлен (исходный передаваемый код).

Но при этом информационные и проверочные символы (биты) оказываются перемешанными, что затрудняет процесс декодирования.

Поэтому на практике применяют другой метод для нахождения циклического кода В(Х). Обозначим разрядность циклического кода – n; количество информационных символов (битов) – i; разрядность избыточных (проверочных) битов – k. При этом: n = i + k.

Умножим многочлен И(Х) на Х^k и полученное произведение разделим на образующий многочлен К(Х):

И(Х) * Х^k = М(Х) * К(Х) С(Х),

где: М(Х) – частное;

С(Х) – остаток.

Т.к. операции суммирования и вычитания «по модулю два» совпадают, то это выражение перепишем в форме:

И(Х) * Х^k С(Х) = М(Х) * К(Х).

Из этого уравнения следует, что многочлен И(Х) * Х^k С(Х) делится без остатка на образующий многочлен К(Х), поэтому его можно использовать как циклический код В(Х).

Многочлен И(Х) * Х^k имеет разрядность n, а также следующую структуру: младшие k битов равны нулю, а старшие i символов совпадают с информационным многочленом И(Х). Процесс кодирования заключается в нахождении остатка С(Х) от деления И(Х) * Х^k на образующий многочлен К(Х) с последующим сложением «по модулю 2» найденного остатка с многочленом И(Х) * Х^k .

Для примера рассмотрим кодирование четырехбитового числа 10₍₁₀₎ = 1010₍₂₎. Для i = 4 рассчитываем количество проверочных битов k = 3 . По таблице неприводимых многочленов [Цымбал В.П. Теория информации и кодирование.– К.: Выща шк., 1992] находим многочлен со степенью k = 3 : К(Х) = 1101.

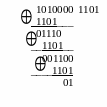
О статок от деления: 001 добавляем на место проверочных битов. Поэтому сформированный циклический код имеет вид: В(Х) = 1010001.

Э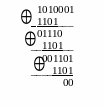 тот код без остатка делится на образующий многочлен К(Х) = 1101.

Если на приемной стороне циклический код В’(Х) делится без остатка на образующий многочлен К(Х), то сигнал принят без искажений.

Ошибки в циклических кодах обнаруживаются и исправляются при помощи остатков от деления принятой кодовой комбинации В’(Х) на образующий многочлен. Остатки от деления являются опознавателями ошибок, но не указывают непосредственно на место ошибки в принятом циклическом коде.

Обнаружение и исправление ошибок в циклических кодах происходит по остаткам от деления принятой комбинации В’(Х) на образующий многочлен К(Х). Если принятая комбинация делится на образующий многочлен без остатка, то код принят безошибочно.

Остаток от деления свидетельствует об ошибке. Чтобы определить ошибочный разряд и исправить его, выполняют следующие процедуры:

1. Принятая комбинация В’(Х) делится на образующий многочлен К(Х).

2. Подсчитывается количество единиц в остатке (вес остатка – W). Если вес остатка – W ≤ S, где S – допустимое число исправляемых данным кодом ошибок, то принятая комбинация складывается «по модулю 2» с полученным остатком. Сумма даст исправленную комбинацию. Если в остатке W > S, то

3. Принятая комбинация В’(Х) циклически сдвигается на один разряд влево (или вправо) и

4. Делится на образующий многочлен К(Х). Если в остатке W ≤ S, то складывается сдвинутая комбинация с остатком. Затем производится обратный циклический сдвиг вправо (или влево) для компенсации предыдущего сдвига влево (или вправо) и восстановления принятой комбинации уже без ошибок. Если в этом остатке W > S, то повторяется процедура 3 и 4 до тех пор, пока не будет W ≤ S. В этом случае комбинация, полученная в результате последнего циклического сдвига (делимое), суммируется с остатком и производится обратный циклический сдвиг вправо (или влево) до восстановления принятой комбинации уже без ошибок.

Для числа 10₍₁₀₎ правильный циклический код с образующим многочленом К(Х) = 1101 имеет вид В(Х) = 1010001.

Допустим, на приемной стороне искаженная комбинация имеет вид: В’(Х) = 1011001, т.е. четвертый справа символ изменился с «0» на «1».

Делим принятую комбинацию на образующий многочлен:

С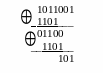 равниваем вес полученного остатка W = 2 с возможным для данного кода числом исправляемых ошибок S = 1.

Производим циклический сдвиг принятой комбинации В’(Х) влево на один разряд с последующим делением на образующий многочлен К(Х):

С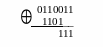 равниваем вес полученного остатка W = 3 с возможным для данного кода числом исправляемых ошибок S = 1.

П роизводим еще один циклический сдвиг влево на один разряд с последующим делением на образующий многочлен К(Х). Повторяем эти сдвиги и деления до тех пор, пока W = S:

Складываем «по модулю 2» последнее делимое с последним остатком:

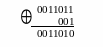
Производим циклический сдвиг полученной комбинации на 4 разряда вправо (или 3 разряда влево) до восстановления исходного положения принятого кода, но уже без ошибок: 1010001.