
Федеральное агентство по образованию Российской Федерации
Санкт-Петербургский государственный горный институт им. Г.В. Плеханова
(технический университет)

Отчёт по лабораторной работе № 11 По дисциплине: Физика
(наименование учебной дисциплины согласно учебному плану)
Тема: Исследование процессов накопления и релаксации заряда в диэлектрических материалах
Выполнил: студент ______________ /
(подпись) (Ф.И.О.)
ОЦЕНКА: _____________
Дата: __________________
Проверил: ассистент ____________ /./
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
2011 год
Цель работы: 1. Определение постоянной времени RC-цепи. 2. Определение входного сопротивления вольтметра путем измерения разрядных характеристик конденсатора. 3. Оценка величины заряда, не связанного с поляризацией диэлектрика в конденсаторе.
Теоретические основы лабораторной работы
В цепях постоянного тока распределение электрических зарядов на проводниках и токов на участках цепи стационарно, то есть неизменно во времени. Электромагнитное поле в таких цепях состоит из электростатического поля неподвижных зарядов и магнитного поля постоянных токов. Эти поля существуют независимо друг от друга.
Если на каком-то
участке цепи происходят изменения силы
тока или напряжения, то другие участки
цепи могут «почувствовать» эти изменения
только через некоторое время, которое
по порядку величины равно времени τ
распространения электромагнитного
возмущения от одной точки цепи к другой.
Так как электромагнитные возмущения
распространяются с конечной скоростью,
равной скорости
света c,
то
![]() ,
где l
– расстояние между наиболее удаленными
точками цепи. Если это время τ
много меньше длительности процессов,
происходящих в цепи, то можно считать,
что в каждый момент времени сила тока
одинакова во всех последовательно
соединенных участках цепи. Процессы
такого рода в электрических цепях
называются квазистационарными.
,
где l
– расстояние между наиболее удаленными
точками цепи. Если это время τ
много меньше длительности процессов,
происходящих в цепи, то можно считать,
что в каждый момент времени сила тока
одинакова во всех последовательно
соединенных участках цепи. Процессы
такого рода в электрических цепях
называются квазистационарными.
Квазистационарные процессы можно исследовать с помощью законов постоянного тока, если применять эти законы к мгновенным значениям сил токов и напряжений на участках цепи.
Из-за огромного значения скорости света время установления электрического равновесия в цепи оказывается весьма малым. Поэтому к квазистационарным можно отнести многие достаточно быстрые в обычном смысле процессы. Например, быстрые колебания в радиотехнических цепях с частотами порядка миллиона колебаний в секунду и даже выше очень часто еще можно рассматривать как квазистационарные.
П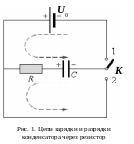 роцессы,
протекающие во времени в цепях обычно
являются медленными в рассматриваемом
смысле. В данной работе рассматривается
процесс накопления заряда на конденсаторе
С
(т.е. его зарядка от источника напряжения)
и релаксация этого заряда (т.е. разряд
конденсатора) в цепи сопротивлением R.
Ниже будет показано, что при разумных
значениях емкости и сопротивления
данный процесс можно считать
квазистационарным.
роцессы,
протекающие во времени в цепях обычно
являются медленными в рассматриваемом
смысле. В данной работе рассматривается
процесс накопления заряда на конденсаторе
С
(т.е. его зарядка от источника напряжения)
и релаксация этого заряда (т.е. разряд
конденсатора) в цепи сопротивлением R.
Ниже будет показано, что при разумных
значениях емкости и сопротивления
данный процесс можно считать
квазистационарным.
Рассмотрим процессы зарядки и разрядки конденсатора. Пусть конденсатор емкостью С включен в схему, показанную на рис. 1. Тогда, установив переключатель К в положение 1, мы будем заряжать конденсатор, а в положении 2 – разряжать конденсатор.
Рассмотрим вначале процесс заряда. Обозначим U0 – э.д.с. источника питания, R – сопротивление цепи (внутренним сопротивлением источника пренебрегаем, либо включаем его в значение R), и выберем положительное направление тока как показано на рис. 1. Применяя к зарядному контуру второе правило Кирхгофа, получим
![]() ,
(1)
,
(1)
где I – мгновенное значение силы тока в цепи, Uc – мгновенное значение напряжения на конденсаторе. Но
![]() , (2)
, (2)
![]() , (3)
, (3)
где q – заряд конденсатора, t – время, прошедшее с момента начала заряда, т.е. с момента включения ключа. По физической природе ток через конденсатор является током смещения, связанным с изменением во времени его заряда и напряженности электрического поля в нем. Такой же по величине ток течет и через резистор, но его природа другая – это ток проводимости.
Из (1) – (3) получается дифференциальное уравнение с постоянными коэффициентами для нахождения Uc
![]() . (4)
. (4)
В этом уравнении переменные можно разделить, и в результате интегрирования уравнения с учетом начального условия
при t = 0 Uc = 0 (5)
находим:
![]() (6)
(6)
При t = 0 это выражение дает Uc = 0 в соответствии с начальным условием. При увеличении времени напряжение на конденсаторе непрерывно увеличивается и асимптотически приближается к э.д.с. U0 источника.
Зависимость зарядного тока от времени в соответствии с законом Ома имеет вид:
![]() .
(7)
.
(7)
Таким образом, зарядный ток максимален в начальный момент времени и асимптотически стремится к нулю в процессе зарядки.
В случае разряда конденсатора исходные уравнения будут иметь вид
![]() , (8)
, (8)
![]() , (9)
, (9)
![]() .
(10)
.
(10)
В отличие от предыдущего, в выражение для тока (10) входит знак минус, т.к. выбранное нами положительное направление тока соответствует уменьшению заряда конденсатора.
Исключая из (8) – (10) q и I, получим дифференциальное уравнение
![]() .
(12)
.
(12)
Если непосредственно перед разрядом на конденсаторе было начальное напряжение Uнач, то, с учетом начального условия
при t = 0 Uc = Uнач (13)
интегрированием уравнения (12) получим зависимость напряжения на конденсаторе от времени в процессе его разряда:
![]() .
(14)
.
(14)
Разрядный ток в соответствии с законом Ома при этом
![]() . (15)
. (15)
Таким образом, разрядный ток максимален в начальный момент времени и асимптотически стремится к нулю в процессе разрядки.
Качественно процесс зарядки и разрядки конденсатора во времени показан на рис. 2.
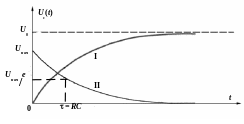
Рис. 2. Зарядка (I) конденсатора от источника э.д.с. и его разрядка (II) через резистор.
Полученные результаты показывают, что процессы накопления заряда в диэлектрике (заряд конденсатора) и релаксации заряда (разряд конденсатора) происходят не мгновенно, а с конечной быстротой. В рассмотренном случае RC – цепи быстрота этих процессов зависит, как видно из (6) и (14), от произведения
![]() ,
(16)
,
(16)
которое имеет
размерность времени и называется
постоянной
времени
RC – цепи.
Как видно из (14), постоянная времени
показывает, через какое время после
начала разряда напряжение на конденсаторе
уменьшается в е = 2,72 раз.
Принято считать в соответствии с (6) и
(14), что процесс заряда и разряда емкости,
практически, полностью заканчивается
за время
![]() .
.
Поскольку реально
используемые емкости могут иметь
небольшой номинал, например,
С = 100 пФ = 10-10 Ф,
на основе разрядной характеристики
возможно измерение больших сопротивлений
и измерение малых токов утечки (с помощью
доступных приборов это не всегда можно
сделать): измеряя процесс разрядки
известной емкости через неизвестное
высокоомное сопротивление и определяя
постоянную времени, легко рассчитать
это сопротивление. Действительно, из
(16) видно, что при
![]() = 100 с
и С = 100 пФ
будем иметь R = 1012 Ом.
Столь большое сопротивление измерить,
например, обычным омметром невозможно,
а измерение интервала времени 100 с
не представляет труда и может быть
осуществлено с большой точностью. Для
того чтобы исключить необходимость
измерения начального напряжения на
конденсаторе при реализации рассматриваемого
способа, измерения производят по
следующей методике. На основе (14) при
разрядке известной емкости С
через определяемое сопротивление R,
можно записать
= 100 с
и С = 100 пФ
будем иметь R = 1012 Ом.
Столь большое сопротивление измерить,
например, обычным омметром невозможно,
а измерение интервала времени 100 с
не представляет труда и может быть
осуществлено с большой точностью. Для
того чтобы исключить необходимость
измерения начального напряжения на
конденсаторе при реализации рассматриваемого
способа, измерения производят по
следующей методике. На основе (14) при
разрядке известной емкости С
через определяемое сопротивление R,
можно записать
![]() ,
(17)
,
(17)
![]() ,
(18)
,
(18)
где
![]() и
и
![]() – измеряемые значения напряжения на
конденсаторе в моменты времени t1
и t2
соответственно.
Производя деление (17) на (18), после
преобразований получим:
– измеряемые значения напряжения на
конденсаторе в моменты времени t1
и t2
соответственно.
Производя деление (17) на (18), после
преобразований получим:
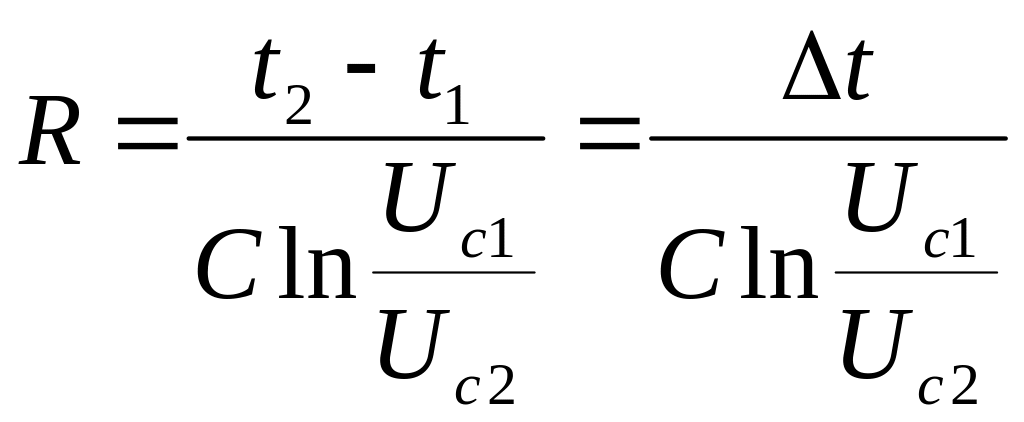 ,
(19)
,
(19)
где
![]() – интервал времени между измерениями
напряжений
и
на емкости в процессе ее разрядки. При
использовании (19) нет необходимости в
измерении Uнач
и точной фиксации момента начала разряда.
– интервал времени между измерениями
напряжений
и
на емкости в процессе ее разрядки. При
использовании (19) нет необходимости в
измерении Uнач
и точной фиксации момента начала разряда.
В «классическом» диэлектрике накопление заряда обусловлено поляризацией диэлектрика во внешнем электрическом поле: положительные концы молекул под действием электростатических сил, создаваемых внешним электрическим полем, поворачиваются к отрицательному электроду, отрицательные концы молекул – к положительному электроду. При этом у электродов в диэлектрике образуется поляризационный заряд по знаку противоположный знаку заряда прилегающего электрода. Поэтому заряд этого типа в диэлектрике называется гетерозарядом (рис. 3).

Рис. 3. Схематический разрез диэлектрика с нижней металлизированной поверхностью
1 – диэлектрик, 2 – слой металлизации, 3 – осажденные на поверхности заряды, 4 – инжектированные заряды (гомозаряды), 5 – поляризационные заряды (гетерозаряды), 6 – компенсационные (индуктированные) заряды
