10. Записать ответ
P
=
11. Сделать в письменном виде выводы, следствия и заключение по результатам работы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется моментом инерции твердого тела?
2. От чего зависит момент инерции твердого тела?
3. В каких единицах в СИ измеряется момент инерции?
4. От чего зависит период крутильных колебаний?
5. Записать дифференциальное уравнение гармонических крутильных колебаний.
1. Савельев И.В. Курс общей физики. - М.: Наука, 1977, Т. 1. - С. 153-145.
2. Гусев Г.В., Буркова Л.А. Учебное пособие. Обработка и анализ результатов лабораторного физического эксперимента. - СПб.: СПГУТД, 1995.
Составители доц. Л.А.Тугуши, проф. Б.М.Тараканов,
доц. Г.В.Гусев
Лабораторная работа № 1 изучение стоячих волн в натянутой струне
Целью настоящей работы является исследование собственных колебаний струны методом резонанса, а также определение собственной частоты и скорости распространения поперечных волн при различных силах натяжения струны.
В натянутой, закрепленной на концах струне при возбуждении возникают стоячие волны, появление которых нетрудно объяснить с позиций интерференции когерентных упругих волн, распространяющихся в струне. Стоячие волны в струне возникают за счет наложения падающей на преграду (точку закрепления) и бегущей ей навстречу отраженной упругих волн, уравнения которых имеют вид
(1)
(2)
где x - координата произвольно выбранной на струне точки; y1 - смещение этой точки в прямой волне (распространяющейся в положительном направлении Х); y2 - смещение этой точки в отраженной волне (распространяющейся в отрицательном направлении Х); А - амплитуда колебаний; - скорость распространения волны; - циклическая частота колебаний.
Согласно принципу суперпозиции (независимого наложения) отклонения каждой точки струны от положения равновесия будет равно
(3)
или
(4)
Уравнение (4) есть уравнение стоячей волны. Так как
где k - волновое число, то уравнение (4) можно записать в виде
(5)
Из
уравнения (5) видно, что все точки струны
колеблются гармонически, а амплитуда
колебаний
различна и зависит от расположения
точки на струне, т.е. от Х (рис. 1).
Рис. 1
Точки
струны, для которых
,
не испытывают колебаний и называются
узлами
(точки 1, 3, 5 на рис. 1).
Координаты узлов находятся из условия
(6)
где n = 0, 1, 2,
Если
учесть, что
,
то
(7)
Из уравнения (7) видно, что расстояние между соседними узлами равно / 2 (рис. 1), где - длина бегущей волны.
Точки
струны, для которых
,
называются пучностями
(точки 2, 4, 6 на рис. 1).
Координаты пучностей находятся из условия kx = n,
где n = 0, 1, 2, , откуда
(8)
Из (8) видно, что состояние между соседними пучностями равно / 2.
Так как точки закрепления натянутой струны при возбуждении колебаний являются узлами стоячих волн, то в струне возбуждаются колебания лишь таких частот, при которых на длине струны укладывается целое число полуволн.
На рис. 2 представлены последовательные (через четверть периода положения трех струн с установившимися стоячими волнами, частоты которых соответствуют основному тону (n = 1), первому (n = 2) и второму (n = 3) обертонам и определяются из условия
или
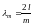(9)
(m = 1, 2, 3, ...)
где
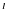- длина струны. Профиль стоячей волны в
любой момент времени представляет собой
синусоиду. Учитывая связь скорости
распространения колебаний
с частотой и длиной волны
=
,
получим
(10)
Опыт показывает, что скорость распространения поперечных колебаний вдоль струны определяется величиной натяжения F струны и линейной плотностью (массой единицы длины) l материала струны, т.е.
Рис. 2
Эта зависимость может быть получена, например, с помощью метода размерностей. В результате зависимость от F и l примет вид
(11)
или
(12)
где d - диаметр струны; v - объемная плотность или просто плотность материала струны.
Подставив значение скорости из (12) (10), получим окончательное выражение для собственных частот колебаний струны:
(13)
Помимо свободных колебаний натянутая струна может совершать вынужденные колебания под действием внешней, периодически меняющейся силы. При таких колебаниях струна будет повторять колебания внешней силы. В условиях резонанса, т.е. при равенстве или близости значений частоты вынуждающей силы, периодической во времени и приложенной к малому участку струны, и одной из собственных частот струны в ней устанавливаются стоячие волны с максимальной амплитудой колебаний. При этом необходимо, чтобы участок приложения вынуждающей силы совпадал с одной из пучностей соответствующей стоячей волны.
ОПИСАНИЕ УСТАНОВКИ И МЕТОДА ИЗМЕРЕНИЯ
Приборы и принадлежности: закрепленная в ящике медная струна с подставкой для грузов; набор разновесов; генератор электрических колебаний; магнит; штангенциркуль; масштабная линейка.
В схеме установки, представленной на рис. 3, струна натягивается горизонтально. Один ее конец закреплен неподвижно, а к другому концу, перекинутому через латунный цилиндр, играющий роль блока, прикреплена чашка с грузами, с помощью которых в струне создается натяжение.
От генератора электрических колебаний на струне подается переменное напряжение. Вдоль струны по подставке может свободно перемещаться магнит, укрепленный на тележке.
Рис. 3
Участок струны с текущей по нему током попадает в поле постоянного магнита, где согласно закону Ампера на него действует сила. Так как ток в струне изменяется по гармоническому закону, то и сила, приложенная к участку струны, также будет изменяться по гармоническому закону. Частота изменения этой силы равна частоте переменного тока, задаваемой генератором электрических колебаний.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Включить генератор звуковых частот.
2. Создать натяжение в струне, поместив на чашку для грузов какой-либо разное1.
3. Измерить диаметр рабочей части в различных участках, а также ее длину.
4. Установив магнит посередине струны и плавно изменяя частоту вращения лимба генератора (при определенном положении переключателя “Множитель”), добиться устойчивых колебаний основного тона. Затем, передвигая магнит, получить устойчивые колебания последующих обертонов. Если амплитуды колебаний очень малы, следует увеличить выходное напряжение на генераторе.
5. Записать в таблицу в порядке возрастания значения частот звукового генератора, при которых на струне устанавливаются стоячие волны. Вычертить профили стоячих волн.
6. Изменить первоначальное натяжение струны. В результате этого изменить скорость распространения поперечных колебаний и набор собственных частот. Провести измерения согласно п. 4 и 5 при других натяжениях. Рекомендуется варьировать натяжение струны в пределах от 50 до 250 г.
7. По формуле (13) рассчитать значения собственных частот колебаний струны при различных ее натяжениях. Вычисленные таким образом значения частот занести в таблицу и сопоставить их со значениями, полученными экспериментально. Объяснить расхождения.
8. Используя значения m , полученные путем отсчета по лимбу генератора для каждого натяжения струны, и формулу (10), определить экспериментальное значение скорости распространения поперечных колебаний .
9. По формуле (12) рассчитать скорости распространения поперечных колебаний для каждого натяжения струны.
10. Найти погрешность измерений.
11. По полученным данным построить график зависимости квадрата скорости распространения колебаний от натяжения струны. На этом же чертеже построить график теоретической зависимости квадрата скорости от натяжения.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Каковы условия возникновения стоячих волн?
2. Перечислить основные особенности стоячей волны.
3. Написать уравнение стоячей волны.
4. Какие точки Среды называются пучностями стоячей волны?
5. Какие точки Среды называются узлами стоячей волны?
6. Какое условие накладывается на частоту свободных колебаний в закрепленной струне?
7. От каких параметров зависит скорость распространения поперечных колебаний в струне?
1. Савельев И.В. Курс общей физики, Т. 2. - М.: Главная редакция физ.-мат. лит., 1982. - С. 289-292.
2. Физический практикум/ Под ред. проф. В.И.Ивероновой. М.: Гос.изд-во технико-теорет. лит., 1961. - С. 101-104.
3. Гусев Г.В., Буркова Л.А. Учебное пособие. Обработка и анализ результатов лабораторного физического эксперимента. - СПб.: СПГУТД, 1995.
Составители проф. Б.М. Тараканов, доц. А.Ю. Пастухов