
- •Содержание
- •10. Записать ответ 32
- •7. По формуле 63
- •Лабораторная работа № 4 определение момента инерции тела при помощи крутильных колебаний
- •Лабораторная работа № 30 определение момента инерции твердго тела и проверка основного закона динамики вращательного движения
- •Лабораторная работа № 5 проверка закона сохранения энергии
- •Лабораторная работа № 2 определение момента инерции твердых тел методом крутильных колебаний
- •10. Записать ответ
- •Лабораторная работа № 1 изучение стоячих волн в натянутой струне
- •Лабораторная работа № 39 определение скорости звука в воздухе интерференционным методом
- •Лабораторная работа № 10 определение коэффициента линейного расширения полимерных материалов
- •Лабораторная работа № 15 определение коэффициента теплопроводности воздуха
- •Лабораторная работа № 16 определение средней длины свободного пробега и эффективного диаметра молекул
- •Лабораторная работа № 17 определение коэффициента внутреннего трения жидкости методом стокса
- •Лабораторная работа № 18 определение коэффициента вязкости воздуха
- •Лабораторная работа № 13 определение отношения теплоемкостей воздуха методом адиабатического расширения
- •Лабораторная работа № 19 изменение энтропии при изохорическом охладжении воздуха
- •Лабораторная работа № 20 изменение энтропии при нагревании и плавлении твердых тел
- •Лабораторная работа № 38 измерение молекулярной теплоемкости твердого тела
- •Лабораторная работа № 22 экспериментальная проверка закона сохранения и превращения энергии
- •( И подставляются в (1.6) в радианах).
- •Лабораторная работа № 25 экспериментальная проверка теоремы гюйгенса-штейнера
- •Описание теоретической части работы
- •Теорема гюйгенса-штейнера
- •Методика измерения
- •Контрольные вопросы
- •Лабораторная работа № 26 определение плотности сыпучих и пористых тел
- •Описание установки
- •Цель работы
- •Порядок выполнения работы
- •Табличные данные
- •Правила работы в лаборатории
Теорема гюйгенса-штейнера
Найдем связь между моментами инерции тела относительно двух различных параллельных осей. Пусть эти оси О и А перпендикулярны к плоскости рис. 1 и пересекают ее в точках О и А.
Разобьем
мысленно тело на элементарные массы
dm. Радиусы- векторы одной из них,
проведенные от осей О и А и параллельные
плоскости рисунка, обозначим
 соответственно, тогда
соответственно, тогда
 .
Следовательно,
.
Следовательно,

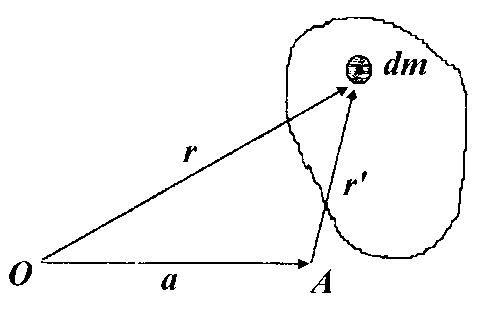
Рис.2
Интеграл
слева есть момент инерции
 тела относительно оси А, первый интеграл
справа - момент инерции относительно
оси О. Таким образом,
тела относительно оси А, первый интеграл
справа - момент инерции относительно
оси О. Таким образом,
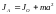
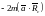 (5)
(5)
Последний интеграл можно представить в виде
 ,
,
где
 -радиус
- вектор центра масс С тела относительно
оси О. Пусть ось О проходит через центр
масс С тела. Тогда
=0,
и (5) упрощается, принимая вид формулы
-радиус
- вектор центра масс С тела относительно
оси О. Пусть ось О проходит через центр
масс С тела. Тогда
=0,
и (5) упрощается, принимая вид формулы
 , (6)
, (6)
в которой
 обозначили через
обозначили через
 Jс
- момент инерции относительно центра
масс тела. Это соотношение называется
теоремой Гюйгенса- Штейнера. Момент
инерции тела относительно какой-либо
оси равен моменту инерции его относительно
параллельной оси, проходящей через
центр масс, сложенному с величиной
Jс
- момент инерции относительно центра
масс тела. Это соотношение называется
теоремой Гюйгенса- Штейнера. Момент
инерции тела относительно какой-либо
оси равен моменту инерции его относительно
параллельной оси, проходящей через
центр масс, сложенному с величиной
 ,
где
,
где
 - расстояние между осями.
- расстояние между осями.
ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА
ТЕОРЕМА ГЮЙГЕНСА-ШТЕЙНЕРА
Из формулы
(4) следует, что период колебаний
математического маятника связан с его
моментом инерции, который, как это видно
из теоремы Гюйгенса-Штейнера (6) зависит
от расстояния между центром масс маятника
и его точкой подвеса (отметим, что d
=
 ).
Поэтому, если взять математический
маятник с известным моментом инерции
Jc , то отношение периодов
колебаний для различных d можно рассчитать
по формуле
).
Поэтому, если взять математический
маятник с известным моментом инерции
Jc , то отношение периодов
колебаний для различных d можно рассчитать
по формуле
 =bрас. (7)
=bрас. (7)
С другой стороны, величина b находится экспериментально из измерений периодов колебаний физического маятника с Jc для различных d. Совпадение рассчитанного значения b с измеренным экспериментально в пределах доверительной погрешности будет указывать на справедливость теоремы Гюйгенса-Штейнера.
Методика измерения
В работе используется цилиндр с моментом
инерции
работе используется цилиндр с моментом
инерции
 ,
где m - масса цилиндра, R - его
радиус. В цилиндре параллельно его оси
просверлены отверстия на различном
расстоянии d от его оси симметрии
рис. 3.
,
где m - масса цилиндра, R - его
радиус. В цилиндре параллельно его оси
просверлены отверстия на различном
расстоянии d от его оси симметрии
рис. 3.
R
d1
d2







Рис. 3
Цилиндр одевается на расстоянии d1 на стержень, закрепленный на штативе. Приводится в колебательное движение и измеряется период колебаний T1 (50.-.70 колебаний). Затем берется расстояние d2 и измеряется период T2. Находится экспериментальное отношение T1/T2 = bэкс.. Это значение сравнивается с вычисленным по формуле

 . (8)
. (8)
РАСЧЕТ ДОВЕРИТЕЛЬНОЙ ПОГРЕШНОСТИ
Для того, чтобы вывести формулу погрешности для bрас., необходимо взять дифференциал от выражения (8) по трем переменным: d1, d2, R


 (9)
(9)
Экспериментальная погрешность находится следующим образом:
 (10)
(10)
Расчет d1, d2, R, t., а также доверительной вероятности P производить в соответствии с теорией погрешностей.
Контрольные вопросы
1. Что такое момент инерции тела?
2. Сформулируйте теорему Гюйгенса-Штейнера.
3. Увеличится ли энергия маховика, если сместить ось вращения параллельно его оси симметрии?
4. Почему балансируют колеса машин?
1. Савельев И.В. Курс общей физики. Механика. Молекулярная физика. - М.: Наука. 1982. Т. 15
2. Яворский Б.М., Детлаф А.А. Справочник по физике.-М.: Наука, 1971. - С.71-72.
3. Сивухин Д.В. Общий курс физики. Механика. - М.: Наука. 1979.
4. Гусев Г.В., Буркова Л.А. Учебное пособие. Обработка и анализ результатов лабораторного физического эксперимента. - СПб.: СПГУТД, 1995.
Составитель проф. К.Г. Иванов
