84

Определение динамического коэффициента вязкости

Определение коэффициента поверхностного натяжения

(Лабораторные работы №№7,8)

Литература

1.  1  9.1 - 9.6.

2.  2  § 53, § 54.

3.  5  лаб. раб. № 13, 14, 16.

Вопросы входного контроля

1. Какие режимы течения жидкости существуют?

2. Объясните возникновение силы внутреннего трения.

3. Напишите уравнение Ньютона для течения вязкой жидкости.

4. Как зависит вязкость жидкости от температуры?

5. Что такое ньютоновские и неньютоновские жидкости?

6. Запишите формулу Пуазейля, проанализируйте ее.

7. Выведите формулу для определения вязкости вискозиметром.

8. Какие силы возникают при движении тела в вязкой среде?

9. Выведите формулу для определения вязкости по методу Стокса.

10. Назовите единицы измерения вязкости.

11. Какое значение имеет определение вязкости биологических жидкостей в медицине?

12. Каковы причины возникновения поверхностного натяжения жидкостей?

13. Чем отличаются друг от друга силы поверхностного натяжения и силы молекулярного давления?

14. Почему на космических кораблях шарообразную форму принимают жидкости даже большей массы, чем капля?

15. Что характеризует коэффициент поверхностного натяжения жидкости?

16. Как зависит коэффициент поверхностного натяжения от температуры и какова причина этой зависимости?

17. Почему мокрые волосы слипаются?

18. Почему некоторые новые ткани после стирки садятся?

19. Какое значение имеет изучение поверхностного натяжения для медицины?

Краткая теория

К жидкостям относятся вещества, которые по своим свойствам занимают промежуточное положение между газами и твердыми телами. Жидкие среды составляют наибольшую часть организма, их перемещение обеспечивает обмен веществ и снабжение клеток кислородом, поэтому механические свойства и течение жидкостей представляют собой интерес для медиков и биологов.

Из механических свойств жидкостей для медицины наиболее важными являются вязкость и поверхностное натяжение.

Вязкость жидкости

Вязкость имеет большое значение в природных, особенно биологических процессах, а также в различных областях технологии и при исследовании гидродинамических процессов.

При движении жидкости отдельные слои ее воздействуют друг на друга с силами, касательными к слоям. Это явление называют внутренним трением или вязкостью. Обусловлено внутреннее трение действием молекулярных сил.

Ньютон установил, что силу трения между слоями можно определить по формуле:

(уравнение Ньютона) (1)

F – сила трения

- градиент модуля скорости.

S – площадь соприкасающихся слоев

- коэффициент динамической вязкости.

Жидкости, состоящие из сложных и крупных молекул (например, растворы полимеров) не подчиняются уравнению Ньютона и называются неньютоновскими. Неньютоновской жидкостью является кровь, т.к. содержит белки и клетки крови.

На вязкость жидкости оказывает большое влияние ее состав. Вязкость крови человека в норме колеблется от 4 до 5 мПас, при патологии же она может изменяться от 1,7 до 22,9 мПас. Она зависит от концентрации ее компонентов: воды, минеральных солей, белков и др.

Следовательно, вязкость крови имеет диагностическое значение. При некоторых инфекционных заболеваниях вязкость крови увеличивается, а при туберкулезе – уменьшается. Вязкость зависит от природы жидкости, от температуры.

С увеличением температуры вязкость жидкостей уменьшается, т.к. уменьшается взаимодействие между молекулами, возрастает подвижность молекул, уменьшается время «оседлой жизни» молекул, называемое временем релаксации.

Для медицины представляет интерес течение вязкой жидкости по трубам, т.к. кровеносная система состоит в основном из цилиндрических сосудов разного диаметра.

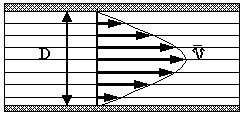
Рис. 1.

Вследствие симметрии ясно, что в трубе частицы текущей жидкости равноудаленные от оси, имеют одинаковую скорость. Наибольшей скоростью обладают частицы, движущиеся вдоль оси трубы. Слой, находящийся в контакте со стенкой трубы, неподвижен. Примерное распределение скорости частиц в сечении трубы показано на рис. 1.

Рассмотренное слоистое течение жидкости называется – ламинарным. Увеличение скорости течения вязкой жидкости вследствие неоднородности давления по поперечному сечению трубы создает завихрение и движение становится вихревым или турбулентным. При турбулентном течении скорость частиц в каждом месте непрерывно и хаотически меняется, движение является нестационарным.

Характер течения жидкости по трубе зависит от свойств жидкости, скорости ее течения, размеров трубы и определяется числом Рейнольдса.

(2)

Если R_e  R_{е крит}, то движение турбулентное.

Для гладких цилиндрических труб R_{е крит}  2300. Так как число Рейнольдса зависит от вязкости и плотности жидкости, то удобно ввести их отношение:

- кинематическая вязкость,

тогда (3)

Единица кинематической вязкости в «СИ» = 1м²/с.

Кинематическая вязкость полнее, чем динамическая учитывает влияние внутреннего трения на характер течения жидкости.

Вязкость проявляется при движении не только жидкости по сосудам и тел в жидкости. При небольших скоростях в соответствии с уравнением Ньютона сила сопротивления движущемуся телу пропорциональна вязкости жидкости, скорости движения тела и зависит от формы и размеров тела.

Наиболее простой формой тела является cфера. Для сферического тела (шарик) зависимость силы сопротивления при его движении в сосуде с жидкостью выражается формулой (законом) Стокса.

(4)

r – радиус шарика

- скорость движения

- коэффициент динамической вязкости.

Существуют различные методы определения коэффициента динамической вязкости. В данной работе вязкость определяется:

1. с помощью вискозиметра Оствальда;

2. методом Стокса (метод падающего шарика).

Вязкость крови измеряется вискозиметром Гесса с двумя капиллярами.