
3. Динамика
Задача
1. В
железнодорожных скальных выемках для
защиты кюветов от попадания в них с
откосов каменных осыпей устраивается
«полка» DC.
Учитывая возможность движения камня
из наивысшей точки А
откоса и полагая при этом его начальную
скорость
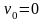 ,
определить наименьшую ширину полки b
и скорость
,
определить наименьшую ширину полки b
и скорость
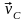 ,
с которой камень падает на нее. По
участку АВ
откоса, составляющему угол α
с горизонтом и имеющему длину l,
камень движется τ
с.
Коэффициент трения скольжения f
камня на участке АВ
считать постоянным, а сопротивлением
воздуха пренебречь.
,
с которой камень падает на нее. По
участку АВ
откоса, составляющему угол α
с горизонтом и имеющему длину l,
камень движется τ
с.
Коэффициент трения скольжения f
камня на участке АВ
считать постоянным, а сопротивлением
воздуха пренебречь.
Дано:
 .
Определить b
и
(рис. 10.3).
.
Определить b
и
(рис. 10.3).
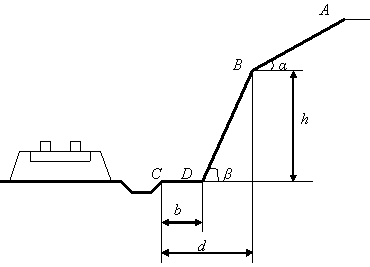
Рис. 10.3
Решение. Задачу разделим на два этапа. Первый – движение камня на участке АВ, второй – движение камня от точки В до С.
Первый
этап. 1. Составление расчетной схемы.
Ось
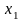 проводим по направлению движения камня,
ось
проводим по направлению движения камня,
ось
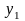 - перпендикулярно к оси
.
Камень принимаем за материальную точку
и показываем ее в текущем положении,
изображаем действующие на камень (точку)
силы: вес
- перпендикулярно к оси
.
Камень принимаем за материальную точку
и показываем ее в текущем положении,
изображаем действующие на камень (точку)
силы: вес
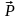 ,
нормальную реакцию
,
нормальную реакцию
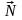 и силу трения скольжения
и силу трения скольжения
 (рис. 10.4).
(рис. 10.4).
2.Выявление начальных условий.
При
 .
.
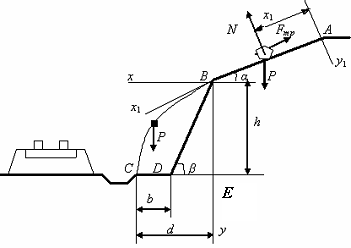
Рис. 10.4
3.Составление дифференциальных уравнений движения точки. Так как точка (камень) движется прямолинейно, то при направлении оси х вдоль траектории получим одно дифференциальное уравнение движения
 ;
;
сила трения
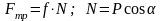 ,
,
тогда
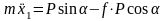 ;
;
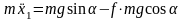 ;
;
 .
.
4.Интегрирование дифференциальных уравнений движения. Интегрируя дифференциальное уравнение дважды, получаем:
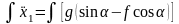 ;
;
 ;
;
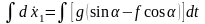 ;
;
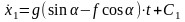 ;
;
 ;
;
 ;
;
 .
.
5.Определение
постоянных интегрирования. Подставим
начальные условия, т.е.
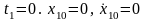 в уравнения:
в уравнения:
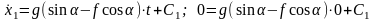 ;
;
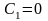 ;
;

 .
.
6.Нахождение неизвестных величин и исследование полученных результатов. После подстановки постоянных интегрирования С1 и С2 получаем уравнение скорости и уравнение движения:
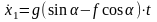 ;
;
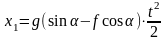 .
.
Для момента времени τ, когда камень покидает участок АВ,
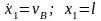 ,
,
т.е.
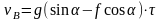 ;
;
 .
.
Умножим первое уравнение на τ/2, после этого разделим его на второе. В результате получим:
 ;
;
 ;
;
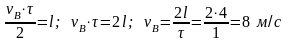 .
.
Второй этап. Движение камня от точки В до точки С.
1.Составление расчетной схемы. Координатные оси покажем так, как это удобно для решения задачи, в нашем случае ось х параллельна горизонтали и проходит через точку В, ось у направляем вниз через точку В. Камень принимаем за материальную точку, показываем ее в текущем положении, изображаем действующую на камень силу тяжести (рис. 10.4).
2.
Выявление начальных условий движения.
При
 :
:
 .
.
3.Составление дифференциальных уравнений движения. Так как движение точки происходит в плоскости ху, то число уравнений движения равно двум:
 .
.
4.Интегрирование дифференциальных уравнений движения. Интегрируем дифференциальные уравнения дважды:
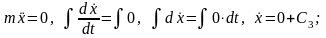 (a)
(a)
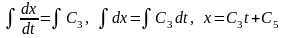 ;
(б)
;
(б)
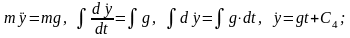 (в)
(в)
 .
(г)
.
(г)
5.
Определение постоянных интегрирования.
Подставляем начальные условия:
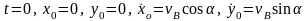 в уравнения (а – г):
в уравнения (а – г):
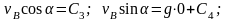
 ,
,
откуда
 .
.
6.Нахождение искомых величин и исследование полученных результатов. После подстановки постоянных интегрирования в уравнения (а –г) получаем следующие уравнения проекций скорости камня:
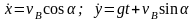
и уравнения его движения
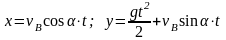 .
.
Уравнение траектории камня найдем, исключив параметр t из уравнений движения:
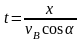 ;
;
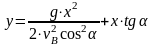 – уравнение
параболы.
– уравнение
параболы.
В
момент падения
 .
Определим d
из уравнения траектории:
.
Определим d
из уравнения траектории:
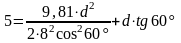 ;
;
 ;
;
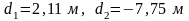 .
.
Так как траекторией движения камня является ветвь параболы с положительными абсциссами ее точек, то d=2,11 м.
Минимальная ширина полки
 .
.
Используя
уравнение движения камня
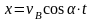 ,
найдем время Т
движения камня от точки В
до точки С
,
найдем время Т
движения камня от точки В
до точки С
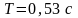 .
.
Скорость камня при падении найдем через проекции скорости на оси координат:
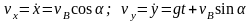
по формуле
 .
.
Для момента падения t=T=0,53 c
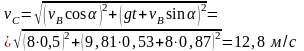 .
.
Скорость камня при падении равна 12,8 м/с.
Задача 2.Груз массой т = 100 кг, подвешенный на невесомом тросе длиной l = 3 м, в результате толчка стал двигаться, как конический маятник, причем трос отклонен от вертикали на угол α = 60° (рис. 50). Определить скорость груза v и силу натяжения троса R.
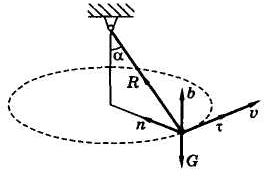
Рис. 50
Решение. Рассматривая груз как материальную точку, применим для описания его движения дифференциальные уравнения в проекциях на естественные оси: касательную τ, нормаль п, бинормаль b (рис. 50).

На груз действуют две силы: сила тяжести G и реакция троса R.
Уравнения движения принимают вид
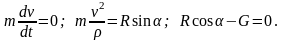
Из первого уравнения следует, что v = const, то есть груз движется равномерно. Из третьего уравнения находим силу натяжения троса (учитывая G = mg)
 .
.
Сила натяжения вдвое больше веса груза.
Из
второго уравнения определим скорость
груза, учитывая, что радиус кривизны
его траектории (окружности в горизонтальной
плоскости)
 .
.
Тогда
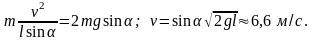
Ответ: v = 6,6 м/с; R = 2 кН.
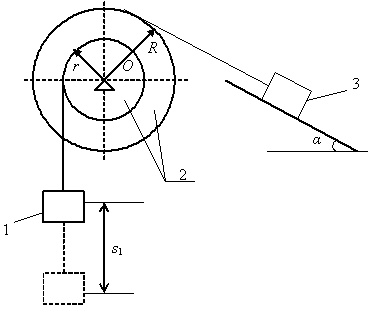
Задача 3. Механическая система под действием сил тяжести приходит в движение из состояния покоя. Учитывая трение скольжения тела 3, пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить скорость и ускорение тела 1 в тот момент, когда пройденный им путь станет равным s (рис. 3.70). В задаче принять:
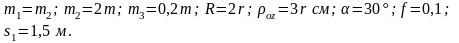
Решение.
На механическую систему действуют
активные силы
 ,
,
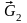 ,
,
 .
Применяя принцип освобождения от связей
системы, покажем реакции шарнирно-неподвижной
опоры 2 и шероховатой наклонной
поверхности. Направления скоростей тел
системы изобразим с учетом того, что
тело 1 спускается.
.
Применяя принцип освобождения от связей
системы, покажем реакции шарнирно-неподвижной
опоры 2 и шероховатой наклонной
поверхности. Направления скоростей тел
системы изобразим с учетом того, что
тело 1 спускается.
Задачу решим, применяя теорему об изменении кинетической энергии механической системы:
 ,
,
где
Т
и
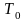 – кинетическая энергия системы в
начальном и конечном положениях;
– кинетическая энергия системы в
начальном и конечном положениях;
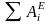 -
алгебраическая сумма работ внешних
сил, приложенных к системе, на перемещении
системы из начального положения в
конечное;
-
алгебраическая сумма работ внешних
сил, приложенных к системе, на перемещении
системы из начального положения в
конечное;
 -
сумма работ внутренних сил системы на
том же перемещении.
-
сумма работ внутренних сил системы на
том же перемещении.
Для рассматриваемой системы, состоящей из абсолютно твердых тел, соединенных нерастяжимыми нитями,
 .
.
Так
как в начальном положении система
покоилась, то
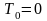 .
Следовательно,
.
Следовательно,
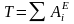 .
.
а)
б)
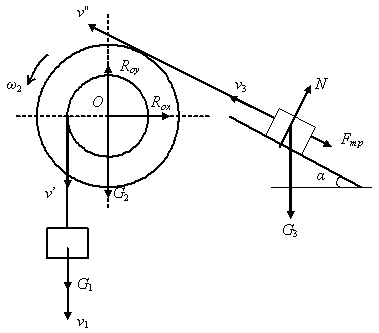
Кинетическая энергия системы представляет собой сумму кинетических энергий тел 1, 2, 3
 .
.
Кинетическая энергия груза 1, движущегося поступательно, равна:
 .
.
Кинетическая энергия блока 2, совершающего вращение вокруг оси Оz, перпендикулярной плоскости чертежа,
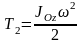 .
.
Кинетическая энергия тела 3 в его поступательном движении
 .
.
Таким образом,
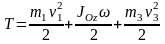 .
.
Выражение
кинетической энергии содержит неизвестные
скорости всех тел системы. Начать
определение необходимо с
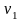 .
Избавимся от лишних неизвестных, составив
уравнения связей.
.
Избавимся от лишних неизвестных, составив
уравнения связей.
Уравнения связей это не что иное, как кинематические соотношения между скоростями и перемещениями точек системы. При составлении уравнений связей выразим все неизвестные скорости и перемещения тел системы через скорость и перемещение груза 1.
Скорость
любой точки обода малого радиуса
 равна скорости тела 1, а также произведению
угловой скорости тела 2 и радиуса вращения
r
равна скорости тела 1, а также произведению
угловой скорости тела 2 и радиуса вращения
r
 .
.
Отсюда выразим угловую скорость тела 2
 .
(а)
.
(а)
Вращательная
скорость любой точки обода блока большого
радиуса
 ,
с одной стороны, равна произведению
угловой скорости блока и радиуса
вращения, а с другой – скорости тела 3
,
с одной стороны, равна произведению
угловой скорости блока и радиуса
вращения, а с другой – скорости тела 3
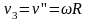 .
.
Подставив значение угловой скорости, получим:
 .
(б)
.
(б)
Проинтегрировав при начальных условиях выражения (а) и (б), запишем соотношение перемещений точек системы:
 .
(в)
.
(в)
Зная основные зависимости скоростей точек системы, вернемся к выражению кинетической энергии и подставим в него уравнения (а) и (б):
 .
.
Момент инерции тела 2 равен:
 .
.
Подставляя значения масс тел и момента инерции тела 2, запишем
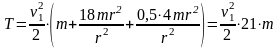 .
.
Определение суммы работ всех внешних сил системы на заданном перемещении.
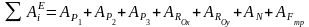 .
.
Работа силы тяжести тела 1
 .
.
Работа
сил
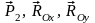 равна нулю, так как эти силы приложены
к неподвижной точке.
равна нулю, так как эти силы приложены
к неподвижной точке.
 .
.
Работа силы тяжести тела 3
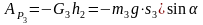 .
.
Работа нормальной реакции тела 3 равна нулю, так как сила перпендикулярна направлению движения
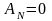 .
.
Работа силы трения скольжения
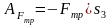 ,
,
так как
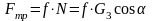 ,
,
тогда
 .
.
Сумма работ внешних сил
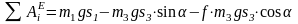 .
.
Подставляя значения масс тел, соотношения перемещений (в) и числовые параметры, запишем:

Теперь
согласно теореме об изменении кинетической
энергии механической системы приравняем
значения Т
и
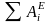
 .
(г)
.
(г)
Скорость тела 1 получим из выражения (г)
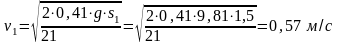 .
.
Ускорение тела 1 можно определить, продифференцировав по времени равенство (г):
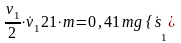 ,
,
где
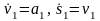 .
.
Тогда
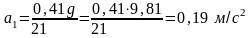 .
.
Задача 4.Грузоподъемная установка (рис. 59) состоит из барабана с осевым моментом инерции J = 4 кгм2 и радиусом r = 20 см, невесомого и нерастяжимого троса и груза массой т = 103 кг, перемещающегося по наклонной плоскости, составляющей угол α = 30° с горизонтом, с коэффициентом трения f = 0,2. Определить величину вращающего момента М, который необходимо приложить к барабану, чтобы его угловое ускорение было равно ε = 5 с–2.
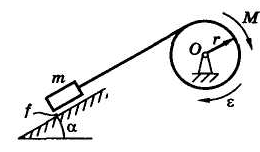
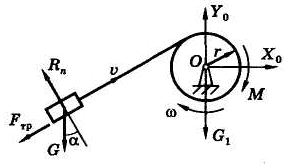
Рис. 59 Рис. 60
Решение. Поскольку рассматривается мгновенное состояние системы, то следует применить теорему об изменении кинетической энергии в дифференциальной форме
 .
.
При условии, что трос нерастяжим и отсутствует проскальзывание троса относительно барабана, система является неизменяемой (внутренние силы не работают), и тогда производная от кинетической энергии будет определяться только мощностями внешних сил:
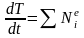 .
.
Кинетическая энергия системы (поступательно движущийся груз и вращающийся барабан, рис. 60)
 .
.
Кинематическая связь, наложенная на скорость груза и угловую скорость барабана, определяется условиями нерастяжимости троса и отсутствием проскальзывания троса относительно барабана: v = ωr. Тогда
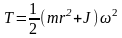 .
.
Выражение
в скобках называется приведенным (к
барабану) моментом инерции:
 кгм2.
кгм2.
Итак, кинетическая энергия системы
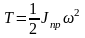 ,
,
а производная от нее по времени
 .
.
дает левую часть записи теоремы.
Рассмотрим действующие в системе внешние силы и их мощности. Сила тяжести барабана G1 и составляющие реакции на его оси Х0 и Y0 будут иметь нулевую мощность (так как равна нулю скорость точки их приложения — точки О). Также равна нулю мощность нормальной реакции груза R,,, поскольку она перпендикулярна скорости груза.
Ненулевую мощность будут иметь только сила тяжести груза G, сила трения Fmp и вращающий момент М:
 ;
;

Тогда (с учетом кинематической связи) сумма мощностей запишется в виде
 .
.
Выражение
в квадратных скобках называется
приведенным (к барабану) вращающим
моментом:
 ,
и тогда правая часть записи теоремы
имеет вид
,
и тогда правая часть записи теоремы
имеет вид
 .
.
Приравнивая
правую и левую части теоремы, получаем
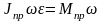 ,
отсюда после сокращения находим
требуемый приведенный вращающий
момент
,
отсюда после сокращения находим
требуемый приведенный вращающий
момент
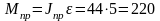 Нм.
Нм.
Теперь
можно найти необходимый вращающий
момент:
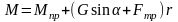 .
Учитывая, что
.
Учитывая, что
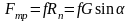 ,
находим
,
находим
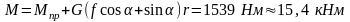 .
.
Ответ: М = 15,4 кНм.
