
- •Практикум по аналитической геометрии
- •Тема 4. Понятие вектора. Действия с векторами. Скалярное, векторное и смешанное произведения векторов. Понятие вектора
- •Координаты вектора на плоскости и в пространстве
- •Простейшие задачи Как найти вектор по двум точкам?
- •Как найти длину отрезка?
- •Действия с векторами в координатах
- •Скалярное произведение векторов
- •Угол между векторами и значение скалярного произведения
- •Скалярный квадрат вектора Что будет, если вектор умножить на самого себя?
- •Угол между векторами
- •Скалярное произведение векторов, заданных координатами в ортонормированном базисе
- •Проверка векторов на ортогональность с помощью скалярного произведения
- •Формула косинуса угла между векторами, которые заданы координатами
- •Проекция вектора на вектор
- •Проекция вектора на координатные оси. Направляющие косинусы вектора
- •Векторное произведение векторов
- •Векторное произведение векторов в координатах
- •Смешанное произведение векторов
Угол между векторами

Если известны длины двух векторов и их скалярное произведение, то можно вычислить косинус угла между данными векторами, а, следовательно, и сам угол.
![]() .
.
Пример
Найти
угол между векторами
и ![]() ,
если известно, что
,
если известно, что ![]() .
.
Решение: Используем
формулу:
 На
заключительном этапе вычислений
использован технический приём –
устранение иррациональности в знаменателе.
В целях устранения иррациональности я
домножил числитель и знаменатель на
На
заключительном этапе вычислений
использован технический приём –
устранение иррациональности в знаменателе.
В целях устранения иррациональности я
домножил числитель и знаменатель на ![]() .
.
Итак,
если ![]() ,
то:
,
то:
![]()
Ответ: ![]()
Не забываем указывать размерность – радианы и градусы.
Пример
Даны ![]() –
длины векторов
,
и
угол между ними
–
длины векторов
,
и
угол между ними ![]() .
Найти угол между векторами
.
Найти угол между векторами ![]() ,
, ![]() .
.
Алгоритм решения:
1)
По условию требуется найти угол между
векторами
и ![]() ,
поэтому нужно использовать формулу
,
поэтому нужно использовать формулу  .
.
2)
Находим скалярное произведение ![]() .
.
3) Находим длину вектора и длину вектора .
4)
Нам известно число ![]() ,
а значит, легко найти и сам угол:
,
а значит, легко найти и сам угол: 
Сделайте самостоятельно и сравните с решением.
Решение:
Найдём скалярное произведение:
 Найдём
длину вектора
:
Найдём
длину вектора
:
 Найдём
длину вектора
:
Найдём
длину вектора
:
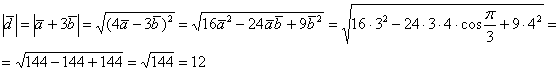 Таким
образом:
Таким
образом:
 Ответ:
Ответ: ![]()
Скалярное произведение векторов, заданных координатами в ортонормированном базисе
В данном разделе рассматриваются только ортонормированные базисы плоскости и пространства.
Скалярное
произведение векторов
и ![]() ,
заданных в ортонормированном
базисе
, выражается
формулой
,
заданных в ортонормированном
базисе
, выражается
формулой ![]()
Скалярное
произведение векторов ![]() ,
заданных в ортонормированном
базисе
, выражается
формулой
,
заданных в ортонормированном
базисе
, выражается
формулой ![]()
То есть, скалярное произведение равно сумме произведений соответствующих координат векторов.
Пример
Найти
скалярное произведение
векторов:
а) ![]() и
и ![]() б)
и
б)
и ![]() ,
если даны точки
,
если даны точки ![]()
Решение:
а)
Здесь даны векторы плоскости. По
формуле ![]() :
:
![]()
б)
Сначала найдём векторы:
 По
формуле
По
формуле ![]() вычислим
скалярное произведение:
вычислим
скалярное произведение:
![]()
Ответ: ![]()
Проверка векторов на ортогональность с помощью скалярного произведения
Векторы
и ![]() ортогональны
тогда и только тогда, когда
ортогональны
тогда и только тогда, когда ![]() .
В координатах данный факт запишется
следующим образом:
.
В координатах данный факт запишется
следующим образом:
![]() (для
векторов плоскости);
(для
векторов плоскости);
![]() (для
векторов пространства).
(для
векторов пространства).
Пример
а)
Проверить ортогональность векторов: ![]() и
и ![]() б)
Выяснить, будут ли перпендикулярными
отрезки
б)
Выяснить, будут ли перпендикулярными
отрезки ![]() и
и ![]() ,
если
,
если ![]()
Решение:
а)
Вычислим их скалярное произведение:
![]() ,
следовательно,
,
следовательно, ![]()
б)
Найдём векторы:

Вычислим
их скалярное произведение:
![]() ,
значит, отрезки
и
не
перпендикулярны.
,
значит, отрезки
и
не
перпендикулярны.
Ответ: а)
,
б) отрезки ![]() не
перпендикулярны.
не
перпендикулярны.
Формула косинуса угла между векторами, которые заданы координатами
Косинус
угла между векторами плоскости
и ![]() ,
заданными в ортонормированном
базисе
, выражается
формулой:
,
заданными в ортонормированном
базисе
, выражается
формулой:
![]() .
.
Косинус
угла между векторами пространства
,
заданными в ортонормированном
базисе
, выражается
формулой:
![]()
Пример
Даны
три вершины треугольника ![]() .
Найти
.
Найти ![]() (угол
при вершине
(угол
при вершине ![]() ).
).
Решение:
 Требуемый
угол
помечен
дугой. Угол
треугольника
совпадает с углом между векторами
и
Требуемый
угол
помечен
дугой. Угол
треугольника
совпадает с углом между векторами
и ![]() ,
иными словами:
,
иными словами: ![]() .
.
Найдём
векторы:

Вычислим
скалярное произведение:
![]()
И
длины векторов:
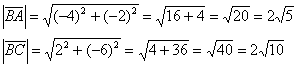
Косинус
угла:

Найдём
сам угол:
![]()
Ответ: ![]()
