10.3. Элементарный автомат (триггерный элемент)
Как уже отмечалось, наиболее типичным примером элементарного автомата и основным последовательностным Элементом является триггер. Термин "триггер" используется для электронных цифровых схем, обладающих двумя устойчивыми внутренними состояниями, которые они могут хранить неограниченно долго, во всяком случае до следующего такта.
Триггер имеет два выходных сигнала Q иQ. Сигнал Q считается истинным или прямым, а сигнал Q - дополнительным или инверсным. Этим сигналам соответствует один из двух уровней напряжения: L или H, и они дополняют друг друга. Выходные сигналы триггера постоянны до тех пор, пока они не будут изменены под воздействием входных сигналов, т.е. триггер имеет два устойчивых состояния (режима): Q = H иQ = L или Q = L и Q = H. Первое из них когда Q = H называется состоянием установки, а второе - состоянием сброса. Предположим, что для триггера используется положительная логика. Тогда состояниям установки и сброса ставятся в соответствие логические состояния 1 и 0.
Существуют различного типа триггерные схемы, в частности, типа: D, T, RS, JK. Для каждого из них имеется однозначное соответствие между входными сигналами и соответствующими переходами состояний триггера. Это соответствие задается таблицей состояний. Приведем, например, условное обозначение RS триггера и его таблицу состояний.
S Q
R Q
Рис.10.5
Таблица состояний RS триггера
Входы
Текущее состояние S = L R = L S = L R = H S = H R = L S = H R = H
Выходы
Q = L Q = H L H L H H L Не опре- делено
Триггер оказывается в состоянии установки, если на вход S подается сигнал высокого уровня, и в состоянии сброса, когда сигнал высокого уровня подается на вход R. Если на оба входа триггера подаются сигналы низкого уровня, то его состояние не меняется, но если на оба входа подаются сигналы высокого уровня, то состояние триггера будет неопределенным.
Логическое поведение триггера, как любого другого автомата, описы-вается логическими таблицами состояний и переходов. Приведем такие таблицы для RS триггера.
Таблица состояний
Входы SR
Текущее 00 01 10 11
состояние Выходы
Q = 0 Q = 1 0 1 0 0 1 1 Не опре- делено
Таблица переходов
Текущее состояние Q Следующее состояние Q S R
0 0 0 d
0 1 1 0
1 0 0 1
1 1 d 0
где d - недоопределенное состояние, т.е. в может равняться либо 0, либо 1.
Приведем вариант реализации RS-триггера на элементах И-НЕ:
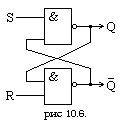
В схеме с N триггерами (например регистр с N триггерами) состояния характеризуются N-разрядным двоичным словом, каждый разряд которого ассоциируется с одним из триггеров. Так как существует 2N различных комбинаций N-разрядного слова, то у данной схемы имеются 2N устойчивых состояний. Очевидно, что состояние выходных сигналов такого регистра зависит не только от того на какие его входы поступили сигналы, но и от того в каком состоянии были его триггера до прихода входных сигналов. Это и является отличительной чертой последовательностных схем от схем первого рода - комбинационных логических схем.
Обычный Т-триггер имеет один счетный вход Т и как все триггера два выхода: Q и Q. Он переключается только при изменении входного сигнала Т с значения 0 на 1.
Синхронизируемый Т-триггер имеет кроме счетного входа Т еще вход СК для синхронизирующего сигнала (синхроимпульса) СИ. Опрокидование триггера происходит в том случае, когда в момент прихода СИ Т = 1, если
T = 0, то СИ не оказывает воздействия на триггер.