Определение

Пусть  — прямоугольная матрица.

Тогда по определению рангом матрицы A является:

• ноль, если A — нулевая матрица;

• число 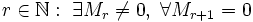, где M_r — минор матрицы A порядка r, а M_{r + 1} — окаймляющий к нему минор порядка (r + 1), если они существуют.

Теорема (о корректности определения рангов). Пусть все миноры матрицы порядка k равны нулю (Mk = 0). Тогда 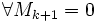, если они существуют.

Связанные определения

• Ранг 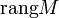матрицы M размера 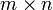называют полным, если .

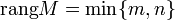• Базисный минор матрицы A — любой ненулевой минор матрицы A порядка r, где .

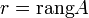  • Строки и столбцы, на пересечении которых стоит базисный минор, называются базисными строками и столбцами. (Они определены неоднозначно в силу неоднозначности базисного минора.)

Свойства

• Теорема (о базисном миноре): Пусть 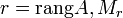 — базисный минор матрицы A, тогда:

  1. базисные строки и базисные столбцы линейно независимы;

  2. любая строка (столбец) матрицы A есть линейная комбинация базисных строк (столбцов).

• Следствия:

• Если ранг матрицы равен r, то любые p:p > r строк или столбцов этой матрицы будут линейно зависимы.

• Если A — квадратная матрица, и 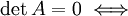, то строки и столбцы этой матрицы линейно зависимы.

• Пусть , тогда максимальное количество линейно независимых строк (столбцов) этой матрицы равно r.

Теорема (об инвариантности ранга при элементарных преобразованиях): Введём обозначение для матриц, полученных друг из друга элементарными преобразованиями. Тогда справедливо утверждение: Если , то их ранги равны.