§ 4. Операции над графами. Подграфы

Рассмотрим основные операции над графами, нужные для их дальнейшего изучения.

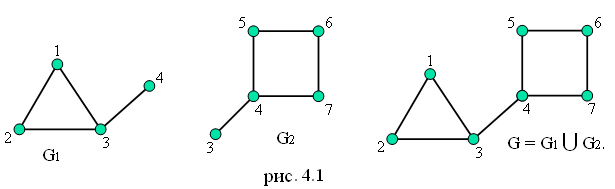
Граф G = <V, H> называется объединением графов G₁= <V₁, H₁> и G₂ = < V₂, H₂> , если V = V₁  V₂ и H = H₁  H₂. В этом случае пишут G = G₁  G₂ (рис. 4.1).

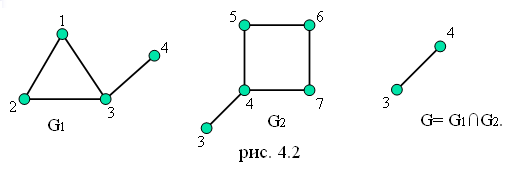
Граф G = <V, H> называется пересечением графов G₁= <V₁, H₁> и G₂ = < V₂, H₂> , если V = V₁  V₂ и H = H₁  H₂. В этом случае пишут G = G₁  G₂ (рис. 4.2).

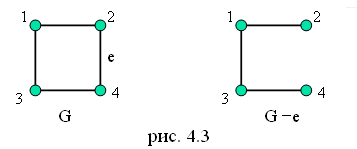
Операция удаления ребра e v из графа G определяется так: граф G^ =G  e имеет те же вершины, что и G и все его ребра, кроме ребра e (рис. 4.3).

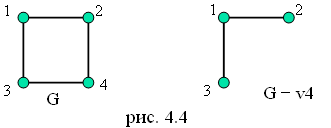
Операция удаления вершины v из графа G определяется так: граф G^ =G  v получается из графа G в результате удаления вершины v и всех ее ребер (рис.4.4).

1

Граф H = <V₁, E₁> называется подграфом графа G = <V, E>, если V₁V и E₁E (рис. 4.5).

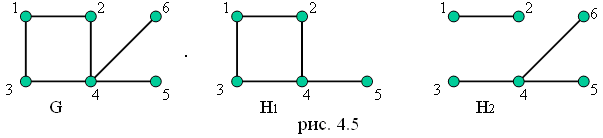
Подграф H называется остовным подграфом графа G, если V₁=V. На рис.4.5 подграф H₂  остовный подграф графа G, а подграф H₁  не остовный.

Подграф H = (V₁, E₁) называется подграфом, порожденным множеством вершин V₁, если множество его ребер E₁ совпадает с множеством всех ребер графа G, оба конца которых принадлежат множеству V₁. Подграф H₁ на рис.4.5  подграф, порожденный множеством {1, 2, 3, 4, 5}.