4.3. Приближенный метод решения задачи (4.1) – (4.2)

Отрезок разбиваем на n равных частей с шагом . Тогда получится сетка .

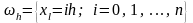Обозначим

Мы знаем, что

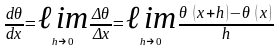
При малых h справедливо соотношение

или

- правая разностная производная, - левая разностная производная.

Аналогично получится приближенная формула

т.е. считаем, что площадь поперечного сечения Q постоянная величина вдоль трубопровода. На основе этих формул из (4.1) получается приближенное неравенство.

Предполагая, что h малая величина составляем равенства

(4.3)

i=1, 2, …, n-1.

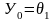, . (4.4)

где .

(4.3) – (4.4) является разностной задачей.

Теорема – 1. Если , то решение разностной задачи (4.3) – (4.4) сходится к решению (4.1) – (4.2) при 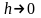и справедливо неравенство

(4.5)

где C- константа, зависящая от начальных данных.

Из (4.5) становится ясно, что при малом h в качестве можно взять решение приближенной задачи (4.3) – (4.4).

4.4. Трехточечная разностная схема. Метод прогонки.

Из (4.3) – (4.4) получаем равенства

(4.6)

где

.

(4.6) – называется трехточечной разностной схемой. Это есть система n-1 линейных алгебраических уравнений c неизвестными. Данная система имеет единственное решение.

Система (4.6) решается методом прогонки. Предполагаем, что решение (4.6) имеет вид

(4.7)

Подставляем его в (4.6). Тогда,

или

(4.8)

Сравнивая (4.7) и (4.8) получим соотношения

(4.9)

Из (4.7) при l = n-1 получим

.

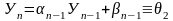Из этого тождества получим

. (4.10)

Из (4.9) и (4.10) определяются все

i = n-2, n -3, …, 0.

После этого из (4.7) используя определяются все

.

Теорема 2. Если и , то метод прогонки является устойчивой. То есть, при реализаций схемы ошибки округления не накапливаются.

В нашем случае оба неравенства выполняются, поэтому метод прогонки является устойчивым.

4.5. Переменные. Блок-схема.

Из определения А_і, В_і, С_і следует равенства

С_і = А_{і -1}, В_і = А_і +А_{і - 1} + а² h²

Поэтому, (4.9) можно переписать в виде

На основе этих формул, при программировании используются массивы

A[0…n], α[0…n-1], β[0…n-1].

Блок-схема

НАЧАЛО

Ввод l, n,θ₀, θ₁, θ₂,

λ(x)

α_n-l =0, β_n-1 = θ₂

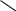
l=n-1, 0,-1

α _l-1 , β _l-1

У_l+1 = α _l У_l + β_i

Вывод У_i

конец

l=0, n-1, 1

Цель лабораторной работы.

С помощью программы установить:

• если длина трубы l достаточно большой, то граничные условия практически не влияют на распределение температуры вдоль трубопровода.

• если длина трубы l короткая, то θ₁ и θ₂ влияет на распределение температуры вдоль трубопровода.

• изучить влияние α и θ₀ на распределение температуры.