- •Казахстанско-британский технический университет факультет информационных технологий кафедра высшей и прикладной математики
- •Рысбайулы б.
- •§1. Интерполирование функций. Сплайны первого и второго порядка.
- •1.1.Сплайн 1-го порядка (кусочно-линейная интерполяция).
- •1.2.Сплайн 2-го порядка s(X).
- •Из последней системы определяются
- •1.3. Расчетные формулы сплайна 2-го порядка.
- •1.4. Переменные и структурная схема расчета.
- •С начало труктурная схема расчета.
- •§2. Приближенное вычисление определенного интеграла
- •2.4. Алгоритм вычисления определенного интеграла.
- •Структурная схема расчета.
- •2.5. Фильтрация жидкости и газа
- •2.6. Несобственный интеграл с бесконечными пределами
- •§3. Расчет показателей нефтяного месторождения в законтурной области пласта при упругом режиме.
- •3.1. Постановка задачи.
- •3.2. Математическая модель задачи.
- •3.3.Численные методы решения задачи (3.1) – (3.2).
- •2. Метод Рунге – Кутта второго порядка точности.
- •3. Метод Рунге – Кутта третьего порядка точности.
- •4. Метод Рунге – Кутта четвертого порядка точности.
- •§ 4. Задача теплообмена в трубопроводе нефтеперевозки . Дифференциальные уравнения второго порядка. Краевая задача
- •4.1. Постановка задачи.
- •4.2. Математическая модель.
- •4.3. Приближенный метод решения задачи (4.1) – (4.2)
- •4.4. Трехточечная разностная схема. Метод прогонки.
- •4.5. Переменные. Блок-схема.
- •Блок-схема
- •§ 5. Смешанная краевая задача для уравнения параболического типа. Нестационарный теплообмен при перевозке нефти трубопроводом.
- •5.1. Постановка задачи
- •5.2. Математическая модель.
- •Систему линейных алгебраических уравнений перепишем в виде
- •7.4. Расчетная схема.
- •7.5. Переменные и блок – схема.
- •Блок-схема
- •7.6. Задания для лабораторной работы.
- •§8. Обратная задача для уравнения теплопроводности.
- •Численная реализация
- •Связь между уравнениями
- •Литература
- •Дополнительная литература
4. Метод Рунге – Кутта четвертого порядка точности.
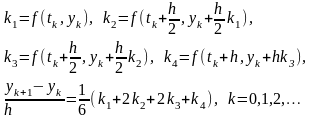
Погрешность метода.
 ,
где
,
где
 – константа, зависящая от начальных
данных и не зависящая от к.
– константа, зависящая от начальных
данных и не зависящая от к.
Замечание: Метод Рунге-Кутта также применяется, если неизвестная функция является вектором, т.е.
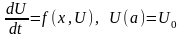 ,
где
,
где
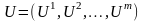 Лекция 7.
Лекция 7.
§ 4. Задача теплообмена в трубопроводе нефтеперевозки . Дифференциальные уравнения второго порядка. Краевая задача
1-го рода.
4.1. Постановка задачи.
Задача
4. Длинный
трубопровод с теплопроводностью λ
(ккал/м.час град.) находится в состоянии
теплового равновесия, т.е. температура
точек трубопровода не изменяется во
времени. Потеря тепла через поверхность
трубопровода в окружающую среду,
температура которой
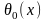 ,
пропорциональна разности температур
с постоянным коэффициентом теплопередачи
α
(ккал/м2.
час град.). Считая температуру θ во всех
точах поперечного сечения трубопровода
постоянной, найти ее зависимость θ
= θ(х) от
координаты, отсчитываемой от какого-либо
конца.
,
пропорциональна разности температур
с постоянным коэффициентом теплопередачи
α
(ккал/м2.
час град.). Считая температуру θ во всех
точах поперечного сечения трубопровода
постоянной, найти ее зависимость θ
= θ(х) от
координаты, отсчитываемой от какого-либо
конца.
4.2. Математическая модель.
Строго говоря, решение этой задачи приводит к дифференциальному уравнению с частными производными, так как температура в поперечном сечений трубопровода не вполне постоянна и является функцией расстояния х и расстояния поверхности стержня.
Однако, если трубопровод
достаточно тонкий и если теплопроводность
его велика, то мы можем без существенной
ошибки пренебречь температурными
градиентами в направлениях перпендикулярных
к оси трубопровода и принять температуру
постоянной в каждой точке поперечного
сечения, перпендикулярного оси Ох. При
таком допущении температура является
функцией только одного независимого
переменного
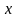 и распределение температуры может быть
описано обыкновенным дифференциальным
уравнением.
и распределение температуры может быть
описано обыкновенным дифференциальным
уравнением.
Пусть длина стержня равна l м, периметр поперечного сечения p м, площадь поперечного сечения Q м2. Исследуем процесс распространения тепла в элементарном отрезке длиной dx на расстоянии х от того конца стержня, температура которого t1. Количество тепла проходящего за время d через сечение трубопровода находящееся на расстоянии х от начало трубопровода, согласно теории теплопередачи, будет равно:
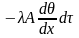
Количество тепла, прошедшее за время d через сечение, находящееся на расстоянии х + dx от начала, будет равна:
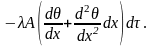
Участок стержня, заключенный между сечениями, отстоящими от начала на расстояниях х и х + dx, вследствие теплопроводности, приобретает за время d количество тепла, равное разности указанных количеств, т.е.:
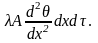
За то же время потеря тепла от этого же участка в окружающую среду будет равна:
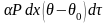
Но так как изучаемый нами процесс является стационарным, то:
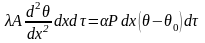
Окончательно мы приходим к следующему дифференциальному уравнению:
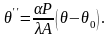
В итоге получена задача:
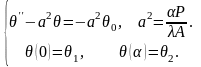
Это уравнение с постоянными коэффициентами. Его общий интеграл будет:
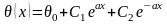
Используя граничные условия, составим систему:
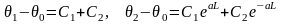
откуда
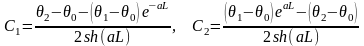
Подставляя значения С1 и С2 получим:
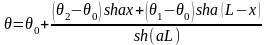
Выделим элемент длины
dх, находящийся на расстояний х
от левого конца, и примем его температуру
равной
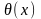 .
За время ∆t через
левую границу этого элемента пройдет
количество тепла
.
За время ∆t через
левую границу этого элемента пройдет
количество тепла
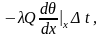
а через правую на расстоянии х+dх от конца
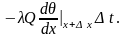
Таким образом, выделенный
участок приобретает за время
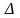 t
количество тепла, равное разности
t
количество тепла, равное разности
 .
.
Вместе с тем потеря тепла этого элемента через поверхности в окружающую среду равна
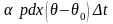 .
.
Вследствие предположения о стационарности процесса эти количества равны, т.е.
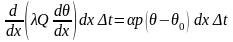
откуда
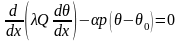 (4.1)
(4.1)
Пусть на обоих концах
стержня поддерживается постоянная
температура
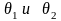 .
Тогда краевые условия имеют вид.
.
Тогда краевые условия имеют вид.
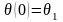 ,
,
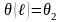 (4.2)
(4.2)
Численный
пример. Пусть
= 10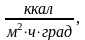
= 300 ккал/мчасград
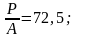 тогда
тогда
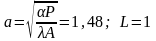
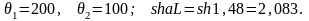
При этом случае получится зависимость