
- •5. Уравнения линий привести к каноническому виду. Построить линии.
- •6. Изобразить линии: а) , б) , в) .
- •6. Изобразить линии: а) , б) , в) .
- •3. Найти угол между прямыми и .
- •6. Изобразить линии: а) , б) , в) .
- •6. Изобразить линии: а) , б) , в) .
- •2. Найти угол между прямыми и .
- •5. Изобразить линии: а) , б) , в) .
Вариант 1
Составить уравнение плоскости, которая проходит через ось Oy и точку M(1,4,–3).
Найти угол между прямыми
 и
и
 .
.
Установить, что три плоскости 2x 4y 5z 21 0, x 3z 18 0, 6x y z 30 0 имеют общую точку и вычислить ее координаты.
Расстояние между директрисами эллипса в 2 раза больше расстояния между его фокусами. Определить эксцентриситет эллипса. Построить эллипс.
Уравнения линий привести к каноническому виду. Построить линии.
а)


2x
4y
1
0, б) 4
9
18y
27
0,
2x
4y
1
0, б) 4
9
18y
27
0,
в) 9 4 18x 16y 43 0, г) 6y 2x 3 0.
6.
Изобразить линии: а)
 ,
б)
,
б)
 ,
в)
,
в)
 .
.
Вариант 2
1.
Составить уравнение плоскости, которая
проходит через точку M(2,–1,1)
перпендикулярно двум плоскостям
 и
и
 .
.
2.
Проверить, лежат ли прямые
 и
и
 в одной плоскости?
в одной плоскости?
3.
Вычислить
расстояние от начала координат до
плоскости, проходящей через три точки
 (–6,1,–5),
(–6,1,–5),
 (7,–2,–1),
(7,–2,–1),
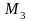 (10,–7,1).
(10,–7,1).
4.
Асимптоты гиперболы имеют уравнения
 ,
а расстояние между фокусами равно 20.
Написать ее каноническое уравнение.
Построить.
,
а расстояние между фокусами равно 20.
Написать ее каноническое уравнение.
Построить.
5. Уравнения линий привести к каноническому виду. Построить линии.
а) 4x 2y 6 0, б) 5 9 30x 18y 9 0,
в) 5 4 16y 36 0, г) 4x y 1 0.
6..
Изобразить линии: а)
 , б)
, б)
 ,
в)
,
в)
 .
.
Вариант 3
1. Составить уравнение плоскости, проходящей через ось Oz и точку M(1,–2,1).
2.
Найти проекцию точки A(1,–3,2)
на плоскость
 .
.
3.
Вычислить расстояние между плоскостями
 и
и
 .
.
4.
Составить уравнение параболы, если даны
ее фокус F(4,3)
и директриса
 .
Построить параболу.
.
Построить параболу.
5. Уравнения линий привести к каноническому виду. Построить линии.
а) 4y 4 0, б) 3 4 18x 8y 5 0,
в) 4 16x 2y 15 0, г) 2x 4y 2 0.
6.
Изобразить линии: а)
 , б)
, б)
 ,
в)
,
в)
 ,
,
Вариант 4
1. Составить уравнение плоскости, которая проходит через точки (7,2,–3) и (5,6,–4) параллельно оси Ox.
2.
Установить, лежит ли данная прямая
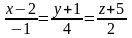 в плоскости
в плоскости
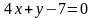 ,
параллельна этой плоскости или пересекает
ее.
,
параллельна этой плоскости или пересекает
ее.
3.
Найти острый угол между плоскостями
 и
и
 .
.
4.
Составить уравнение окружности,
проходящей через точки A(–1,1)
и B(1,–3),
если центр ее лежит на прямой
 .
Построить эту окружность.
.
Построить эту окружность.
5. Уравнения линий привести к каноническому виду. Построить линии.
а) 2x 6y 6 0, б) 9 2x 54y 73 0,
в) 9 4 18x 8y 31 0, г) 2x 4y 5 0.
6. Изобразить линии: а) , б) , в) .
Вариант 5
1.
Составить уравнение прямой, проходящей
через точку пересечения прямой
 и плоскости
и плоскости
 и точку M(3,–3,0).
и точку M(3,–3,0).
2. Вычислить расстояние от точки P(2,–5,7) до прямой, проходящей через точки (5,4,6) и (–2,–17,–8).
3.
Найти угол между прямой
 и плоскостью
и плоскостью
 .
.
4.
Дан эллипс
 .
Найти уравнение гиперболы, вершины
которой находятся в фокусах, а фокусы
– в вершинах данного эллипса. Построить
эллипс и гиперболу.
.
Найти уравнение гиперболы, вершины
которой находятся в фокусах, а фокусы
– в вершинах данного эллипса. Построить
эллипс и гиперболу.
5. Уравнения линий привести к каноническому виду. Построить линии.
а) 2x 6y 6 0, б) 2 3 4x 6y 1 0,
в) 4 8y 0, г) 2x 4y 5 0.
6.
Изобразить линии: а)
 , б)
, б)
 ,
в)
,
в)
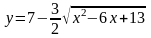 .
.
Вариант 6
1. Составить уравнение плоскости, которая проходит через ось Oz и точку M(2,–3,4)
2.
Составить уравнение прямой, проходящей
через точку M(2,–3,4)
и перпендикулярно прямым
 и
и
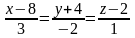 .
.
3.
Доказать, что прямые
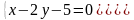 и
и
 пресекаются. Найти точку их пересечения.
пресекаются. Найти точку их пересечения.
4.
Каково будет уравнение параболы
 ,
если ее ось симметрии повернуть на
,
если ее ось симметрии повернуть на
 ;
;
 ;
;
 .
Построить.
.
Построить.
5. Уравнения линий привести к каноническому виду. Построить линии.
а) 4x 4y 1 0, б) 9 4 36x 16y 16 0,
в) 4 9 36y 72 0, г) 2x 6y 11 0.
6.
Изобразить линии: а)
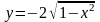 , б)
, б)
 ,
в)
,
в)
 .
.
Вариант 7
1.
Через точку пресечения прямой
 и плоскости
и плоскости
 провести плоскость, перпендикулярную
к данной прямой.
провести плоскость, перпендикулярную
к данной прямой.
2. Составить уравнение плоскости, проходящей через точку M(2,3,–4) и параллельно плоскости YOZ.
3.
При каком значении c
прямая
 параллельна плоскости
параллельна плоскости
 .
.
4. Эллипс касается оси Ox в точке A(4,0) и оси Oy в точке B(0,-3). Составить уравнение этого эллипса, если его оси параллельны осям координат. Построить.
Уравнения линий привести к каноническому виду. Построить линии.
а) 4y 5 0, б) 2 4x 4y 2 0,
в) 2 12x 2y 19 0, г) 2x 3y 8 0.
6.
Изобразить линии: а)
 , б)
, б)
 ,
в)
,
в)
 .
.
Вариант 8
1.
Составить уравнение плоскости, которая
проходит через две точки
(3,0,4)
и
(1,1,0),
перпендикулярно к плоскости
 .
.
2.
Проверить, лежат ли прямые
 и
и
 в одной плоскости.
в одной плоскости.
3.
Найти расстояние от точки P(2,3,–1)
до прямой
 .
.
4.
Найти полуоси, координаты вершин и
фокусов, эксцентриситет, уравнения
директрис и асимптот гиперболы
 .
Построить.
.
Построить.
Уравнения линий привести к каноническому виду. Построить линии.
а) 2x 4y 4 0, б) 3 4 6x 16y 7 0,
в) 4x 4y 3 0, г) 4x 4y 16 0.
6.
Изобразить линии: а)
, б)
 ,
в)
,
в)
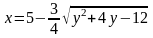 .
.
Вариант 9
1. Составить уравнение плоскости, проходящей через три точки (-6,2,-5), (7,-2,-1), (10,-7,1).
2. Установить, какая из данных прямых
а)
 ;
б)
;
б)
 ;
в)
;
в)
 лежит в плоскости
лежит в плоскости
 ,
какая ей параллельна и какая пересекает
ее.
,
какая ей параллельна и какая пересекает
ее.
3.
Найти угол между прямыми
 и
и
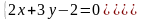 .
.
4. Найти центр и радиус окружности, проходящей через точки A(-1,5), B(-2,-2), C(5,5). Построить.
Уравнения линий привести к каноническому виду. Построить линии.
а) 6x 2y 6 0, б) 4 3 16x 6y 7 0,
в) 4 4x 8y 4 0, г) 4x 2y 5 0.
6.
Изобразить линии: а)
 , б)
, б)
 ,
в)
,
в)
 .
.
Вариант 10
1. Составить уравнение плоскости, которая проходит через точки (3,-2,4) и (2,0,1) параллельно оси Oy.
2.
Через точки
(1,-1,0)
и
(0,3,-12)
провести прямую. Найти точку пересечения
плоскости
 с этой прямой.
с этой прямой.
3. Вычислить расстояние от точки P(-1,1,-2) до плоскости, проходящей через точки (1,-1,1), (-2,1,3), (4,-5,-2).
4. Эллипс касается оси Ox в точке A(0,5) и пересекает ось Oy в точках B(5,0) и C(11,0). Составить уравнение этого эллипса, если его оси параллельны осям координат. Построить его.
Уравнения линий привести к каноническому виду. Построить линии.
а) 6x 4 0, б) 9 4 54x 45 0,
в) 9 54x 72 0, г) 2x 4y 5 0.
6.
Изобразить линии: а)
 , б)
, б)
 ,
в)
,
в)
 .
.
Вариант 11
1. Из точки P(-1,-1,4) опущен на плоскость перпендикуляр. Его основание - точка Q(2,1,3). Составить уравнение этой плоскости.
2.
Составить уравнение плоскости, проходящей
через прямую
 и точку M(2,-2,1).
и точку M(2,-2,1).
3.
Найти расстояние от точки P(1,-1,-2)
до прямой
 .
.
4.
Найти угол между прямой
 и плоскостью
и плоскостью
 .
.
Уравнения линий привести к каноническому виду. Построить линии.
а) 4x 6y 12 0, б) 25 50y 24 0,
в) 5 4 10x 15 0, г) 2x 6y 17 0.
6.
Изобразить линии: а)
 , б)
, б)
 ,
в)
,
в)
 .
.
Вариант 12
Доказать, что прямые
 и
и
 лежат в одной плоскости. Составить
уравнение этой плоскости.
лежат в одной плоскости. Составить
уравнение этой плоскости.Доказать, что прямые
 и
и
 параллельны и найти расстояние между
ними.
параллельны и найти расстояние между
ними.При каких m и l пара уравнений
 и
и
 будет определять параллельные
плоскости. Найти расстояние между
плоскостями.
будет определять параллельные
плоскости. Найти расстояние между
плоскостями.Написать уравнение параболы, зная, что парабола симметрична относительно оси Ox, проходит через точку A(-3,6) и начало координат. Построить.
Уравнения линий привести к каноническому виду. Построить линии:
а) 8x 2y 13 0, б) 9 2x 36y 28 0,
в) 4 5 8x 16 0, г) 2y 4x 5 0.
6.
Изобразить линии: а)
 , б)
, б)
 ,
в)
,
в)
 .
.
Вариант 13
1.
Составить уравнение плоскости, проходящей
через точки
 (2,–1,3)
и
(2,–1,3)
и
 (3,1,2)
параллельно вектору
(3,1,2)
параллельно вектору
 .
.
2.
Составить уравнение плоскости, проходящей
через две параллельные (доказать!) прямые
 и
и
 .
.
3.
Вычислить расстояние от точки
 до прямой
до прямой
 .
.
4.
Найти полуоси, координаты вершин, фокусов
и эксцентриситет эллипса
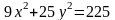 .
Построить.
.
Построить.
Уравнения линий привести к каноническому виду. Построить линии:
а) 2x 8y 8 0, б) 4 4y 0,
в) 9 2x 36y 44 0, г) 8x 3y 22 0.
6.
Изобразить линии: а)
 , б)
,
в)
, б)
,
в)
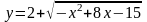 .
.
Вариант 14
1.
Найти точку Q
, симметричную P(3,–4,–6)
относительно плоскости
 .
.
2.
Найти расстояние между двумя параллельными
прямыми
 и
и
 .
.
3.
Найти угол между прямыми
 и
и
 .
.
4.
Определить координаты точек пересечения
прямой
 и окружности
и окружности
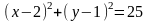 .
Построить.
.
Построить.
5. Уравнения линий привести к каноническому виду. Построить линии:
а) 8y 12 0, б) 3 2 18x 4y 23 0,
в) 6x 4y 1 0, г) 4x 6y 5 0.
6.
Изобразить линии: а)
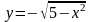 , б)
, б)
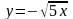 ,
в)
,
в)
 .
.
Вариант 15
1.
Составить уравнение плоскости, которая
проходит через две точки
(1,–1,–2)
и
(3,1,1)
перпендикулярно к плоскости
 .
.
2.
Составить уравнение плоскости, проходящей
через прямую
 параллельно прямой
параллельно прямой
 .
.
3.
При каких значениях A
и B
плоскость
 перпендикулярна к прямой
перпендикулярна к прямой
 .
.
4.
Определить точки пересечения прямой
 и параболы
и параболы
 .
Построить.
.
Построить.
Уравнения линий привести к каноническому виду. Построить линии:
а) 4x 6y 12 0, б) 5 3 10x 12y 2 0,
в) 4 4x 8y 4 0, г) 4x 6y 14 0.
6.
Изобразить линии: а)
 , б)
, б)
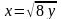 ,
в)
,
в)
 .
.
Вариант 16
1. Составить уравнение плоскости, проходящей через точки (1,3,-2) и (2,2,0) параллельно оси Oz.
2.
Доказать, что прямые
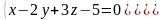 и
и
 лежат в одной плоскости. Составить
уравнение этой плоскости.
лежат в одной плоскости. Составить
уравнение этой плоскости.
3.
Найти угол между прямой
 и плоскостью
и плоскостью
 .
.
4.
Вычислить площадь четырехугольника,
две вершины которого лежат в фокусах
эллипса
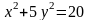 ,
а две другие совпадают с концами его
малой оси.
,
а две другие совпадают с концами его
малой оси.
Уравнения линий привести к каноническому виду. Построить линии:
а) 8y 12 0, б) 2 2x 8y 5 0,
в)
3
2
18x
4y
31
0, г)

2x
8
y
20
0.
2x
8
y
20
0.
6.
Изобразить линии: а)
 , б)
, б)
 ,
в)
,
в)
 .
.
Вариант 17
1.
Составить уравнение плоскости, проходящей
через точку M(1,-2,1)
перпендикулярно к прямой
 .
.
2. Составить уравнения плоскостей, делящих пополам двугранные углы, образованные двумя пересекающимися плоскостями
 и
и
 .
.
3.
При каких значениях m
и C
прямая
 перпендикулярна плоскости
перпендикулярна плоскости
 ?
?
4.
Найти точки пересечения прямой
 и гиперболы
и гиперболы
 .
Построить их.
.
Построить их.
5.Уравнения линий привести к каноническому виду. Построить линии:
а) 6x 8y 24 0, б) 2 12x 8y 32 0,
в) 4 3 8x 12y 4 0, г) 2x 2y 5 0.
6.
Изобразить линии: а)
 , б)
, б)
 ,
в)
,
в)
 .
.
Вариант 18
1.
Найти точку Q
, симметричную точке P(1,3,-4)
относительно плоскости
 .
.
2.
Найти расстояние от точки A(1,3,5)
до прямой
 .
.
3.
При каком значении C
прямая
 параллельна плоскости
параллельна плоскости
 ?
?
4.
Определить точки пересечения двух
парабол
 ,
,
 .
Найти вершины парабол. Построить.
.
Найти вершины парабол. Построить.
Уравнения линий привести к каноническому виду. Построить линии:
а) 8x 6y 24 0, б) 4 8x 24y 48 0,
в) 9 72y 153 0, г) 3x 4y 16 0.
6.
Изобразить линии: а)
,
б)
 ,
в)
,
в)
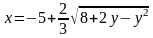 .
.
Вариант 19
1.
Составить уравнение плоскости, которая
проходит через начало координат
перпендикулярно к двум плоскостям
 и
и
 .
.
2.
Составить уравнение плоскости, которая
проходит через точку M(2,-3,3)
параллельно оси Ox
и прямой
 .
.
3.
Найти угол между прямыми
 и
и
 .
.
4.
Найти точки пересечения прямой
 и эллипса
и эллипса
 .
Построить.
.
Построить.
Уравнения линий привести к каноническому виду. Построить линии:
а) 4x 2y 5 0, б) 16 32y 0,
в) 6x 2y 1 0, г) 6x 2y 5 0.
6.
Изобразить линии: а)
 , б)
, б)
 ,
в)
,
в)
 .
.
Вариант 20
1.
Составить уравнение плоскости, проходящей
через прямую пересечения плоскостей
 параллельно вектору
параллельно вектору
 .
.
2.
Даны прямые
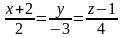 и
и
 .
При каком значении l
эти прямые пересекаются?
.
При каком значении l
эти прямые пересекаются?
3.
Найти угол между прямыми
 и
и
 .
.
4.
Составить уравнение гиперболы, если
известны ее эксцентриситет
 ,
фокус (2,-3) и уравнение соответствующей
директрисы
,
фокус (2,-3) и уравнение соответствующей
директрисы
 .
Построить гиперболу.
.
Построить гиперболу.
Уравнения линий привести к каноническому виду. Построить линии:
а) 8x 12 0, б) 3 4 18x 32y 79 0,
в) 5 4 20x 0, г) 3x 8y 10 0.
6.
Изобразить линии: а)
 , б)
, б)
 ,
в)
,
в)
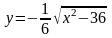 .
.
Вариант 21
Составить уравнение плоскости, проходящей через начало координат, точку A(1,2,3) и перпендикулярно к плоскости
 .
.
2.
Найти расстояние между прямыми
 и
и
 .
.
3.
Найти угол между прямой
 и плоскостью
и плоскостью
 .
.
4.
При каких значениях k
прямая
 пересекает параболу
пересекает параболу
 ;
Построить.
;
Построить.
5. Уравнения линий привести к каноническому виду. Построить линии:
а) 4x 6y 8 0, б) 4 4x 8y 4 0,
в)
4
2
24x
8y
24
0, г)
2x
6y
17
0.
2
24x
8y
24
0, г)
2x
6y
17
0.
6.
Изобразить линии: а)
 , б)
, б)
 ,
в)
,
в)
 .
.
Вариант 22
1.
Составить уравнение плоскости, которая
проходит через точку M(2,1,-1)
перпендикулярно к двум плоскостям
 и
и
 .
.
2.
Составить уравнение плоскости, проходящей
через прямую
 параллельно прямой
параллельно прямой
 .
.
3.
Доказать, что прямая
 принадлежит плоскости
принадлежит плоскости
 .
.
4.
При каких значениях m
прямая
 пересекает эллипс
пересекает эллипс
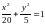 ;
Построить.
;
Построить.
Уравнения линий привести к каноническому виду. Построить эти линии:
а) 6x 5 0, б) 4 9 18y 27 0,
в) 4 4x 24y 28 0, г) 4x 5y 16 0.
