- •Розділ 2. Степені та логарифми.
- •1. Степені. Корінь n-го степеня.
- •2. Властивості степенів.
- •3. Властивості кореня n-го степеня.
- •4. Показникова функція та її графік.
- •5. Поняття логарифмів.
- •6. Властивості логарифмів.
- •Логарифмічна функція та її графік.
- •8. Контрольні питання.
- •9. Приклади для розв’язування.
- •5. Обчислити:
- •6. Обчислити логарифми та знайти значення виразів:
- •7. Розв’язати показникові рівняння:
- •10. Розв’яжіть найпростіші показникові нерівності:
- •11. Розв’яжіть показникові нерівності:
- •12. Знайти область визначення функцій:
- •13. Розв’язати логарифмічні рівняння:
- •15. Розв’яжіть найпростіші логарифмічні нерівності:
- •16. Розв’яжіть логарифмічні нерівності:
Розділ 2. Степені та логарифми.
План
Поняття степені з дійсним показником та кореня n-го степеню
Властивості степенів .(*)
Властивості коренів.(*)
Показникові функція та її графік.(**)
Поняття логарифму.
Властивості логарифмів.(*)
Логарифмічна функція та її графік.(**)
Контрольні питання.
Приклади для розв’язування.
1. Степені. Корінь n-го степеня.
Степенем числа a з натуральним показником n називається добуток n множників, кожний з яких дорівнює а.
![]()
![]() Коренем
n
степеню з числа а
називається таке число b, яке піднесене
до степеню n,
дає підкореневий вираз:
Коренем
n
степеню з числа а
називається таке число b, яке піднесене
до степеню n,
дає підкореневий вираз:
![]()
Степінь з дробовим показником завжди можна представити у вигляді кореню.
Корінь n степеню з числа а завжди можна представити у вигляді степеню з дробовим показником.
![]()
Обчислення степенів з цілим, раціональним ( дробовим ) показниками проводять за правилами, наданими в таблиці.
|
|
|
Степінь з натуральним показником |
|
|
|
Степінь з цілим показником |
|
|
|
Степінь з дробовим показником |
2. Властивості степенів.
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
5. |
|
|
6. |
|
|
7. |
|
|
3. Властивості кореня n-го степеня.
1. |
|
|
2. |
|
|
3. |
|
|
4 |
|
|
5 |
|
|
6 |
|
Корінь з кореня |
7 |
|
Корінь із добутку |
|
|
|
Корінь парного степеня із добутку |
|
|
|
Корінь із частки |
|
|
|
Корінь парного степеня із частки |
|
|
|
Основна властивість коренів |
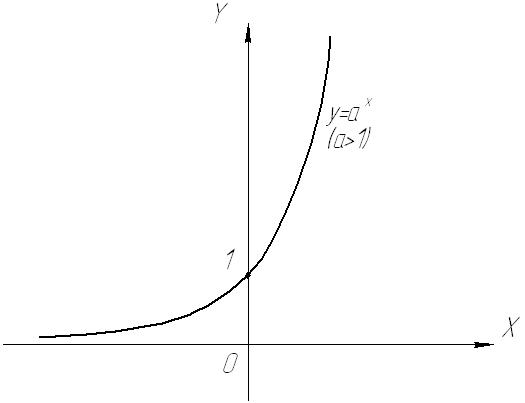
4. Показникова функція та її графік.
Показниковою називається функція, в якій незалежна змінна міститься в показнику степені. Елементарною показниковою функцією є функція:
![]()
В залежності від величини основи а слід розглянути наступні випадки:
|
a>1:
|
|
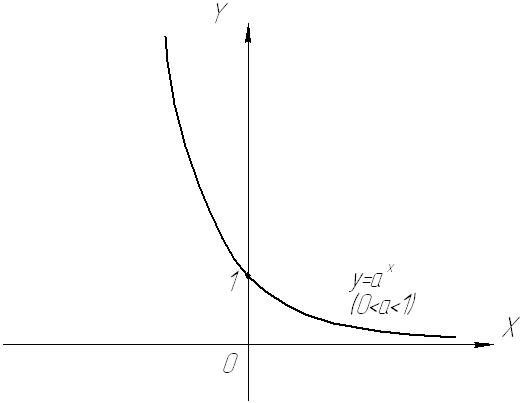
0<a<1: , загального вигляду спадаюча на всій області визначення функція; .
|
Монотонність функції слід враховувати при розв’язуванні показникових нерівностей: знак нерівності не змінюється, якщо основа степені більше одиниці і змінюється на протилежний, якщо основа степені менше одиниці.