
- •9. Проектирование валов.
- •9.2 Разрабртка конструкции вала
- •9.3 Расчет валов на статическую прочность
- •9.4 Уточненный расчет валов на усталостную прочность
- •9.5 Оценка надежности спроектированного вала
- •9.6. Расчет вала на жесткость
- •9.7 Пример расчета быстроходного вала (вал червяка)
- •9.8 Методика расчета валов приводов
9. Проектирование валов.
Проектировочным расчетом определяется диаметр вала в опасном сечении из условия прочности его на изгиб с кручением. Действительные условия работы вала заменяются условными, производится схематизация нагрузок, опор, формы вала. Вследствие такой схематизации расчет валов становится приближенным. Расчетные схемы валов и осей представляют в виде балок на шарнирных опорах. Подшипники, воспринимающие одновременно осевые и радиальные нагрузки, заменяют шарнирно-неподвижными опорами, а подшипники, воспринимающие только радиальные силы – шарнирно-подвижными опорами. Положение опоры принимается посредине ширины подшипника, а в случае сдвоенной опоры – посредине внутреннего подшипника, т.к. в основном, реакции воспринимаются подшипниками, расположенными со стороны нагруженного пролета . Все действующие силы приводятся к оси вала: а ) радиальные силы переносятся в центр вала по линии действия; б ) окружные силы переносятся в центр вала с добавлением крутящего момента; в ) осевые силы переносятся в центр вала с добавлением сосредоточенного изгибающего момента. Как показывают расчеты , осевыми силами при расчете можно пренебречь в силу их малости, учитывая только изгибающий момент от них.
Деформация изгиба валов происходит под действием сил, возникающих в процессе работы той или иной передачи, масс самого вала и насаженных на него деталей. Однако в передачах, разрабатываемых в курсовых проектах, роль масс не велика, поэтому их влиянием можно пренебречь.
9.1 Рассмотрим определение величины и направления сил, действующих в ременных, зубчатых и червячных передачах.
Ременная
передача ( рис. 9.1)

Рис. 9.1
Ременная
передача нагружает валы усилием ![]() (Н),
равным геометрической сумме
(Н),
равным геометрической сумме
натяжений
![]() ветвей ремня
ветвей ремня
![]()
где β – угол схода ветвей.
При
угле обхвата меньшего шкива α![]() 150
150![]() (для плоско – ременной передачи )
(для плоско – ременной передачи )
α 120 (для клиноременной передачи) принимают
![]()
и считают его направленным по линии центров шкивов.
Здесь
![]()
![]() – усилие предварительного натяжения
в ремне, Н ;
– усилие предварительного натяжения
в ремне, Н ;
![]() - напряжение в ремне от предварительного
натяжения ( Н /
- напряжение в ремне от предварительного
натяжения ( Н /![]() )
)
равно 1.5 Н/ - для клиноременных передач и 1.8 Н/ -
для плоскоременных передач;
А - площадь поперечного сечения ремня, ( для клиноременных передач это общая площадь z ремней ).
В цепной передаче и передаче зубчатым ремнем радиальная нагрузка на валы равна
![]()
![]() ,
,
Где - окружное усилие , Н.
Ременная и цепная передачи не меняют полученное направление вращения от электродвигателя.
Цилиндрическая
передача
( рис. 9.2. ) .
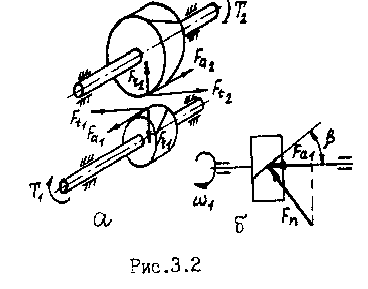
Рис. 9.2
Силы взаимодействия зубьев (рис.9.2.а ) направлены по линии зацепления как общей нормали к рабочим поверхностям зубьев. Силы действующие в зацеплении, принято прикладывать в полюсе зацепления. Силу в зацеплении одной пары зубьев раскладывают:
![]()
![]() - окружные составляющие ( индекс 1-для
шестерни; индекс 2 – для колеса );
- окружные составляющие ( индекс 1-для
шестерни; индекс 2 – для колеса );
![]() -
крутящий момент на валу колеса, Н мм;
-
крутящий момент на валу колеса, Н мм;
![]() -
диаметр делительной окружности колеса,
мм
-
диаметр делительной окружности колеса,
мм
Окружная составляющая силы направлена по касательной к окружности делительного диаметра ( для передач со смещением – начального ) шестерни против вращения , для колеса _ по вращению.
![]() – радиальные составляющие , направленные
по радиусу колес к центрам вращения.
– радиальные составляющие , направленные
по радиусу колес к центрам вращения.
Здесь
αw
– угол зацепления; для передач без
смещения или с ![]() =
0
=
0
![]()
β – угол наклона линии зуба; для прямозубых передач
![]()
![]() - осевые составляющие, направленные
параллельно оси колес в зависимости от
направления вращения и направления
зуба.
- осевые составляющие, направленные
параллельно оси колес в зависимости от
направления вращения и направления
зуба.
Так, полное усилие на зуб Fn ( рис. 9.2, б ) , направленное перпендикулярно линии зуба для шестерни против вращения , для колеса – по вращению , проектирует на ось колеса. Изгибающие моменты от осевых сил на шестерни и на колесе соответственно равны:
![]()
![]()
где
![]() - диаметр делительной окружности шестерни
и колеса.
- диаметр делительной окружности шестерни
и колеса.
Отметим, что на промежуточных валах желательно так назначать направление линии зуба, чтобы осевые составляющие на колесах были направлены в разные стороны и осевые нагрузки на подшипники были наименьшими.
В
прямозубых конических передачах ( рис.
9.3 ) окружные силы определяются по формуле
![]() ,
и направляются аналогично окружным
силам и цилиндрической передаче. Так
как оси шестерни и колеса пересекаются
под углом 90
,
и направляются аналогично окружным
силам и цилиндрической передаче. Так
как оси шестерни и колеса пересекаются
под углом 90![]() то по третьему закону Ньютона попарно
равны между собой
радиальные и осевые составляющие:
то по третьему закону Ньютона попарно
равны между собой
радиальные и осевые составляющие:
![]()
![]()

Рис. 9.3
Сосредоточенные изгибающие моменты от действия осевых сил:
для
вала шестерни - ![]() ;
;
для
вала колеса - ![]() .
.
В
этих формулах α = 20![]() -угол
зацепления;
-угол
зацепления; ![]() -угол
при вершине начального конуса шестерни;
-угол
при вершине начального конуса шестерни;
![]() ,
,
![]() -соответственно
диаметры средних делительных окружностей
шестерни и колеса.
-соответственно
диаметры средних делительных окружностей
шестерни и колеса.
В
червячных передачах
(рис.9.
4)

Рис. 9.4
Благодаря тому , что оси червяка и колеса скрещиваются в пространстве под углом 90 , попарно равны между собой осевые и окружные составляющие. Отметим , что , как и ранее , окружная составляющая на колесе направлена в сторону вращения , а , на червяке – в сторону , противоположную вращению:
![]() ;
;
![]() ;
; ![]() ,
,
где
![]() - крутящий момент на валу червяка , Н мм
;
- крутящий момент на валу червяка , Н мм
; ![]() ,
– соответственно диаметры делительных
окружностей червяка и червячного колеса
; 𝑗 – угол подъёма витков червяка (𝑗=
,
– соответственно диаметры делительных
окружностей червяка и червячного колеса
; 𝑗 – угол подъёма витков червяка (𝑗=
![]() – число заходов червяка , q
– число модулей в делительном диаметре
червяка) ; α = 20
- угол зацепления.
– число заходов червяка , q
– число модулей в делительном диаметре
червяка) ; α = 20
- угол зацепления.
Сосредоточенные изгибающие моменты от действия осевых сил :
для
вала червяка - ![]() ;
;
для
вала червячного колеса - ![]()
Очень важно правильно направить усилия , действующие на вал , ибо , как известно , направление действия сил влияет на значение и направление опорных реакций. Для этого необходимо представить в аксонометрии кинематическую схему привода и редуктора с указанием направления вращения валов и действующих усилий. Следует учитывать , что вал приводного электродвигателя вращается , как правило , по часовой стрелке.
На рис.9.5 представлена кинематическая схема червячно – цилиндрического редуктора , который связан с электродвигателем ременной передачей. Усилия , действующие в цилиндрической передаче , обозначены индексом со штрихом , а в открыто конической передаче – индексом с двумя штрихами.
Порядок
и особенности приближенного расчета
иллюстрируются на примере расчета
тихоходного вала червячно – цилиндрического
редуктора. Так как силы действуют в двух
взаимно перпендикулярных плоскостях
, то и построение эпюр изгибающих моментов
будем производить в двух плоскостях:
вертикальной , где действует окружная
сила в цилиндрической передаче ![]() , радиальная сила
, радиальная сила ![]() и сосредоточенный изгибающий момент
и сосредоточенный изгибающий момент
![]() от открытой конической передачи;
горизонтальной – соответствующей
плоскости разъема редуктора , где
действуют радиальное усилие в
цилиндрической передаче
от открытой конической передачи;
горизонтальной – соответствующей
плоскости разъема редуктора , где
действуют радиальное усилие в
цилиндрической передаче ![]() и окружное усилие на конической шестерне
и окружное усилие на конической шестерне
![]() .
.
Предварительно выполненные расчеты передачи редуктора и построение эскизной компоновки позволили получить следующие величины параметров:
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,

Рис. 9.5
![]()
![]() и размеры , в соответствии с эскизной
компоновкой:
и размеры , в соответствии с эскизной
компоновкой: ![]() ,
,
![]() ,
,
![]() .
.
Вычленим из эскизной компоновки и приложим действующие нагрузки в соответствии со схемой рис.9.5 (см. рис.9.6 , а).
Для
унификации ручного и машинного счета
линейные размеры вала будем проставлять
от начала координат , расположенного
на левом конце рассчитываемого вала:
![]() ,
,
![]()
![]()
Вертикальная плоскость (рис.9.6, б). Определяем реакции на опорах:
![]()
![]() =1216
H .
=1216
H .
![]()
![]()
Поводим проверку равновесия балки в вертикальной плоскости
![]()
Строим эпюру изгибающих моментов в вертикальной плоскости. Изгибающие моменты в характерных точках А, II, B

Рис. 9.6
![]() ;
;
![]() ;
;
![]()
Горизонтальная плоскость (рис.9.6.в) . Определяем реакции на опорах:
![]()
![]()
![]()
![]()
Произведем проверку равновесия балки в горизонтальной плоскости:
![]()
Строим эпюру изгибающих моментов в горизонтальной плоскости (рис.3.6,г) .
На рис.9.7 приведены эпюры крутящих моментов , наиболее характерны для курсового проектирования:
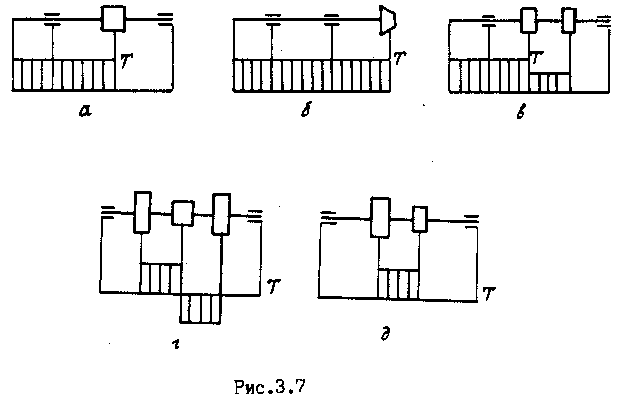
Рис. 9.7
а – быстроходные и тихоходные валы с цилиндрическими и червячными колесами; б – вал
конической
шестерни; ![]() - быстроходный вал с раздвоенной
цилиндрической передачей;
- быстроходный вал с раздвоенной
цилиндрической передачей;
г – промежуточный вал с раздвоенной цилиндрической передачей; д – промежуточный вал редуктора.
Суммарный изгибающий момент в характерных точках по длине вала определяется геометрическим суммированием изгибающих моментов в вертикальной и горизонтальных плоскостях:
![]() ,
,
![]()
![]()
В опасном сечении вала , где действует наибольший суммарный изгибающий момент , определяется приведенный момент , учитывающий совместное действие изгиба и кручения (в нашем примере это сечение под подшипником II)
![]()
(α – коэффициент приведения учитывается , что нормальные напряжения изгиба меняются по симметричному циклу , а , касательные напряжения кручения – по пульсирующему циклу (нереверсивная передача α = 0.59) или симметричному циклу (реверсивная передача α = 1)) .
![]()
Из условия прочности на изгиб с кручением определяют расчетный диаметр вала в опасном сечении:

В
нашем случае примем материал вала –
сталь 45 (по табл.1.1 ![]() )
, тогда допускаемые напряжения на изгиб
по симметричному циклу
)
, тогда допускаемые напряжения на изгиб
по симметричному циклу
[![]() .
.
