
Национальный исследовательский университет - Высшая Школа Экономики Экономический факультет Отделение статистики, анализа данных и демографии Кафедра статистики.
Реферат по теории статистического наблюдения на тему: «Вклад Якоба Бернулли в статистику».
Студент: Малявко Екатерина Гр. 22С
Москва - 2011
Введение.
Якоб Бернулли стал фигурой исключительного значения для теории вероятностей и математической статистики. Но не только он один проявил талант в технических науках. Вся династия швейцарских ученых Бернулли, по крайней мере, восемь её представителей оставили заметный след в истории точных наук.
В истории известны случаи, когда способности гениальных личностей не передаются по наследству их потомкам, но встречаются и счастливые исключения, когда дар переходит от поколения к поколению. Именно такой уникальный феномен представляет собой династия Бернулли. Представители этого рода 250 лет возглавляли кафедры математики и физики Базельского университета.
Купеческая протестантская семья великих математиков бежала из Нидерландов, когда в 1550г. император Карл издал указ против еретиков. В поисках религиозной терпимости они эмигрировали в Швейцарию. Здесь они быстро стали уважаемым семейством.
Первые из этой династии - братья Якоб и Иоганн I - разделяют славу создания современной математики с гениями - Ньютоном и Лейбницем. Лейбниц писал, что анализ бесконечно малых столь же много обязан братьям Бернулли, как и ему самому. Признанием их заслуг являются и научные термины: схема Бернулли, теорема Бернулли, числа Бернулли, закон больших чисел Бернулли и т.п. Более 30 представителей рода обладали талантами, среди них выдающиеся историки, архитекторы, юристы и другие. Но наиболее выдающимися в этой славной семье были Якоб, Иоганн I (в роду Бернулли некоторые имена повторяются из поколения в поколение, поэтому математиков различают как королей) и Даниил. Их достижения стоят на недосягаемой высоте.
Поэтому личность Якоба Бернулли показалась наиболее интересной для анализа.
Биография.
Я коб
родился
27 декабря 1654 года в швейцарском городе
Базель.
Его отец Николай Бернулли был преуспевающим
фармацевтом. Отец хотел, чтобы сын был
священником, поэтому Яков, поступив в
Базельский университет, в основном
изучал теологию и языки. Кроме
государственных языков Швейцарии –
французского, немецкого, итальянского
– и «научного» латинского, Якоб владел
еще английским и греческим. Но больше
всего его привлекала математика, которую
он изучал втайне от отца. Окончив
Базельский университет магистром
философии и богословия в 1671 году, он
начал читать проповеди на немецком и
французском языках. Увлечение математикой
заставило его покинуть этот так
благополучно начатый жизненный путь.
В 1676г. Якоб начинает читать лекции по
экспериментальной физике в Базельском
университете, а через 3 года становится
профессором математики.
В
1677 году совершил поездку во Францию для
изучения идей Декарта, затем в Нидерланды
и Англию, где познакомился с Гуком и
Бойлем.
коб
родился
27 декабря 1654 года в швейцарском городе
Базель.
Его отец Николай Бернулли был преуспевающим
фармацевтом. Отец хотел, чтобы сын был
священником, поэтому Яков, поступив в
Базельский университет, в основном
изучал теологию и языки. Кроме
государственных языков Швейцарии –
французского, немецкого, итальянского
– и «научного» латинского, Якоб владел
еще английским и греческим. Но больше
всего его привлекала математика, которую
он изучал втайне от отца. Окончив
Базельский университет магистром
философии и богословия в 1671 году, он
начал читать проповеди на немецком и
французском языках. Увлечение математикой
заставило его покинуть этот так
благополучно начатый жизненный путь.
В 1676г. Якоб начинает читать лекции по
экспериментальной физике в Базельском
университете, а через 3 года становится
профессором математики.
В
1677 году совершил поездку во Францию для
изучения идей Декарта, затем в Нидерланды
и Англию, где познакомился с Гуком и
Бойлем.
По возвращению из одного из путешествий, он опубликовал свою первую научную работу, посвящённую теории комет. Бернулли утверждал, что кометы – небесные тела с определенными траекториями движения. Статья вызвала критику богословов, так как было заведомо известно, что кометы – знаки божьего гнева, Якобу пришлось согласовать свои научные взгляды с богословской догмой.
В 1684 году женился на Юдит Штупанус, у них родились сын и дочь.
В 1682 году Бернулли получил предложение занять должность проповедника в Страсбурге, но отклонил его, решив в дальнейшем заниматься только физико-математическими науками. В 1683 он начал читать лекции в Базельском университете по экспериментальной физике. В октябре 1686 г. оказывается вакантной должность профессора математики. Успехи Якоба в математике хорошо известны, и Сенат университета единодушно выдвинул на вакантную должность Якоба Бернулли. Вступление в должность состоялось 15 февраля 1687 г.
В 1699 году оба брата Бернулли избраны иностранными членами Парижской Академии наук. Якоб Бернулли умер 16 августа 1705 года в Базеле в возрасте 50 лет. Его вклад в развитие математики трудно переоценить. Благодарные потомки назвали в его честь кратер на Луне.
Вклад в статистику.
Якоб Бернулли был одним из первых исследователей в теории вероятностей, и по этому предмету он написал «Искусство предположения» (Ars conjectandi) – книгу, опубликованную посмертно племянником Николаем Бернулли, в 1713 г. Сочинение состояло из 4 частей, в её первой части перепечатан трактат Гюйгенса «О расчётах в азартной игре». В книге Гюйгенса ещё не было определения и понятия вероятности, она заменялась понятием «количество благоприятных случаев». Вторая часть была посвящена комбинаторике и практическим вариантам её применения. Здесь достаточно полно были изложены известные к тому времени факты о комбинаторике, например формулы:
для числа перестановок из n элементов (
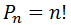 ).
).для числа сочетаний (называемого Якобом Бернулли классовым числом) без повторений (
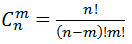 )
и с повторениями (
)
и с повторениями (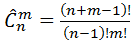 ).
).для числа размещений с повторениями (
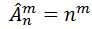 )
и
без повторений (
)
и
без повторений (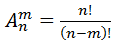 ).
).
Для вывода формул автор использовал наиболее простые и наглядные методы, сопровождая их многочисленными таблицами и примерами. Сочинение Бернулли превзошло работы его предшественников и современников систематичностью, простотой методов, строгостью изложения и в течение XVIII века пользовалось известностью не только как серьёзного научного трактата, но и как учебно-справочного издания.
Якобу Бернулли также принадлежит значительная часть современных понятий в теории вероятностей. Среди них можно найти:
Теорема Бернулли
Якоб доказал теорему Бернулли о биномиальных распределениях — важный частный случай закона больших чисел. Впервые она была опубликована в труде “Искусство предположений”. Первоначальные её доказательства требовали сложных математических средств, лишь в середине XIX века Пафнутий Львович Чебышев нашёл необычайно изящное и краткое её доказательство. Точная формулировка теоремы Бернулли такова: если при каждом из п независимых испытаний вероятность некоторого события равна р, то вероятность того, что частота т/п появления события удовлетворяет неравенству |т/п—р|<ε (ε—произвольно малое положительное число), становится сколь угодно близкой к единице при достаточно большом числе п испытаний. Из доказательства Чебышева вытекает простая количественная оценка этой вероятности:
Р {|m/n—р|<ε}>1—р(1—р)/пε2. Теорема Бернулли была обобщена Симеоном Пуассоном, в сочинении которого "Исследование о вероятности суждения" (1837) впервые появился термин "закон больших чисел".
Схема Бернулли
В
книге «Искусство предположения» Якоб
Бернулли кроме всего прочего представил
модель – «схему Бернулли». Под схемой
Бернулли понимают конечную серию
независимых испытаний, в каждом из
которых возможно лишь 2 исхода – «успех»
и «неудача», при этом успех в одном
испытании происходит с вероятностью
![]() ,
а неудача – с вероятностью
,
а неудача – с вероятностью
![]() .
.
Распределение Бернулли
Имя Якоба носит важное в комбинаторике распределение Бернулли. Распределение Бернулли моделирует случайный эксперимент произвольной природы, когда заранее известна вероятность успеха или неудачи. Случайная величина X имеет распределение Бернулли, если она принимает всего два значения: 1 и 0 с вероятностями р и q соответственно. Таким образом:
![]() ,
,
![]()
Принято говорить, что событие {X = 1} соответствует «успеху», а {X = 0} «неудаче». Эти названия условные, и в зависимости от конкретной задачи могут быть заменены на противоположные.
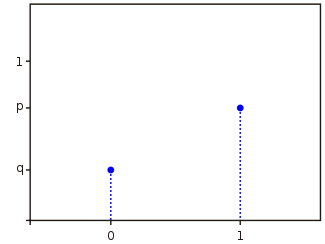
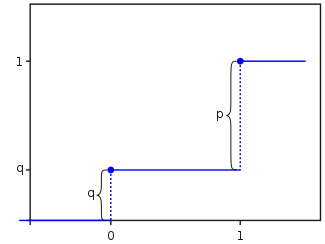
Функция вероятности Функция распределения
Функция
распределения случайной
величины
![]() такова:
такова: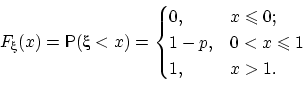
Вариационное исчисление Бернулли
Совместно
с братом Иоганном Бернулли положил
начало вариационному исчислению, разделу
математики, посвящённому нахождению
наибольших и наименьших значений
переменных величин, зависящих от выбора
одной или нескольких функций. Он поставил
задачу о брахистохроне, ставшей одной
из первых задач вариационного исчисления.
Она звучит так: определить форму кривой,
лежащей в вертикальной плоскости, по
которой тяжёлая материальная точка,
двигаясь под действием только одной
силы тяжести и не имеющая начальной
скорости, перейдёт из верхнего положения
А в нижнее положение В за минимум времени.
Эта задача сводится к отысканию функции
у (х), доставляющей минимум функционалу
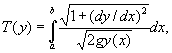
Блуждание Бернулли
Э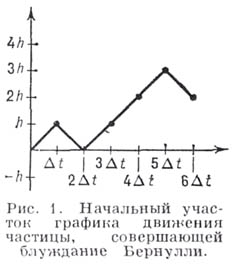 то
случайное блуждание,
порождаемое испытаниями
по схеме Бернулли.
Блуждания Бернулли можно описать в
следующих терминах. Частица движется
по оси х ("блуждает") по решетке
точек вида
то
случайное блуждание,
порождаемое испытаниями
по схеме Бернулли.
Блуждания Бернулли можно описать в
следующих терминах. Частица движется
по оси х ("блуждает") по решетке
точек вида
![]() .
Движение начинается в момент
.
Движение начинается в момент
![]() ,
и положение частицы отмечается только
в дискретные моменты времени
,
и положение частицы отмечается только
в дискретные моменты времени
![]() На каждом шаге координата частицы
увеличивается или уменьшается на
величину h
с вероятностями р
или
На каждом шаге координата частицы
увеличивается или уменьшается на
величину h
с вероятностями р
или
![]() соответственно, независимо от
предшествующего движения. Таким образом,
перемещения в положительном и отрицательном
направлениях ("успехи" и "неудачи")
описываются схемой испытаний Бернулли
с вероятностью успеха, равной р.
Обычно блуждание Бернулли изображают
геометрически, беря ось t
за
ось абсцисс, а ось х
– за
ось ординат (на рисунке показан начальный
участок графика движения частицы,
начинающей блуждание из нуля). Пусть
соответственно, независимо от
предшествующего движения. Таким образом,
перемещения в положительном и отрицательном
направлениях ("успехи" и "неудачи")
описываются схемой испытаний Бернулли
с вероятностью успеха, равной р.
Обычно блуждание Бернулли изображают
геометрически, беря ось t
за
ось абсцисс, а ось х
– за
ось ординат (на рисунке показан начальный
участок графика движения частицы,
начинающей блуждание из нуля). Пусть
![]() – случайная величина, равная перемещению
частицы на j-ом шаге. Тогда
– случайная величина, равная перемещению
частицы на j-ом шаге. Тогда
![]()
![]() образуют
последовательность независимых случайных
величин. Координата блуждающей частицы
в момент
образуют
последовательность независимых случайных
величин. Координата блуждающей частицы
в момент
![]() равна сумме
равна сумме
![]() График даёт наглядное представление о
поведении нарастающих сумм случайных
величин. Этот график можно также
интерпретировать как изменения капитала
одного из игроков в классической задаче
о разорении (именно в связи с этой задачей
были найдены формулы для вероятностей
многих событий в блуждании Бернулли).
График даёт наглядное представление о
поведении нарастающих сумм случайных
величин. Этот график можно также
интерпретировать как изменения капитала
одного из игроков в классической задаче
о разорении (именно в связи с этой задачей
были найдены формулы для вероятностей
многих событий в блуждании Бернулли).
