Решение.

Например, a= a_и ± a = (4,4 ± 0,1)см

b= b_и ± b = (7,4 ± 0,1)см

Задание 2. По результатам измерений вычислите площадь и периметр этого прямоугольника. Полученный результат покажите графически.

Решение.

Полученный в задании 1 результат запишем в виде неравенств:

4,3 см  а  4,5 см; 7,3 см  b  7,5 см

Вычислим площадь, воспользовавшись формулой S=ab:

S = 4,4 см · 7,4 см = 32,56 см²

Вычислим наименьшее (S_min) и наибольшее (S_max) значения площади прямоугольника:

S_min = 4,3 см · 7,3 см = 31,39 см² S_max = 4,5 см · 7,5 см = 33,75 см²

И так, результат вычисления площади прямоугольника, с учётом погрешностей исходных данных в виде неравенства запишется так:

31,39 см² S  33,75 см²

Округлим значения и построим интервал:

Вычислим периметр, воспользовавшись формулой p=2(a+b):

р=2(a+b)=2(4,4см+7,4см)=23,6см

Вычислим наименьшее (р_min) и наибольшее (р_max) значения периметра прямоугольника:

р_min = 2(4,3 см + 7,3 см) = 23,2 см р_max = 2(4,5 см + 7,5 см) = 24 см

И так, результат вычисления периметра прямоугольника, с учётом погрешностей исходных данных в виде неравенства запишется так:

23,2 см р  24 см

Округлим значения и построим интервал:

Задание 3. Тест-драйв автомобиля «Лада Калина» показал, что разгон автомобиля с места до скорости 100 км/ч составляет 14с. Считая движение равноускоренным, определите ускорение автомобиля по формуле a = и вычислите погрешность, если приборная погрешность спидометра составляет 5км/ч, а время измерялось механическим секундомером. Покажите полученный результат графически и, округлив значения, определите погрешность.

Решение.

Используя теорию размерности, вычислим размерность ускорения:

[а] = = M⁰L¹Т^-1T^-1= L¹Т^-2

Переведем скорость и абсолютную погрешность измерения скорости из километров в час, в метры в секунду:

 = 27, 8( ), а ∆ = 1,4 ( )

Вычислим ускорение в системе СИ:

а_и = 2 ( )

Запишем результаты измерения скорости и времени в виде неравенств и вычислим наименьшее (a_min) и наибольшее (a_max) значения ускорения:

26,4 м/с    29,2 м/с; 13 с  t  15 с

а_min = 1,8( ); а_max = 2,2 ( )

И так, результат вычисления ускорения автомобиля с учётом погрешностей исходных данных в виде неравенства запишется так:

1,8 м/с² а  2,2 м/с²

Округлим значения и построим интервал:

Ответ: a = (2,0 0,2)

Занятие 5. Лабораторная работа

Цель работы: выяснить, как зависит период колебаний нитяного маятника от массы груза, длины подвеса и числа колебаний.

Приборы и материалы: штатив, нить длиной около 1 м, грузы, секундомер, измерительная лента.

Ход работы:

1. Закрепите один груз на подвесе и измерьте длину подвеса (нити).

2. Отклоните маятник от положения равновесия на 5-10 см и засеките время двадцати полных колебаний.

3. Результаты измерений занесите в таблицу.

опыт	Масса груза mи ± m, г	Длина подвеса Lи ± L, м	Кол-во колебаний Nи ± N	Время N колебаний tи ± t, с	Период колебаний Tи ± T, с
1
2
3
4

Указание: при использовании лабораторных грузов абсолютную погрешность массы примите ±1г; абсолютную погрешность числа колебаний ±1.

4. Уменьшите число колебаний N в 2 раза. Повторите измерения. Результаты занесите в таблицу.

5. Увеличьте массу груза на подвесе в 2 раза, прикрепив еще один груз. Повторите измерения для десяти полных колебаний. Результаты занесите в таблицу.

6. Уменьшите длину подвеса в два раза. Повторите измерения, не меняя массу грузов и числа колебаний. Результаты занесите в таблицу.

7. Используя формулу T = , вычислите период колебаний маятника во всех четырех случаях и определите интервалы их нахождения.

8. Сравните полученные результаты, используя метод интервалов, и сделайте вывод.

Образец выполнения лабораторной работы

Ход работы:

Результаты измерений и вычислений.

опыт	Масса груза mи ± m, г	Длина подвеса Lи ± L, м	Кол-во колебаний Nи ± N	Время N колебаний tи ± t, с	Период колебаний Tи ± T, с
1	100±1	86,5±0,5	20±1	37,17±0,01	1,8±0,1
2	100±1	86,5±0,5	10±1	18,42±0,01	1,8±0,2
3	200±2	86,5±0,5	10±1	18,90±0,01	1,9±0,2
4	200±2	43,2±0,5	10±1	14,25±0,01	1,4±0,1

1. Вычислим периоды колебаний и интервалы для каждого опыта:

Опыт 1:

T₁ = = = 1,8585 1,9 (с);

T_min = = 1,8 (с); T_max = = 2 (с)

Опыт 2:

T₂ = = = 1,842 1,8 (с);

T_min = = 1,7 (с); T_max = = 2 (с)

Опыт 3:

T₃ = = = 1,89 1,9 (с);

T_min = = 1,7 (с); T_max = = 2 (с)

Опыт 4:

T₄ = = = 1,425 1,4 (с);

T_min = = 1,3 (с); T_max = = 1,6 (с)

2. Представим полученные результаты в виде интервалов:

В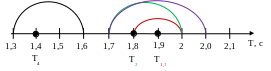 ывод: В первых трех опытах периоды колебаний можно считать равными, следовательно, от числа колебаний и массы груза период колебаний нитяного маятника не зависит. Четвертый опыт показывает, что при уменьшении длины подвеса уменьшается и период колебаний. Также можно заметить, что уменьшение числа колебаний приводит к увеличению погрешности измерений.

Материалы разработаны методистами Новосибирского центра продуктивного обучения

13