Практическое занятие №2

Законы динамики.

Цель работы: научиться определять вид движения, рассчитывать характеристики движения и изображать их на графике.

Приборы и оборудование: линейка, карандаш, задание.

1. Краткие теоретические сведения

I закон Ньютона: существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость неизменной, если на него не действуют другие тела или действие других тел скомпенсировано.

Инерциальные системы отсчета – системы отсчета, в которых выполняется I закон Ньютона.

Любая система отсчета, движущаяся равномерно прямолинейно относительно данной инерциальной системы отсчета, также является инерциальной.

Инертность – свойство тела, заключающееся в том, что тело «сопротивляется» изменению состояния его движения.

Масса – мера инертности тела (инертная масса). Единица массы в СИ: 1 кг.

Сила – векторная физическая величина, являющаяся мерой механического воздействия на материальную точку или тело со стороны других тел или полей. Единица силы в СИ: 1 Н.

Равнодействующая сил (результирующая сила) – сила, которая оказывает на тело такое же действие, как и несколько сил, действующих на тело одновременно.

Силы, приложенные к телу, складываются векторно (геометрически) по правилу параллелограмма или треугольника (если количество сил больше двух).

II закон Ньютона: , где m – масса тела; – ускорение тела; – равнодействующая сил (результирующая сила), действующих на материальную точку (тело).

III закон Ньютона: тела действуют друг на друга с силами, равными по величине (модулю) и противоположными по направлению ( , где – сила, с которой второе тело действует на первое; – сила, с которой первое тело действует на второе).

Особенности сил взаимодействия: 1) одинаковая физическая природа; 2) приложены к разным телам; 3) направлены вдоль одной прямой в противоположные стороны.

Контрольные вопросы

1. Какое свойство тела называют инертностью?

2. Что является мерой инертности тела?

3. Какую массу тела называют гравитационной?

4. Каково соотношение между инертной и гравитационной массой? Какова единица массы в СИ?

5. Как можно измерить массу тела?

6. Какую векторную физическую величину называют силой? Какова ее единица в СИ?

7. Какую силу называют равнодействующей сил (результирующей силой)? Как найти равнодействующую сил, приложенных к телу?

8. Запишите и сформулируйте II закон Ньютона.

9. Сформулируйте III закон Ньютона.

10. Каковы особенности сил взаимодействия?

Образцы решения задач

Задача 1. Какое ускорение сообщит телу массой m = 0,5 кг приложенная к нему сила F = 4Н?

Решение. Воспользуемся вторым законом Ньютона:

– ускорение тела.

Задача 2. К телу массой m = 5 кг, находящемуся на гладкой горизонтальной поверхности, приложены две силы, расположенные в вертикальной плоскости под углом  = 45 друг к другу (рис. 1) и равные по модулю 20 Н, 30 Н. Найти модуль и направление равнодействующей этих сил (результирующей силы), если сила составляет с горизонтом угол . С каким ускорением вдоль горизонтальной поверхности будет двигаться тело?

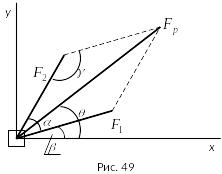
Рисунок 1

Решение. Для определения модуля равнодействующей двух сил воспользуемся теоремой косинусов:

.

.

Тогда

.

.

Определим направление вектора . Для этого вначале определим проекции этого вектора на горизонтальное и вертикальное направление: .

.

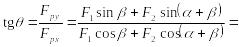
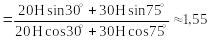
– угол между вектором и горизонтальной осью.

Ответим на последний вопрос задачи:

– ускорение тела в горизонтальном направлении.

Задача 3. Порожний автомобиль, двигаясь из состояния покоя, прошел за первые t секунд путь 30 м. Во сколько раз масса груза, принятого автомобилем, меньше массы самого автомобиля, если при той же силе тяги двигателя груженый автомобиль проходит за те же первые t секунд движения путь 20 м? Силами сопротивления движению пренебречь.

Решение. Ускорение , с которым трогается с места порожний автомобиль, определим из второго закона Ньютона: , где F – сила тяги двигателя автомобиля, m – масса порожнего автомобиля.

Ускорение автомобиля можно определить из кинематической формулы, связывающей путь , пройденный порожним автомобилем за время t, и его ускорение:

.

Приравняем два выражения для ускорения порожнего автомобиля и выразим силу тяги двигателя автомобиля:

.

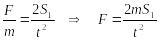Сила тяги двигателя автомобиля останется неизменной и во втором случае: , где – масса принятого груза, – путь, пройденный груженым автомобилем.

Приравняем два выражения для силы тяги автомобиля.

.

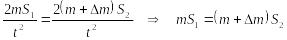Проведем с полученным выражением необходимые математические преобразования:

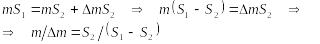
Вычислим результат: .

Масса груза, принятого автомобилем, меньше массы самого автомобиля в два раза.

Задача 4. С какой начальной скоростью тело начало движение вверх по идеально гладкой наклонной плоскости с углом наклона к горизонту  = 30, если на пути = 1,5 м, пройденном телом при подъеме, его скорость уменьшилась в n = 3 раза? За какое время произошло это изменение скорости? Каково максимальное удаление тела от основания наклонной плоскости при подъеме? Через какой отрезок времени и с какой скоростью тело вернется к основанию плоскости?

Решение. На тело, находящееся на гладкой наклонной плоскости, действуют следующие силы: 1) – сила тяжести; – сила реакции опоры (рис. 50).

Складываясь векторно, эти силы создают равнодействующую , направленную вдоль плоскости вниз (рис. 51).

Запишем для движения тела второй закон Ньютона в векторном виде и в проекциях на координатные оси х и у:

(рис. 52).

Получим значения проекций сил на координатные оси:

.

и – модули составляющих и силы тяжести вдоль координатных осей х и у соответственно (рис. 52).

Тогда уравнения движения тела вдоль координатных осей принимают вид:

Ускорение тела, поднимающегося вверх по наклонной плоскости, направлено вниз и равно по модулю .

Проекции на координатную ось х перемещения тела, ускорения, начальной и конечной скорости связаны соотношением:

.

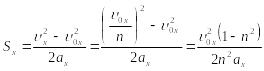Путь, пройденный телом при подъеме, и проекция перемещения на ось х равны между собой: . Начальная скорость тела направлена вверх и поэтому .

Окончательно получим

.

Отсюда

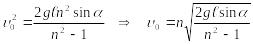– начальная скорость тела (скорость тела у основания наклонной плоскости).

.

– отрезок времени, в течение которого начальная скорость тела уменьшилась в три раза.

.

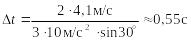Тело будет находиться на максимальном удалении от основания наклонной плоскости в момент времени , когда его скорость станет равной нулю:

Для этого момента времени справедливо соотношение

;

.

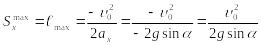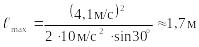В момент возвращения тела к основанию наклонной плоскости проекция его перемещения на ось х становится равной нулю:

.

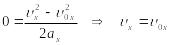Тело возвращается в исходную точку с той же скоростью, с которой начало движение. Направление вектора конечной скорости тела в этот момент времени противоположно оси х, а проекция скорости отрицательна по знаку: .

Отсюда

– время всего движения тела по наклонной плоскости. Как следует из вычислений, , т. е. время подъема тела по плоскости на максимальную высоту и время спуска до основания наклонной плоскости равны между собой.