1.8. Эквипотенциальные линии и поверхности и их свойства.

Линии и поверхности, все точки которых имеют одинаковый потенциал, называются эквипотенциальными. Их свойства непосредственно вытекают из представления работы сил поля и иллюстрируются рис.2.12:

1 ) - работа по перемещению заряда вдоль эквипотенциальной линии (поверхности) равна нулю, т. к. .

2) - силовые линии поля в каждой точке ортогональны к эквипотенциальной линии (поверхности).

Рис.2.12. Иллюстрация свойств эквипотенциальных линий и поверхностей.

1.9. Потенциалы простейших электрических полей.

Из соотношения , определяющего связь между напряженностью и потенциалом электрического поля, следует формула для вычисления потенциала поля:

где интегрирование производится вдоль силовой линии поля; С – произвольная постоянная, с точностью до которой определяется потенциал электрического поля.

Если направление поля совпадает с направлением радиус–вектора ( ), то вычисления можно производить по формуле:

.

Рассмотрим ряд примеров на применение этой формулы.

Пример1. Потенциал поля точечного заряда (рис.2.13).

Рис.2.13. При полагают, что , тогда .

Таким образом, потенциал поля точечного заряда определяется по формуле:

Пример 2. Потенциал поля металлического заряженного шара.

а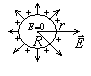 ) Изолированный шар (рис.2.14).

при , т.е. внутри шара = const.

Рис2.14.

Вне шара .

При φ = 0, следовательно, С = 0.

- вне шара.

Для определения используем свойство непрерывности потенциала: при переходе через границу поверхности шара, потенциал не претерпевает скачка. Полагая в последней формуле r =R, находим:

- внутри шара.

б) Заземленный шар (рис.2.15).

.

При , то есть - вне шара.

Рис.2.15. Внутри шара φ(r ≤ 0) = φ₀ = 0.

Разность потенциалов U (рис.2.16) двух точек на силовой линии электрического поля заряженного шара определяется по формуле:

.

Рис.2.16.

Пример 3. Потенциал поля заряженной нити (рис.2.17).

При :

Рис.2.17.

Разность потенциалов U (рис.2.17) двух точек на силовой линии поля заряженной нити:

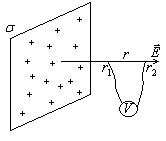
Пример 4. Потенциал поля заряженной плоскости (2.18).

Рис.2.18.

Разность потенциалов U (рис.2.18) двух точек на силовой линии поля заряженной плоскости:

.

Лекция 3 Электростатическое поле в диэлектриках.

1.10. Поляризация диэлектриков. Свободные и связанные заряды. Основные виды поляризации диэлектриков.

Я вление возникновения электрических зарядов на поверхности диэлектриков в электрическом поле называется поляризацией. Возникающие при этом заряды – поляризационными (рис.3.1).

Рис.3.1. Поляризация диэлектрика.

В проводниках (например, металлах) имеются свободные заряды, которые можно разделить (рис.3.2).

Рис.3.2. Разделение свободных зарядов в металле.

В диэлектриках заряды смещаются лишь в пределах отдельных молекул, поэтому их разделить нельзя (рис.3.3). Такие заряды называются связанными.

Рис.3.3. Связанные заряды разделить нельзя.

Различают следующие основные виды поляризации диэлектриков.

1 ) Ориентационная поляризация (полярные диэлектрики).

Молекулы таких веществ уже в начальном состоянии имеют собственный дипольный электрический момент (рис.3.4).

Рис.3.4. Полярная молекула воды.

Электрическим диполем называется система двух связанных между собой равных по величине и противоположных по знаку точечных зарядов. Величина - называется электрическим моментом диполя, - плечо диполя – вектор, направленный от отрицательного заряда к положительному.

В электрическом поле на диполь действует пара сил (рис.3.5), вследствие чего диполь устанавливается (ориентируется) вдоль силовых линий поля.

- момент пары сил, действующий на диполь в электрическом поле.

Рис.3.5. Диполь в электрическом поле.