Задача 3
По направлению к Земле из глубины космоса движется метеоритное облако, скорость которого на значительном удалении от Земли равна Vo=5км/с. Поперечные размеры этого облака много больше диаметра Земли, (толщина облака по направлению движения) составляет h=1000 км, средняя концентрация метеоритов n=0,1 км-3, а центр облака движется в направлении центра Земли. Найти общее число N метеоритов, которые попадут не Землю.
1.Физическая модель
На Землю попадут все метеориты, траектории которых пересекутся с Землей. Одни из них упадут на Землю, двигаясь практически прямолинейно, другие столкнутся
С Землей, потому что их траектории будут искривлены притяжением планеты. Качественно характер траекторий метеоритов, которые упадут на Землю можно изобразить рисунком.
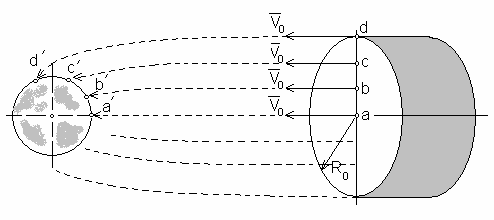
Из рисунка следует, что все метеориты, находящиеся в цилиндрической области облака с радиусом Ro и длиной h, попадут на Землю. Поверхность вращения, которая образуется вращением предельной траектории dd’ вокруг линии аа’, разграничивает две области метеоритов. Те которые лежат внутри этой поверхности - падают на Землю, те которые вне ее - облетают нашу планету и затем летят вспять.
1.Основные понятия
Может показаться, что основным понятием данной задачи будет сила гравитационного взаимодействия метеоритов и Земли, так как она искривляет траектории метеоритов, притягивая их к Земле. Однако решение этой задачи обходится без рассмотрения силы гравитации. Дело в том, что характер траекторий небесных тел, движущихся в поле тяготения силового центра (Солнца или Земли в данной задаче), определяется параметром орбиты и ее эксцентриситетом. Что это за величина можно узнать, заглянув в учебник А. Н. Матвеева “Механика и теория относительности” в разделе “Движение планет и комет”, тогда выяснится, что параметр орбиты и эксцентриситет определяются полной механической энергией и моментом импульса планет и комет. Сохранение же полной механической энергии и момента импульса при движении в потенциальном и центральном силовом гравитационном поле, обеспечивает каждую орбиту планеты или кометы своеобразной родовой меткой: на определенной орбите могут находиться только тела с фиксированными значениями полной механической энергии. Полная механическая энергия Е метеорита в поле тяготения Земли равна:
здесь r – расстояние от центра Земли до метеорита, m и M- масса метеорита и Земли, V - скорость метеорита относительно Земли.
Момент импульса l – метеорита относительно системы отсчета, связанной с центром земли равен:
,
где d - прицельный параметр – кратчайшее расстояние между направлением вектора скорости и центром Земли.
Сохранение полной механической энергии задается условием:
;
сохранение момента импульса
1.Логическая схема решения
Обратимся к рисунку, на котором изображены траектории движения метеоритов. Одна из этих dd’ является особой. Она разделяет траектории, пересекающиеся с Землей, и, проходящие мимо Земли. Применим к этой траектории законы сохранения полной механической энергии для точек d и d’:
здесь R - радиус Земли.
Разрешая эту систему, найдем Ro:
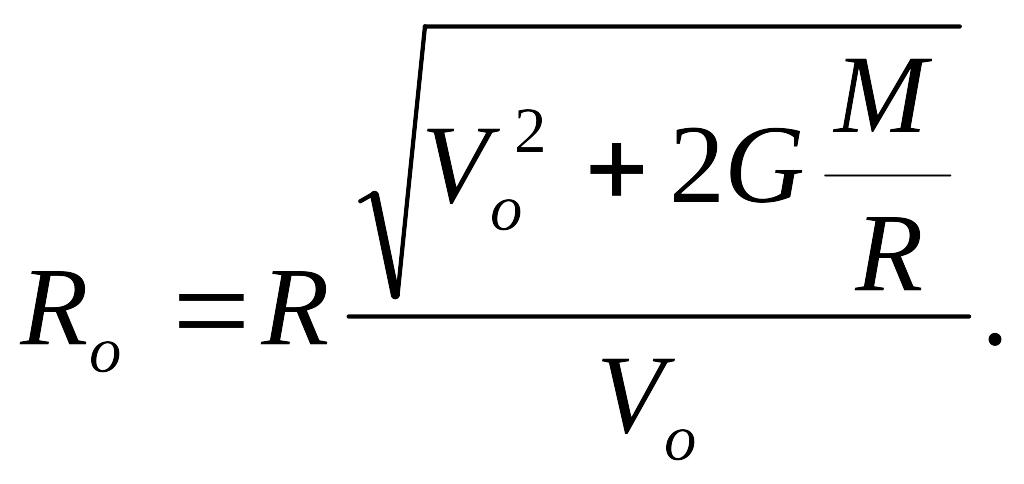
Теперь не составляет большого труда найти число метеоритов, попадающих на Землю. Оно будет равно, как отмечалось выше, числу метеоритов, находящихся внутри цилиндра радиусом Ro и длиной h,
.