Операторні алгоритми Ван Хао

Операторний алгоритм Ван Хао задається послідовністю наказів спеціального виду. Кожен наказ має певний номер і містить вказівки: яку операцію варто виконати над заданим об'єктом і наказ із яким номером варто далі виконати над результатом даної операції. Загальний вид такого наказу:

(11)

де і — номер наказу,

?-елементарна операція над об'єктом, ?, ? - номера деяких наказів. У термінах машин Т'юрінга номера наказів відповідають номерам конфігурацій машини, а елементарна операція надоб'єктом - елементарній дії над конфігурацією при деякому стані.

Виконати наказ (11) над числом х в операторному алгоритмі— значить знайти число ω(х) і далі перейти до виконання над ω (x) наказу з номером α. Якщо ж ω(х) не визначено, то перейти до виконання над числом х наказу з номером β.

Наприклад, виконавши над числом 24 наказ

одержимо число 4 і вказівка виконувати далі над 4 наказ із номером 7. Виконавши цей наказ над числом 23, одержимо знову число 23 і вказівку виконувати над 23 наказ із номером 13.

Заключному стану машини Т'юрінга в операторних алгоритмах відповідає наказ виду

який означає, що обчислення варто зупинити. Число, над яким варто виконати цей наказ, є результат обчислень.

У загальному випадку результат виконання наказу (11) над числом х будемо зображувати парою (z, у), де z — отримане число, y — номер наказу, що повинен виконуватися далі над z.

Програмою операторного алгоритму називається послідовність наказів виду:

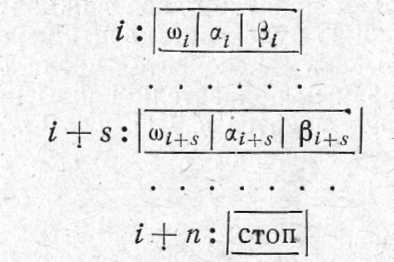
(12)

де ω_i(x), …, ω _i+s(x)—задані одномісні часткові функції, що визначають елементарні операції над об'єктом х;

α_i, β_i, ..., α_i+s, β_i+s — якісь натуральні числа з послідовності і, і + 1, ..., і + п.

Переробити х відповідно до даного операторного алгоритму — це значить виконати над х послідовність наступних дій.

і — крок. Знаходимо ω_і(х). Якщо ω_i(х) визначено, то результатом будуть пари чисел [ω_i(x), а_і]. Якщо ω (x) не визначено, то результатом і-го кроку будуть пари (х,β_i ).

і + 1 — крок, якщо результат попереднього кроку х, β_i, де β_i = і + 1. Знаходимо ω_i+1(x). Якщо вона визначена, то результатом буде пара [ω_i+1(x), α_i+1], якщо не визначена, то результатом буде пара (х, β_i+1) і т.д.

і + п — 1 — крок. Якщо як результат на даному кроці вийде пара, що вказує на заключний оператор (z, і+п), то процес обривається й число z є результатом переробки числа х відповідно до заданого алгоритму (z =ω _i+n-1(x)).

Якщо ж у процесі виконання алгоритму не виникае пара, що вказує на заключний оператор, то результатом переробки х буде «невизначене значення».

Якщо функція усюди визначена, то символ р не впливає на процес обчислень і тому звичайно опускається. У цьому випадку наказ має вигляд i:ω‌‌‌│a. Говорять, що операторний алгоритм A із програмою (х) обчислює часткову функцію f(x), якщо алгоритм А переробляє кожне натуральне число х у f(x). Зокрема, якщо f(x) не визначено, то процес переробки х згідно, програмі (12) повинен бути нескінченним.

Природа функцій, обчислюваних за допомогою операторних алгоритмів Ван-Хао, залежить від того, які функції сог входять у записи наказів. Має місце наступна теорема, що визначає природу функцій ω_i.

Теорема (3). Для того щоб часткова функція f(x) була обчислюваною за допомогою операторного алгоритму, програма якого містить лише частково рекурсивні функції ω_i (х) з рекурсивною областю визначеності, необхідно й досить, щоб f(x) була частково рекурсивною.

Необхідність умов очевидна, і ми обмежимося лише доказом їхньої достатності.

Насамперед уведемо поняття однієї важливої для доказу функції. Цю функцію будемо позначати через ех (х, у) або скорочено ех_ху й називати експонентою числа р_х у числі y. При y≠0 вважаемо ех_ху рівним показнику найвищого ступеня простого числа р_х, на яку ділиться y. Для y = 0 вважаемо по визначенню ех_х0= 0 для всіх значень х.

Наприклад,

ех₂8 = 3, ex₁8 = 0, ех₀0 = 0.

Ясно, що алгоритм із програмою

обчислює ніде не визначену функцію f(x).

Нехай частково рекурсивна функція f (х) має непустий графік. Тоді цей графік можна представити у вигляді сукупності пар <α(t), β(t)> (t = 0, 1, ...), де α і β -підходящі примітивно рекурсивні функції. Позначимо через v(x) вираження 2^x й уведемо часткову функцію С0 (х), думаючи

ω

Функция ω(х) частично рекурсивна с рекурсивной областью определенности. Легко убедиться, что операторный алгоритм, имеющий программу ,

(x)=

обчислює саме функцію f (х). Справді, виконавши над довільним числом х наказ 1, одержимо пару (2^х, 2). Якщо х≠а(0). те, виконавши над 2^х наказ 2, одержимо пару (2^x3¹, 2). Якщо х≠а(1), то, виконавши над 2^x3¹ наказ 2, одержимо пару (2^x3², 2) і т.д. Процес триває доти, доки, нарешті, вийде пара (2^x3ⁿ, 2), для якої х = а(п). Тому що ω(2^x3ⁿ) не визначено, то над числом 2^x3ⁿ тепер треба виконати наказ 3, у результаті якого одержимо пару (п, 4). Виконавши над п наказ 4, одержимо пару (β(n), 0). Тому що х = а(п), то β(n) =f(x), і, отже, алгоритм переробляє х bf(x), що й було потрібно.

Побудована програма для обчислення функцій f(x) виявилася досить тривіальної внаслідок того, що запас функцій, припустимих у наказах, був дуже великим. Природно, чим менше запас, тим важче будувати потрібні програми. Тому безсумнівний інтерес представляє наступна теорема, що ми приводимо без доказу.

Теорема Мінського (4). Для кожної частково рекурсивної функції f(x) існує операторний алгоритм, програма якого складається з наказів виду

для будь-якого х, що переробляє 2^х в 2^f(x).

Іншими словами, будь-яка частково рекурсивна функція f (х) обчислювана за допомогою підходящого алгоритму, програма якого складається з наказів наведеного виду, за умови, що значення аргументу й функції кодуються числами 2, 2^f(x).