
- •Оглавление
- •IV. Решение типовых задач 32
- •V. Варианты контрольных работ 54
- •Список литературы 84 введение
- •I. Кратные и криволинейные интегралы
- •Понятие интеграла от скалярной функции
- •2. Основные свойства интегралов
- •3. Вычисление интегралов
- •3.1. Определенный интеграл
- •3.2. Криволинейный интеграл
- •3.3. Двойной интеграл
- •3.4. Поверхностный интеграл второго рода
- •3.5. Тройной интеграл
- •II. Применение кратных и криволинейных интегралов.
- •III. Элементы теории поля
- •Понятие поля
- •Векторные линии
- •Работа силового поля. Криволинейный интеграл второго рода. Циркуляция вектора вдоль замкнутого контура
- •Поток вектора через поверхность
- •Вектор площадки
- •Понятие потока вектора через поверхность
- •Гидродинамический смысл потока вектора через поверхность. Поток жидкости через поверхность
- •Поток вектора через плоскую кривую l
- •Свойства и вычисление потока вектора через поверхность
- •Оператор Гамильтона «набла»
- •Дивергенция векторного поля
- •Ротор (вихрь) векторного поля
- •Потенциальное векторное поле
- •8.1 Плоское потенциальное поле
- •IV. Решение типовых задач
- •Вычисление и применение двойного интеграла
- •Вычисление и применение тройного интеграла
- •Вычисление и применение поверхностного интеграла первого рода
- •Вычисление и применение криволинейного интеграла.
- •V. Варианты контрольных работ Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Список литературы
8.1 Плоское потенциальное поле
Если поле плоское,
т.е.
![]()
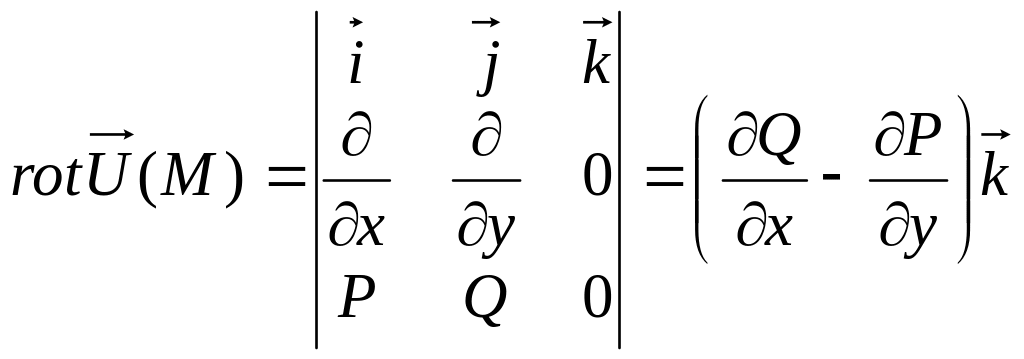 (33)
(33)
- поле называется
потенциальным при
![]() .
.
В этом случае
![]() ,
т.е.
,
т.е.
![]() и
и
![]() для всех дуг, натянутых между точками
А
и В.
для всех дуг, натянутых между точками
А
и В.
Получили, что при
криволинейный
интеграл не зависит от пути интегрирования.
Работа силы
![]() не зависит от пути, по которому движется
точка. Тогда криволинейный интеграл по
любому замкнутому контуру в заданной
области равен нулю.
не зависит от пути, по которому движется
точка. Тогда криволинейный интеграл по
любому замкнутому контуру в заданной
области равен нулю.
![]() (34)
(34)
т.е. циркуляция
поля вдоль любого замкнутого контура
равна нулю
![]() .
.
Потенциал плоского поля находят по формуле
![]() , (35)
, (35)
где М(х,у),
М0(х0,у0)
взяты произвольно. Удобнее всего за
дугу
![]() брать двузвенную ломаную линию, звенья
которой параллельны осям координат,
так как на вертикальном звене
брать двузвенную ломаную линию, звенья
которой параллельны осям координат,
так как на вертикальном звене
![]() ,
а на горизонтальном
,
а на горизонтальном
![]() .
.
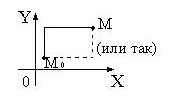
Рис. 8.1
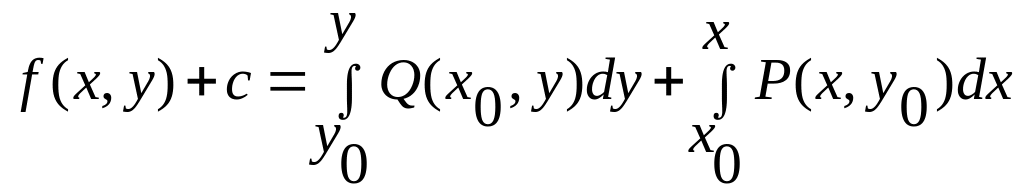 (36)
(36)
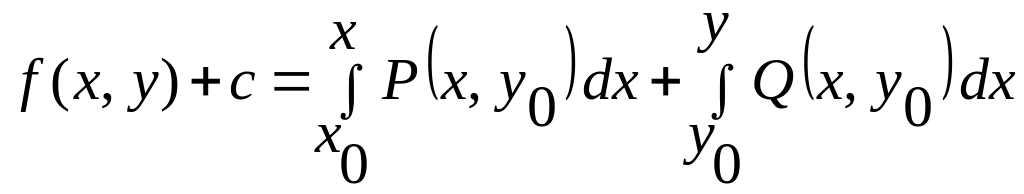
IV. Решение типовых задач
Вычисление и применение двойного интеграла
При решении этих задач используйте следующую схему:
Сделать чертеж;
Выбрать подходящие формулы (по условию задачи и по чертежу);
Найти все элементы выбранных формул;
Вычислить получившийся повторный интеграл.
Пример 1
Вычислить
![]() если D:
если D:
![]()
Изменить порядок интегрирования в полученном повторном интеграле и еще раз вычислить интеграл
Решение
Построим чертеж.
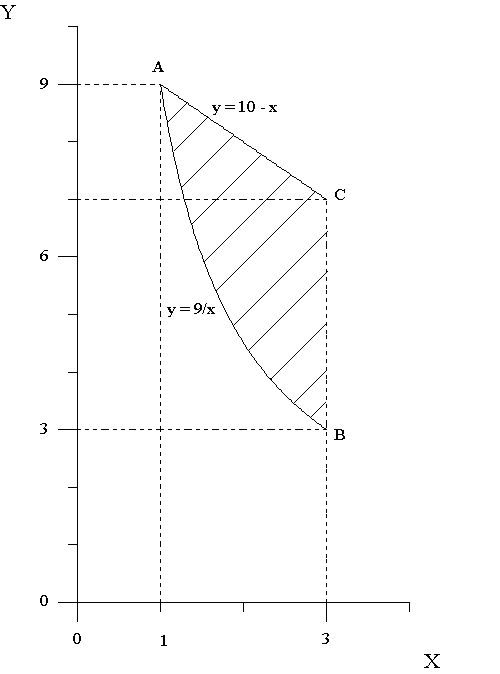
Уравнения границ
области
![]() (каждое неравенство, задающее D,
превращаем в уравнение).
(каждое неравенство, задающее D,
превращаем в уравнение).
Для вычисления выберем формулу
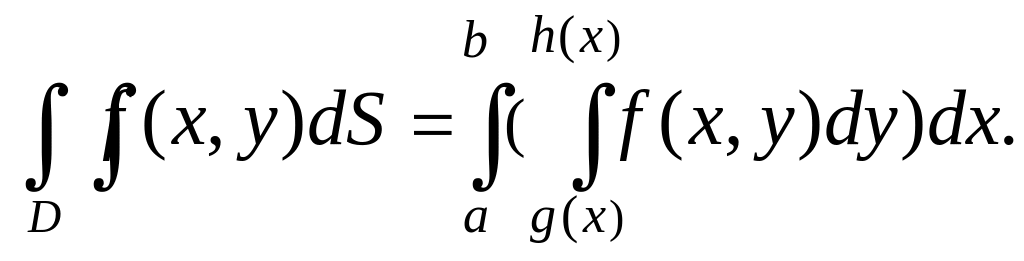
Найдем элементы формулы.
Т.к. область
расположена между прямыми x
= 1 и x
= 3, то a
= 1, b
= 3. Нижняя
граница области – дуга
![]() задана
уравнением
задана
уравнением
![]() следовательно
следовательно
![]() .
Верхняя граница – прямая AC
задана уравнением y
= 10 – x,
следовательно
.
Верхняя граница – прямая AC
задана уравнением y
= 10 – x,
следовательно
h (x) = 10 – x. Получим повторный интеграл.
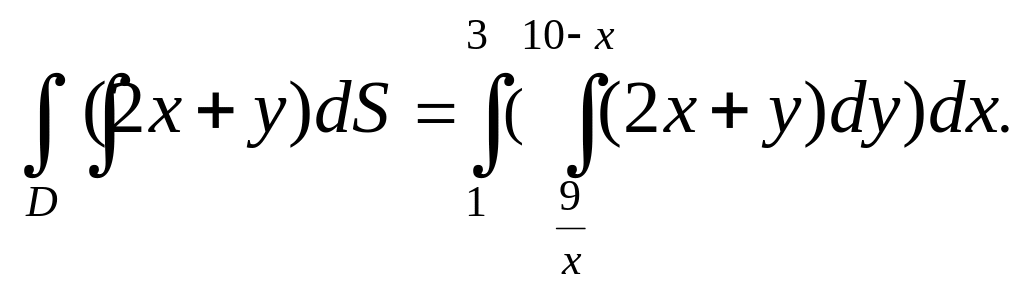
Вычислим внутренний интеграл, считая x – постоянной.
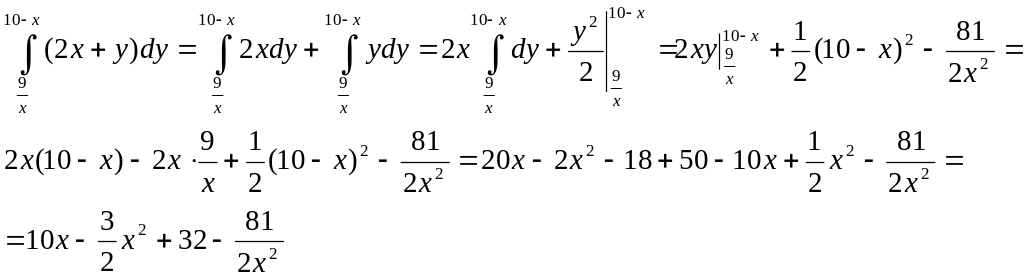
От полученной функции вычислим внешний интеграл
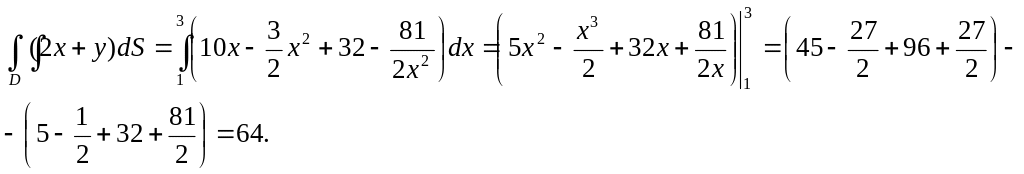
Изменить порядок интегрирования в данном случае означает, что внутренний интеграл нужно взять по x, а внешний по y и для вычисления интеграла выбрать формулу.
Выполним чертеж еще раз.
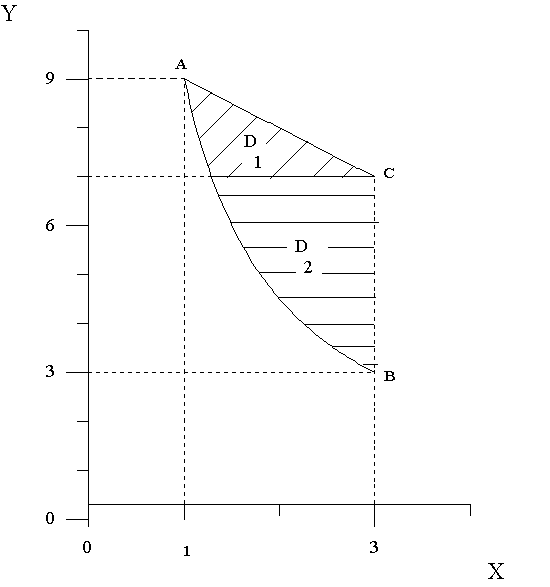
Найдем координаты точек A, B и C:
![]()
Правая граница
области D
состоит из
отрезков BC
и AC
различных прямых, следовательно область
D
нужно разбить на две части
![]() и
и
![]() , тогда
, тогда
![]() уравнения границ
нужно решить относительно x.
Левая граница обеих частей – дуга
:
уравнения границ
нужно решить относительно x.
Левая граница обеих частей – дуга
:
![]() Правая граница области
-
отрезок BC:
x
= 3. Правая
граница области
-
отрезок AC:
Правая граница области
-
отрезок BC:
x
= 3. Правая
граница области
-
отрезок AC:
![]() Область
расположена между прямыми y
= 3 и y
= 7. Внутри
области
x
изменяется от границы
Область
расположена между прямыми y
= 3 и y
= 7. Внутри
области
x
изменяется от границы
![]() до границы x
= 3. Получим
до границы x
= 3. Получим
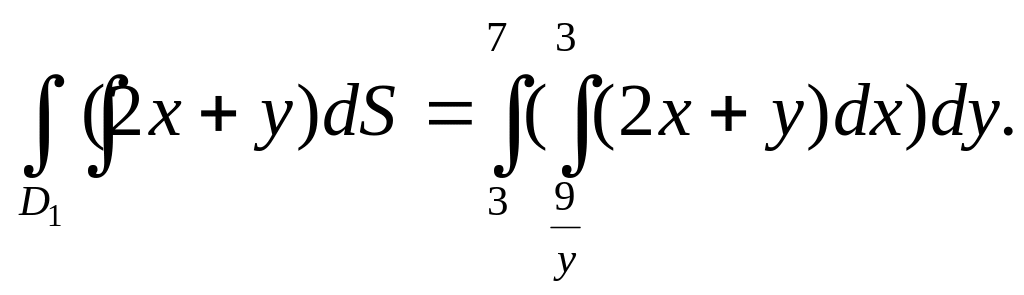 Область
расположена между прямыми y=7
и y=9.
Внутри области
x
изменяется
от границы
до границы x
= 10 – y.
Область
расположена между прямыми y=7
и y=9.
Внутри области
x
изменяется
от границы
до границы x
= 10 – y.
Получим![]()
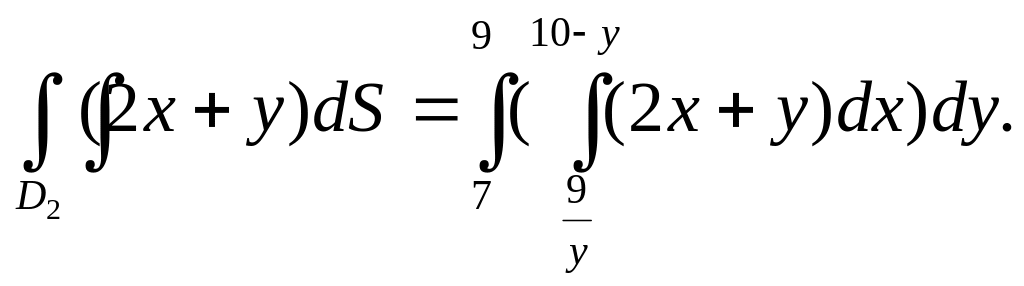
Следовательно
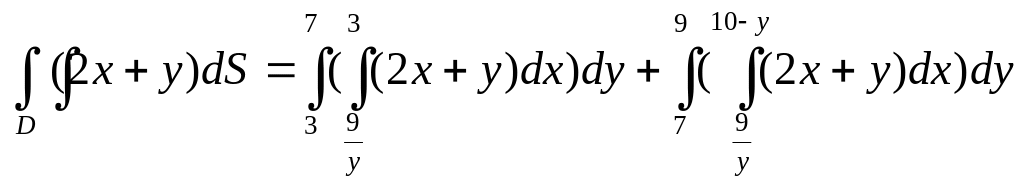 -
-
порядок интегрирования изменен.
Вычислим
Внутренний интеграл вычисляем, считая y – постоянной.
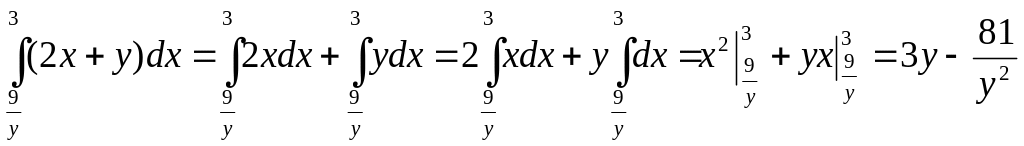 ,
,
Тогда 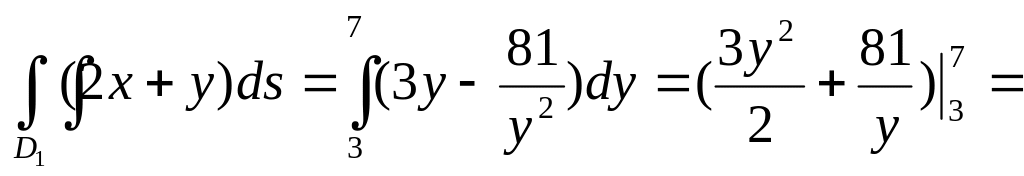
![]()
Вычислим
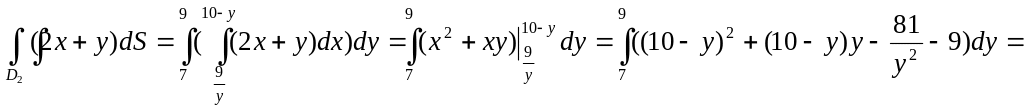
![]() .
.
Следовательно
![]()
Мы убедились, что в данном случае проще вычислить внутренний интеграл по y, а внешний по x.
Ответ:
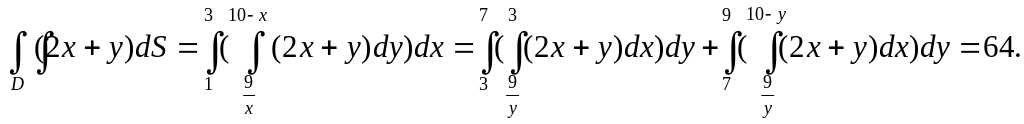
Пример 2
Найти статические
моменты относительно осей координат
однородной фигуры: ограниченной линиями
![]() =4,
2x
+ y
= 2 и
расположенной в первой четверти, если
поверхностная плотность массы
=4,
2x
+ y
= 2 и
расположенной в первой четверти, если
поверхностная плотность массы
![]() .
.
Решение
Выполним чертеж.
Л
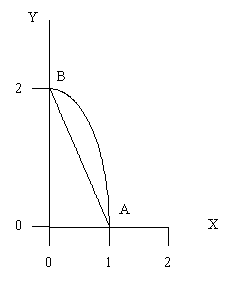
![]() - эллипс
- эллипс
![]()
2x + y = 2 – прямая.
При построении получили точки пересечения линий A (1;0), B (0;2). По условию задачи выберем формулы вычисления статических моментов плоской области.
![]() .
.
При вычислении
![]() внутренний интеграл удобнее брать по
y,
а при вычислении
внутренний интеграл удобнее брать по
y,
а при вычислении
![]() по x,
т.к. в этом случае внешние интегралы
получаются более простыми (проверьте
это). Используем обе формулы вычисления
двойного интеграла, а значит, уравнения
границ области нужно решить и относительно
y
и относительно x.
по x,
т.к. в этом случае внешние интегралы
получаются более простыми (проверьте
это). Используем обе формулы вычисления
двойного интеграла, а значит, уравнения
границ области нужно решить и относительно
y
и относительно x.
Отрезок прямой
![]() или
или
![]()
Дуга эллипса
![]() или
или
![]()
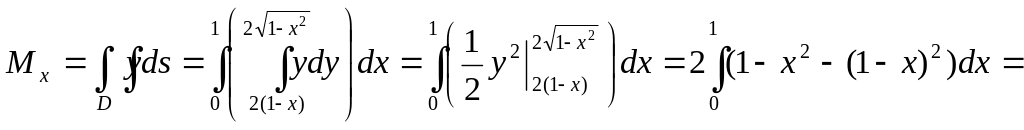
![]()
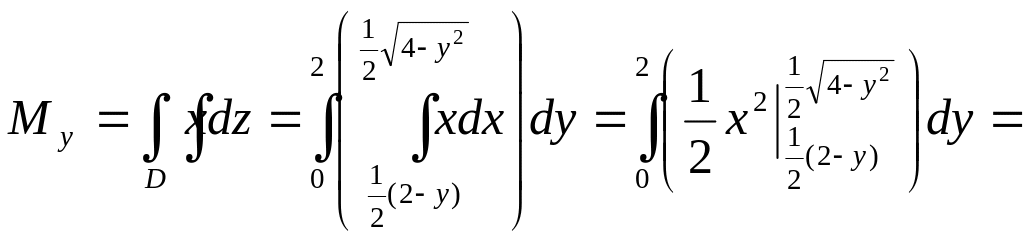
![]()
![]()
Ответ:
![]()
Пример 3
Найти момент
инерции относительно оси ox
фигуры, ограниченной линиями
![]() если поверхностная плотность массы
если поверхностная плотность массы
![]()
Решение
Выполним чертеж
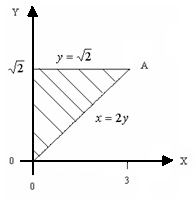
По условию задачи выберем формулу момента инерции
![]()
Область D удобна для вычисления повторного интеграла при любом порядке интегрирования. Подынтегральная функция по x интегрируется значительно легче, чем по y , поэтому возьмем внутренний интеграл по x , а внешний по y.
Решим уравнения
границ относительно x.
Левая граница:
![]() (задана). Правая граница:
(задана). Правая граница:
![]() .
.
Область D
расположена между прямыми
![]() и
и
![]() Внутри области x
изменяется
от границы
до границы
Внутри области x
изменяется
от границы
до границы
![]() значит
значит
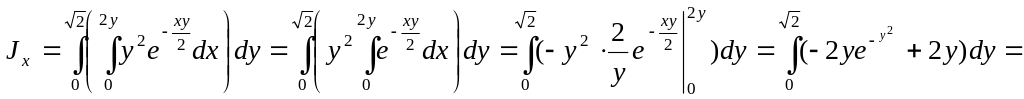
![]()
Ответ:
![]()
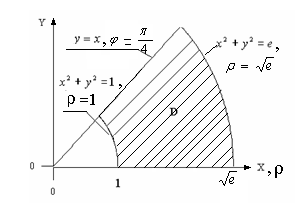
Пример 4
Вычислить
![]() если D:
если D:![]()
Решение
Построим область
D.
Границы области:
![]() -
окружности радиусов 1
и
-
окружности радиусов 1
и
![]() с центром в начале координат y
= 0, y
= x
– прямые.
с центром в начале координат y
= 0, y
= x
– прямые.
Т.к. область
интегрирования – часть кольца, перейдем
к полярным координатам. В подынтегральном
выражении заменим x,
y
и ds
по формулам
![]()
Предварительно заменим
![]()
Тогда
![]()
запишем в полярных координатах уравнения границ области
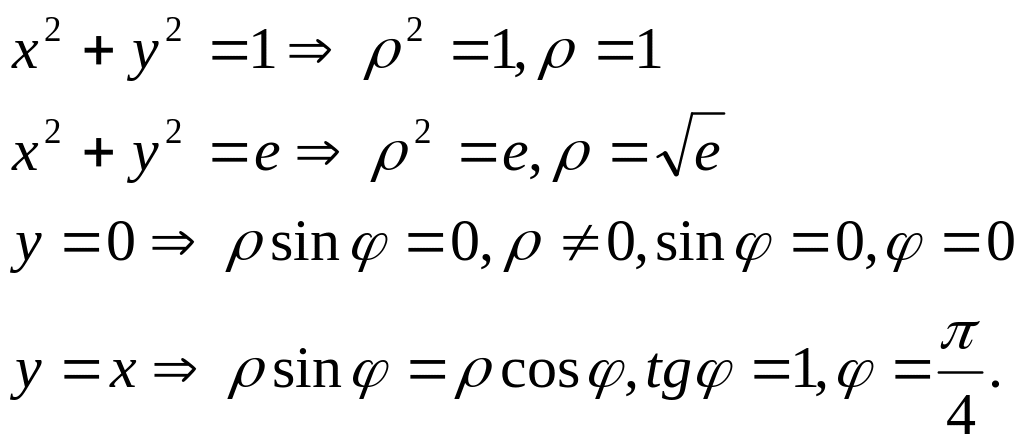
В
полярных координатах внешний интеграл
всегда берем по
![]() ,
а внутренний по
,
а внутренний по
![]() .
Область расположена в секторе между
лучами
.
Область расположена в секторе между
лучами![]() и
и
![]() .
Внутри области
изменяется
от границы
.
Внутри области
изменяется
от границы
![]() до границы
до границы
![]() .Следовательно,
по формуле
.Следовательно,
по формуле
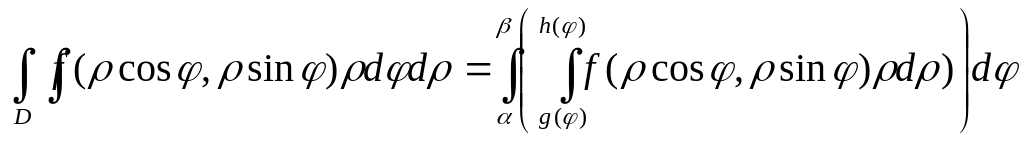
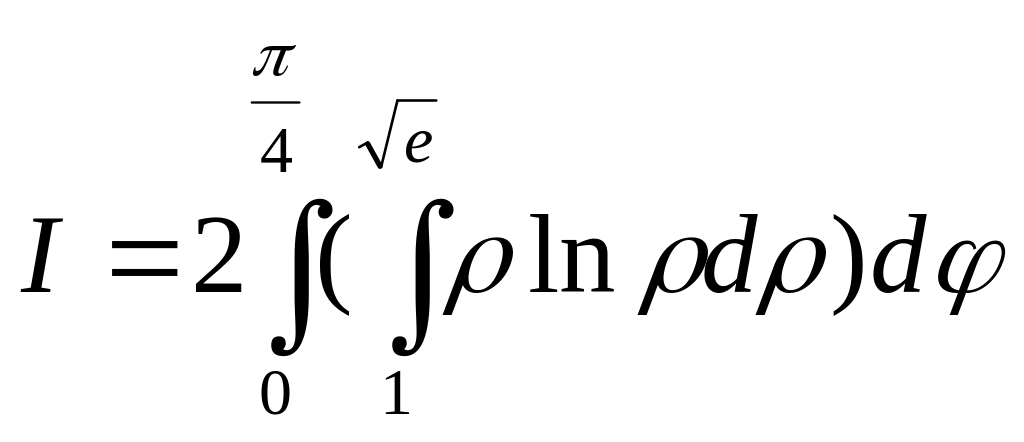 .
.
Внутренний интеграл вычислим, используя формулу интегрирования по частям:
![]()
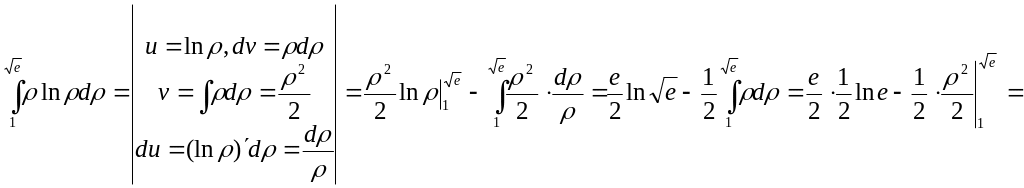
![]()
Тогда
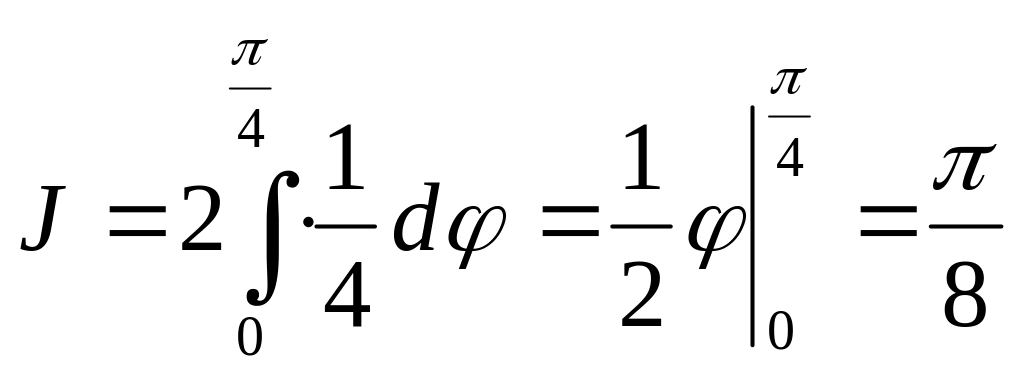
Ответ:
![]()
Пример 5
Вычислить площадь
общей части двух кругов:
![]()
Решение
Сделаем чертеж
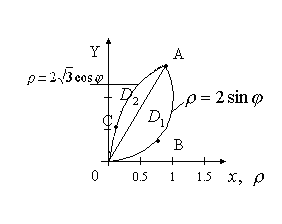
![]() - окружность
- окружность
![]() с центром в точке
с центром в точке
![]() радиуса
радиуса
![]()
![]() - окружность
- окружность
![]() с центром в точке
с центром в точке
![]() радиуса
радиуса
![]()
Выберем формулу площади фигуры в полярных координатах, т.к. область ограничена окружностями
![]()
Граница области
состоит из дуг
![]() и
и
![]() разных окружностей, разобьем область
D
лучом OA
на две части
разных окружностей, разобьем область
D
лучом OA
на две части
![]()
![]() и
и
![]() .
.
Площадь
![]() обозначим
обозначим
![]() площадь
площадь
![]() обозначим
обозначим
![]()
Уравнения окружностей запишем в полярных координатах
![]()
![]() .
.
Найдем уравнение луча OA, для чего найдем полярный угол точки A пересечения окружностей.
![]()
![]()
Уравнение луча
OA:![]()
Т.к. окружность
касается оси ox,
то область
ограничена лучом
.
Т.к. окружность
касается оси oy,
то область
ограничена лучом
![]() .
.
Область
расположена в секторе между лучами
и
,
внутри области
изменяется от
![]() до
до
![]() .
Запишем
.
Запишем
![]() и вычислим интеграл по формуле
и вычислим интеграл по формуле
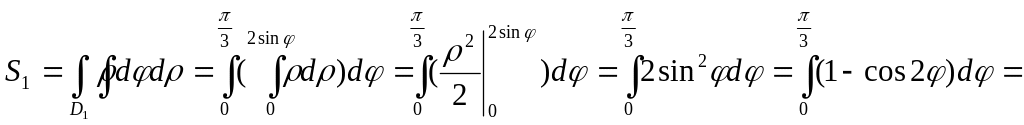
=![]()
Область
расположена в секторе между лучами
и
,
внутри области
изменяется от
до
![]() .
.
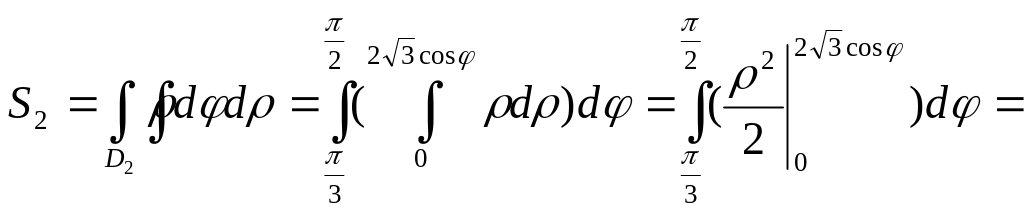
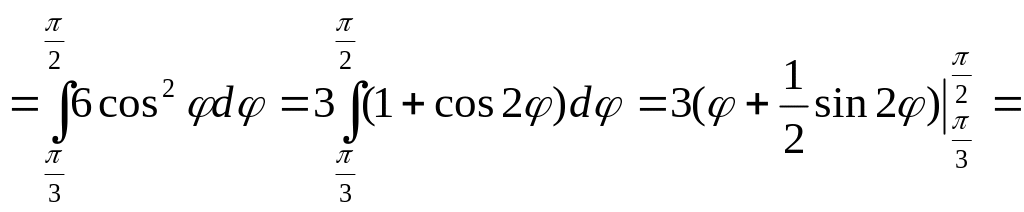
![]() .
.
Следовательно
![]()
Ответ:
![]() .
.
