
- •Оглавление
- •IV. Решение типовых задач 32
- •V. Варианты контрольных работ 54
- •Список литературы 84 введение
- •I. Кратные и криволинейные интегралы
- •Понятие интеграла от скалярной функции
- •2. Основные свойства интегралов
- •3. Вычисление интегралов
- •3.1. Определенный интеграл
- •3.2. Криволинейный интеграл
- •3.3. Двойной интеграл
- •3.4. Поверхностный интеграл второго рода
- •3.5. Тройной интеграл
- •II. Применение кратных и криволинейных интегралов.
- •III. Элементы теории поля
- •Понятие поля
- •Векторные линии
- •Работа силового поля. Криволинейный интеграл второго рода. Циркуляция вектора вдоль замкнутого контура
- •Поток вектора через поверхность
- •Вектор площадки
- •Понятие потока вектора через поверхность
- •Гидродинамический смысл потока вектора через поверхность. Поток жидкости через поверхность
- •Поток вектора через плоскую кривую l
- •Свойства и вычисление потока вектора через поверхность
- •Оператор Гамильтона «набла»
- •Дивергенция векторного поля
- •Ротор (вихрь) векторного поля
- •Потенциальное векторное поле
- •8.1 Плоское потенциальное поле
- •IV. Решение типовых задач
- •Вычисление и применение двойного интеграла
- •Вычисление и применение тройного интеграла
- •Вычисление и применение поверхностного интеграла первого рода
- •Вычисление и применение криволинейного интеграла.
- •V. Варианты контрольных работ Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Список литературы
Дивергенция векторного поля
Пусть в трехмерном
пространстве (или в области G)
определено векторное поле
.
Возьмем произвольную точку М
и окружим замкнутой поверхностью σ.
Вычислим поток
![]() векторного поля через поверхность σ.
Найдем объем v
области, ограниченной σ.
Дивергенцией (расходимостью)
векторного поля через поверхность σ.
Найдем объем v
области, ограниченной σ.
Дивергенцией (расходимостью)
![]() векторного поля
в точке М
называется предел отношения потока
векторного поля через замкнутую
поверхность σ
к объему области, ограниченной σ,
вычисленный при условии, что поверхность
σ
стягивается в точку М.
векторного поля
в точке М
называется предел отношения потока
векторного поля через замкнутую
поверхность σ
к объему области, ограниченной σ,
вычисленный при условии, что поверхность
σ
стягивается в точку М.
![]() . (26)
. (26)
Если в пространстве введена прямоугольная система координат Охуz и
![]() ,
то
,
то
![]()
пишут ![]() . (27)
. (27)
Ранее мы говорили, что все эти частные производные существуют. Используя гидродинамическую интерпретацию, считаем поле стационарным полем скоростей несжимаемой текущей жидкости. Это течение может быть обусловлено наличием источников – точек, производящих жидкость, и стоков – точек, поглощающих жидкость. Величина дает объем жидкости, протекающей в единицу времени с внутренней стороны σ на внешнюю. Но эта величина равна количеству жидкости, вырабатываемой всеми источниками, находящимися в области, ограниченной σ, т.е. равна суммарной мощности всех источников внутри σ. Тогда предел отношения мощности источников в области к объему области, найденный при условии, что область стягивается (сжимается) в точку М, равен плотности мощности источников жидкости в этой точке.
Итак, в гидродинамической интерпретации дивергенция векторного поля в точке М – это плотность мощности источников жидкости в этой точке.
Есть и другие интерпретации. Так, в электрическом векторном поле напряженности, созданном электрическими зарядами, распределенными в пространстве, дивергенция вектора напряженности является плотностью распределения электрических зарядов в данной точке поля.
Ротор (вихрь) векторного поля
Пусть в пространстве (или в области G) определена прямоугольная система координат и задано векторное поле
![]() .
.
Ротором
![]() поля
в точке М
называют вектор
поля
в точке М
называют вектор
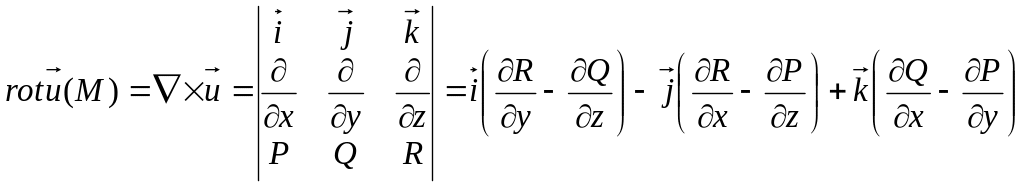 (28)
(28)
Этот вектор характеризует завихренность поля в точке М (тенденцию к вращению). Проведем через точку М плоскость Г, ее ориентацию в пространстве зададим единичным нормальным вектором , в точке М.
В плоскости Г возьмем замкнутую кривую L, обходящую точку М, и выберем направление обхода L таким, чтобы с конца обход казался происходящим против движения часовой стрелки.
Обозначим площадь,
ограниченную контуром L,
через ΔS.
Найдем циркуляцию векторного поля
вдоль контура L
![]() .
.
Доказывается, что
проекция ротора поля
в точке М
на вектор
равна пределу отношения циркуляции
поля по контуру L
к площади ΔS,
ограниченной контуром, при условии, что
контур L
стягивается в точку М,
а
![]() .
.
![]() (29)
(29)
Потенциальное векторное поле
Векторное поле , заданное в односвязной области G, называется потенциальным, если существует такая скалярная функция f(M), что во всех точках вектор
![]() (30)
(30)
В этом случае функция f(M)=f(x,y,z) называется потенциалом векторного поля . (Для силовых полей f(M) называется силовой функцией, потенциалом называется (-1)f(M)=-f(M).
Теорема (признак потенциального поля)
Для того, чтобы
векторное поле
было потенциальным в односвязной области
G,
необходимо и достаточно, чтобы в каждой
точке М этой
области
![]() .
.
Необходимость
можно формально рассмотреть:
![]() .
«Векторы»
и
f
коллинеарны,
следовательно, их векторное произведение
равно нулю
.
«Векторы»
и
f
коллинеарны,
следовательно, их векторное произведение
равно нулю
![]() (31)
(31)
Пусть
![]() .
.
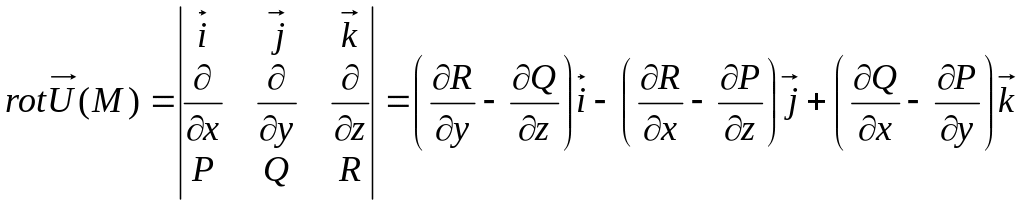 .
.
Получим, что поле является потенциальным в том и только в том случае, когда
![]() (32)
(32)
