4. Поток вектора через поверхность

1. Вектор площадки

Двусторонняя поверхность в пространстве называется ориентированной, если указано, какая ее сторона считается наружной, а какая внутренней. Можно рассматривать разные способы ориентации, например

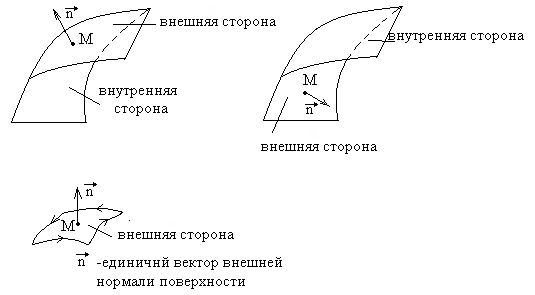
Рис. 4.1

Часто при рассмотрении элементарной части содержащей точку М ориентированной поверхности важна только площадь этой части, а ее форма (круг, прямоугольник и т. д.) не играет никакой роли. Тогда эту часть поверхности изображают нормальным вектором поверхности, направленным от внутренней стороны поверхности к внешней, модуль, которого равен площади этой элементарной части поверхности.

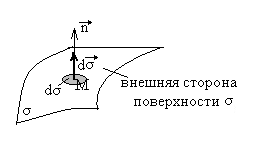
Рис. 4.2

Такой вектор называют вектором площадки (или векторной площадью площадки) в точке М. Если площадь выбранной площадки равна dσ, то вектор обозначают . Если найден единичный вектор внешней нормали поверхности , то вектор площадки

. (21)

В частности, вектор кривой в точке М направлен по нормали к кривой в выбранную сторону, причем модуль вектора равен дифференциалу длины дуги кривой . Так как вектор направлен по касательной к кривой в точке М(х,у) и модуль , то вектор кривой можно взять равным или , потому что в этом случае скалярное произведение ,значит , т.е. направлен по нормали к кривой L и .

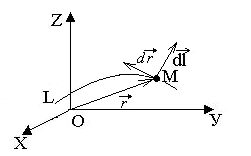
Рис. 4.3

2. Понятие потока вектора через поверхность

Пусть в области G задано векторное поле и ориентированная гладкая поверхность σ. Потоком векторного поля через поверхность σ называют скалярную величину, равную поверхностному интегралу

. (22)

Где - единичный вектор внешней нормали; - вектор элементарной площадки поверхности σ.

Если ориентацию поверхности изменить на противоположную, то поток изменит только знак.

Часто поток рассматривают как «количество векторных линий», пересекающих поверхность изнутри наружу. «Количество» (в кавычках, т. к. число не целое) понимают в алгебраическом смысле, т.е., если одна часть σ пересекается векторными линиями изнутри наружу, а другая часть – снаружи внутрь, то «количество» может быть положительным, отрицательным или равным нулю.

3. Гидродинамический смысл потока вектора через поверхность. Поток жидкости через поверхность

Рассмотрим стационарное течение несжимаемой жидкости (или газа) в области G. В любой точке скорость частицы жидкости имеет определённое значение , т.е. в области G имеем векторное поле скоростей. Поместим в область G гладкую ориентированную поверхность σ и найдем объем жидкости, протекающей через поверхность σ за единицу времени изнутри наружу. Возьмем на поверхности σ элемент dσ, содержащий точку М и найдем элемент объема жидкости, протекающей через dσ изнутри наружу за единицу времени. Он равен объему косого цилиндра с основанием dσ и образующей .

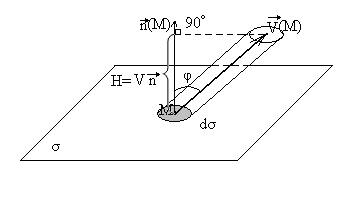
Рис. 4.4

Высота цилиндра равна проекции вектора скорости на единичный вектор внешней нормали , т.е. равна – скалярному произведению векторов.

Тогда объем цилиндра равен , т.е. элементарный объем жидкости равен скалярному произведению вектора скорости на вектор площадки . Суммарные элементарные объемы жидкости для всех элементов поверхности , получим, что за единицу времени через всю поверхность изнутри наружу проходит объем жидкости, равный поверхностному интегралу

т. е. равный потоку вектора через поверхность .