Вариант 30
1.
Найти моменты инерции относительно
осей координат фигуры, ограниченной
линиями
если поверхностная плотность массы в
каждой точке фигуры равна ординате
точки.
Ответ:
2.
Найти объем цилиндрического тела,
ограниченного плоскостями
и цилиндрической поверхностью
Ответ:
3.
Найти электрический заряд, распределенный
по кривой
с линейной плотностью
Ответ:
4.
Найти работу поля
при движении точки (m
= 1) по параболе
от 0 (0,0) до А
(1,2). Найти циркуляцию вектора
по замкнутому контуру OACO,
состоящему из дуги
параболы и прямых AC
и CO,
где С
(1,
-1). Найти поток вектора
через дугу
.
Ответ:
5.
Найти центр массы однородного тела,
ограниченного поверхностями
,
z=
0.
Ответ:
6.
Найти площадь части гиперболического
параболоида az
= xy,
вырезанной цилиндром
Ответ:
Найти дивергенцию и ротор векторного поля
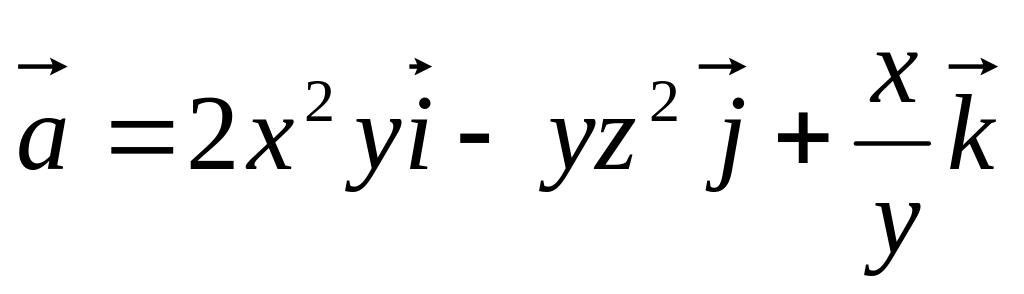в произвольной точке и в точке
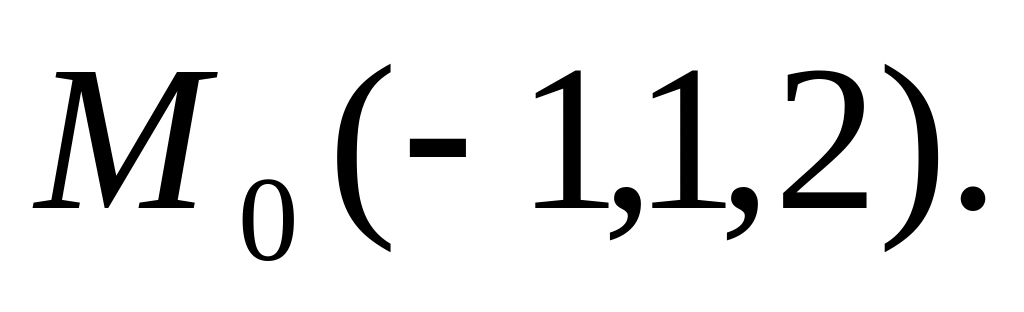
Ответ:
Список литературы
Кудрявцев Л.Д. Курс математического анализа, т.1,2,3.-М.: Высшая школа, 1988.
Исрапилов Р.Б., Баутин С.П. Курс математики, часть 3, Математический анализ функций нескольких переменных.- Екатеринбург, УГГГА, 1996.
Зельдович Я.Б., Мышкис А.Д. Элементы прикладной математики. - М.: Наука, 1965.
Кальницкий Л.А., Добротин Д.А., Жевержеев В.Ф. Специальный курс высшей математики, прикладные вопросы анализа. – М.: Высшая школа, 1976.
Берман Г.Н. Сборник задач по курсу математического анализа. – М.: Наука, 1969.
Давыдов Н.А.,Коровкин П.П., Никольский В.Н. Сборник задач по математическому анализу. – М.: Просвещение, 1964.