
- •Оглавление
- •IV. Решение типовых задач 32
- •V. Варианты контрольных работ 54
- •Список литературы 84 введение
- •I. Кратные и криволинейные интегралы
- •Понятие интеграла от скалярной функции
- •2. Основные свойства интегралов
- •3. Вычисление интегралов
- •3.1. Определенный интеграл
- •3.2. Криволинейный интеграл
- •3.3. Двойной интеграл
- •3.4. Поверхностный интеграл второго рода
- •3.5. Тройной интеграл
- •II. Применение кратных и криволинейных интегралов.
- •III. Элементы теории поля
- •Понятие поля
- •Векторные линии
- •Работа силового поля. Криволинейный интеграл второго рода. Циркуляция вектора вдоль замкнутого контура
- •Поток вектора через поверхность
- •Вектор площадки
- •Понятие потока вектора через поверхность
- •Гидродинамический смысл потока вектора через поверхность. Поток жидкости через поверхность
- •Поток вектора через плоскую кривую l
- •Свойства и вычисление потока вектора через поверхность
- •Оператор Гамильтона «набла»
- •Дивергенция векторного поля
- •Ротор (вихрь) векторного поля
- •Потенциальное векторное поле
- •8.1 Плоское потенциальное поле
- •IV. Решение типовых задач
- •Вычисление и применение двойного интеграла
- •Вычисление и применение тройного интеграла
- •Вычисление и применение поверхностного интеграла первого рода
- •Вычисление и применение криволинейного интеграла.
- •V. Варианты контрольных работ Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Список литературы
Вариант 14
1. Найти момент инерции относительно оси oy однородного треугольника с вершинами A (,1); B (1,2); С (3,3), если поверхностная плотность массы
Ответ:
![]()
2.
Найти статический момент относительно
оси ox
однородной фигуры
![]() если поверхностная плотность массы
если поверхностная плотность массы
Ответ:
![]()
3.
Найти длину дуги кривой
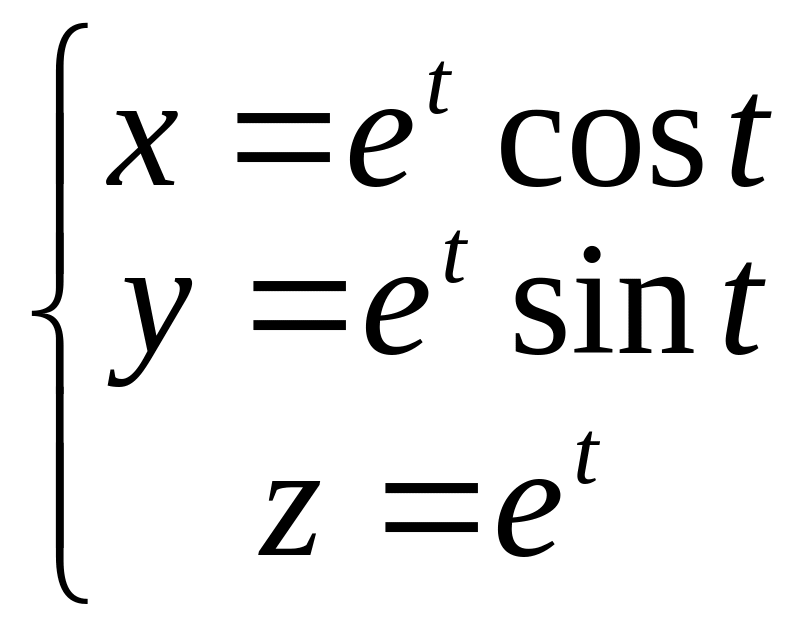 при
при
![]()
Ответ:
![]()
4.
Найти работу поля
![]() при перемещении точки по дуге гиперболы
от A
(-2,-1) до B
(-1,-2). Найти циркуляцию вектора
по
замкнутому контуру ABCA,
состоящему из дуги гиперболы
и прямых BC
и CA,
если C
(1;-1).
Найти поток вектора через дугу
при перемещении точки по дуге гиперболы
от A
(-2,-1) до B
(-1,-2). Найти циркуляцию вектора
по
замкнутому контуру ABCA,
состоящему из дуги гиперболы
и прямых BC
и CA,
если C
(1;-1).
Найти поток вектора через дугу
![]()
Ответ:
![]()
5.
Вычислить массу тела, ограниченного
поверхностями
![]() z
= 2, если плотность массы
z
= 2, если плотность массы
![]()
Ответ:
![]()
6.
Найти электрический заряд части
поверхности конуса
![]() вырезанной цилиндром
вырезанной цилиндром
![]() если поверхностная плотность заряда
если поверхностная плотность заряда
![]()
Ответ:
![]()
7.
Найти дивергенцию и ротор векторного
поля
![]() в
точке
в
точке
M (x, y, z) и в точке (1,1,1).
Ответ:
![]()
Вариант 15
Найти координаты центра массы однородной фигуры, ограниченной линиями
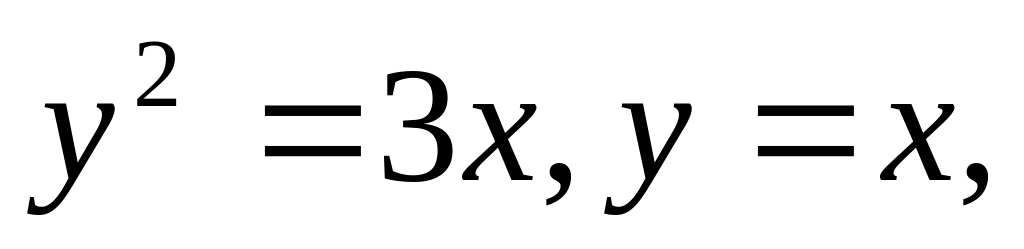 если поверхностная плотность массы
если поверхностная плотность массы
Ответ:
![]()
Найти момент инерции относительно начала координат однородной фигуры, ограниченной кривой
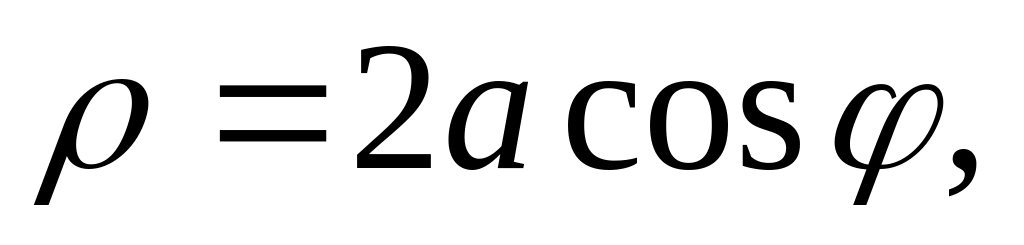 если плотность массы
если плотность массы
Ответ:
![]()
Найти массу участка кривой
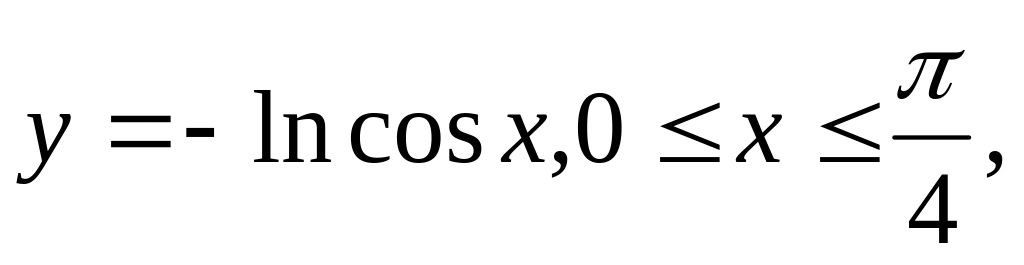 если
линейная плотность массы
если
линейная плотность массы
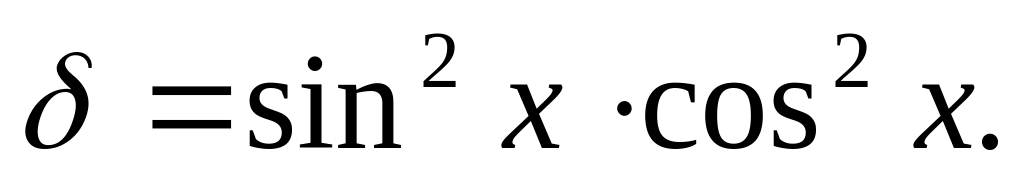
Ответ:
![]()
Найти работу поля
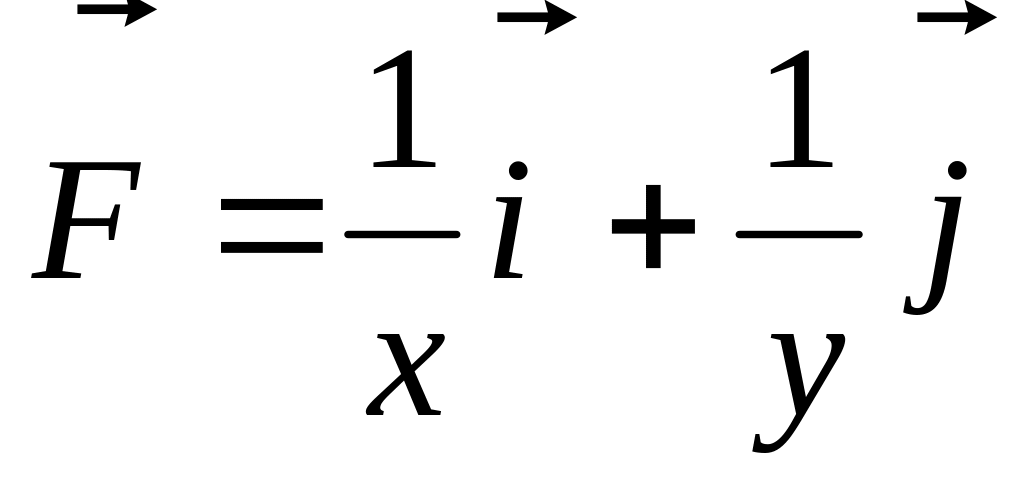 при перемещении точки по дуге окружности
при перемещении точки по дуге окружности
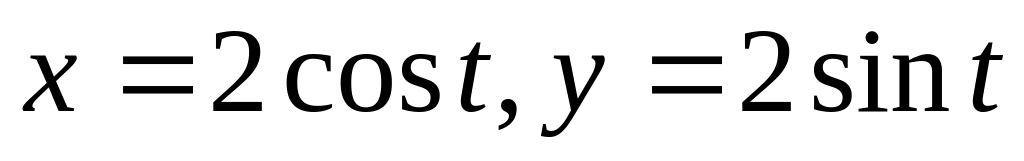 от
от
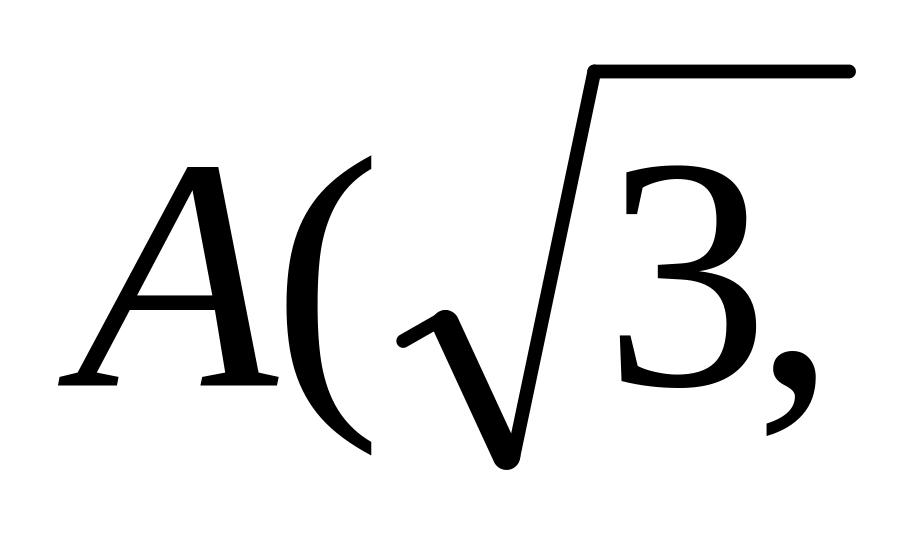 1)
до
1)
до
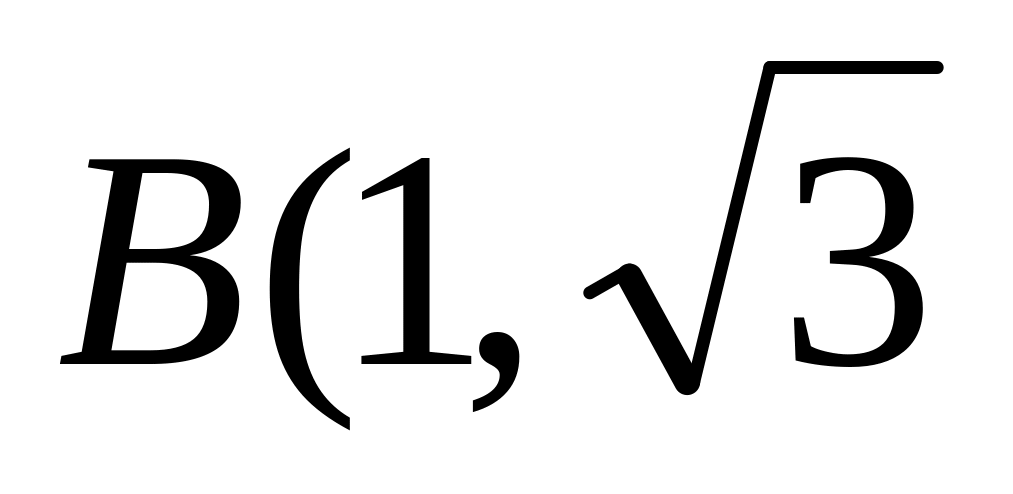 ).
Найти циркуляцию вектора
по
замкнутому контуру ACBA,
состоящему из дуги
окружности и прямых AC
и CB,
где
).
Найти циркуляцию вектора
по
замкнутому контуру ACBA,
состоящему из дуги
окружности и прямых AC
и CB,
где
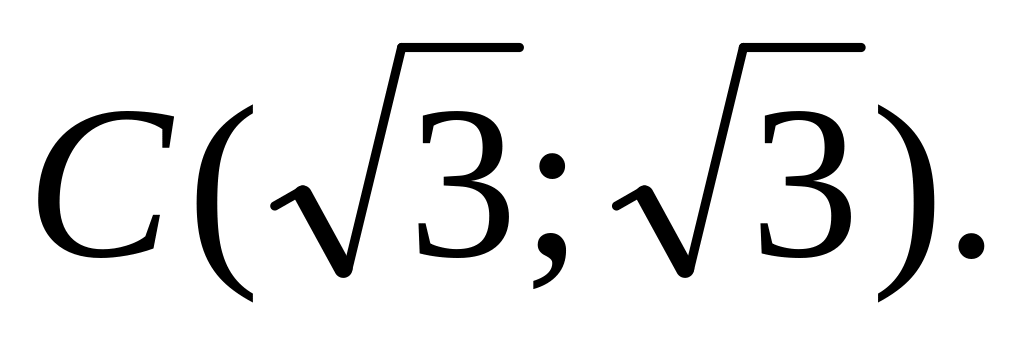 Найти поток вектора
через
дугу
окружности.
Найти поток вектора
через
дугу
окружности.
Ответ:
![]()
Найти заряд тела, ограниченного плоскостями
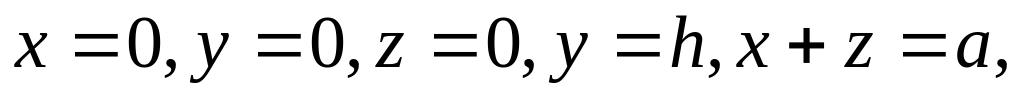 если плотность заряда
если плотность заряда
Ответ:
![]()
6.
Вычислить массу участка поверхности
![]() отсеченного плоскостью
отсеченного плоскостью
![]() если поверхностная плотность массы
если поверхностная плотность массы
![]()
Ответ:
![]()
7.Найти
дивергенцию и ротор векторного поля
![]() в произвольной точке
и в точке
в произвольной точке
и в точке
![]()
Ответ:
![]()
Вариант 16
1.
Найти координаты центра массы фигуры,
ограниченной линиями
![]() x
= y,
если поверхностная плотность массы
x
= y,
если поверхностная плотность массы
Ответ:
![]()
2. Найти массу круга радиуса R, плотность массы которого в каждой точке равна расстоянию от этой точки до окружности.
Ответ:
![]()
3.
Найти статический момент кривой
![]() относительно оси ox,
если линейная плотность массы
относительно оси ox,
если линейная плотность массы
![]()
Ответ:
![]()
4.
Найти работу поля
![]() при перемещении точки по дуге гиперболы
при перемещении точки по дуге гиперболы
![]() от A
(1;-2) до B
(2;-1). Найти циркуляцию вектора
по замкнутому контуру ACBA,
состоящему из дуги гиперболы
и прямых AC
и CB,
где
от A
(1;-2) до B
(2;-1). Найти циркуляцию вектора
по замкнутому контуру ACBA,
состоящему из дуги гиперболы
и прямых AC
и CB,
где
![]() Найти поток вектора
через дугу
гиперболы.
Найти поток вектора
через дугу
гиперболы.
Ответ:
![]()
5.
Найти электрический заряд тела,
ограниченного поверхностями
![]() z=
0,
z
= 3,
если плотность заряда
z=
0,
z
= 3,
если плотность заряда
![]()
Ответ: q = -8.
6. Найти момент инерции относительно оси oz однородной полусферы если поверхностная плотность массы
Ответ:
![]()
7.
Найти дивергенцию и ротор векторного
поля
![]() в точке M
(x,
y,
z)
и в точке
в точке M
(x,
y,
z)
и в точке
![]()
Ответ:
![]()
Вариант 17
1.
Найти момент инерции относительно оси
ox
плоской однородной фигуры, ограниченной
кривыми
![]() x
+ y
= 3, y
= 0,
если поверхностная плотность массы
x
+ y
= 3, y
= 0,
если поверхностная плотность массы
Ответ:
![]()
2.
Найти массу фигуры
![]() если поверхностная плотность массы
если поверхностная плотность массы
![]()
Ответ:
![]()
3.
Найти координаты центра массы однородной
полуокружности
![]()
Ответ:
![]()
4.
Найти работу поля
![]() при перемещении точки по дуге окружности
при перемещении точки по дуге окружности
![]() от
от
![]() до
до
![]() Найти циркуляцию вектора
по
замкнутому контуру ACBA,
состоящему из дуги
окружности и прямых AC
и CB,
если C(3,3).
Найти поток вектора
через
дугу
окружности.
Найти циркуляцию вектора
по
замкнутому контуру ACBA,
состоящему из дуги
окружности и прямых AC
и CB,
если C(3,3).
Найти поток вектора
через
дугу
окружности.
Ответ:
![]()
5.
Найти статический момент относительно
плоскости yoz
тела, ограниченного поверхностями
![]() если плотность массы
если плотность массы
Ответ:
![]()
6.
Найти электрический заряд части
поверхности
![]() отсеченной плоскостью
если плотность заряда
отсеченной плоскостью
если плотность заряда
![]()
Ответ:
![]()
7.
Найти дивергенцию и ротор поля
![]() в точке
в точке
![]() и в точке
и в точке
![]()
Ответ:
![]()
