Вариант 6
1. Найти электрический
заряд фигуры, ограниченной линиями
если поверхностная плотность заряда
Ответ:
2. Найти массу
фигуры
если поверхностная плотность массы
.
Ответ: m = 2ln2.
3. Найти момент
инерции линии
относительно оси ox,
если линейная плотность массы
Ответ:
4. Найти работу
поля
при перемещении точки по дуге эллипса
x
= 4cos
t,
y
= 3sin
t
от B
(0,3) до C
(-4,0). Найти
циркуляцию вектора
по замкнутому контуру, составленному
из дуги эллипса
и прямых CD
и DB,
если D
(0;-2). Найти поток вектора
через
дугу
эллипса.
Ответ:
5. Найти координаты
центра массы однородного тела,
ограниченного поверхностями
Ответ: С (1,0,0).
6. Найти площадь
части плоскости z
= 4 – x,
вырезанной поверхностями z
= 0, x=
.
Ответ:
.
7. Найти дивергенцию
и ротор векторного поля
в точке M
(x,
y,
z)
и в точке
Ответ: .
Вариант 7
1.
Найти абсциссу центра массы однородной
фигуры
Ответ:
2.
Вычислить площадь фигуры, ограниченной
кардиоидой
и прямой
и расположенной справа от прямой.
Ответ:
3.
Найти координаты центра массы однородной
кривой
Ответ:
4.
Найти работу поля
при перемещении точки по дуге параболы
от O
(0,0) до B
(1,2). Найти циркуляцию вектора
по замкнутому контуру OCBO
состоящему из дуги BO
параболы и прямых OC
и CB,
если C
(1;
-1). Найти поток вектора
через дугу
параболы.
Ответ:
5.
Вычислить электрический заряд тела,
ограниченного поверхностями
и расположенного в первом октанте
если плотность заряда
Ответ:
6.
Найти массу части плоскости
вырезанной цилиндром
если поверхностная плотность массы
Ответ:
7.
Найти дивергенцию и ротор векторного
поля
в точке
Ответ:
Вариант 8
1. Найти ординату центра массы однородной фигуры
Ответ:
2.
Найти момент инерции однородной фигуры
относительно оси ox,
если поверхностная плотность массы
Ответ:
3.
Найти длину дуги астроиды
Ответ:
4.
Найти работу поля
при перемещении точки по дуге параболы
от B
(-1,0)
до
O
(0,0).
Найти циркуляцию вектора
по замкнутому контуру OCBO,
состоящему из дуги BO
параболы и прямых OC
и CB,
где
C
(-1,2). Найти поток вектора
через дугу
.
Ответ:
5. Вычислить электрический заряд тела, ограниченного плоскостями x + y + z = 2, x= 0, z = 0, x – y = 0, если плотность заряда
Ответ:
6.
Найти массу полусферы
если поверхностная плотность массы
Ответ:
7.
Найти дивергенцию и ротор векторного
поля
в точке M(x,y,z)
и в точке
Ответ:
Вариант 9
1.
Найти координаты центра массы однородной
фигуры, ограниченной линиями
Ответ:
2.
Найти электрический заряд кольца
если поверхностная плотность заряда
.
Ответ:
3.
Найти электрический заряд участка
кривой
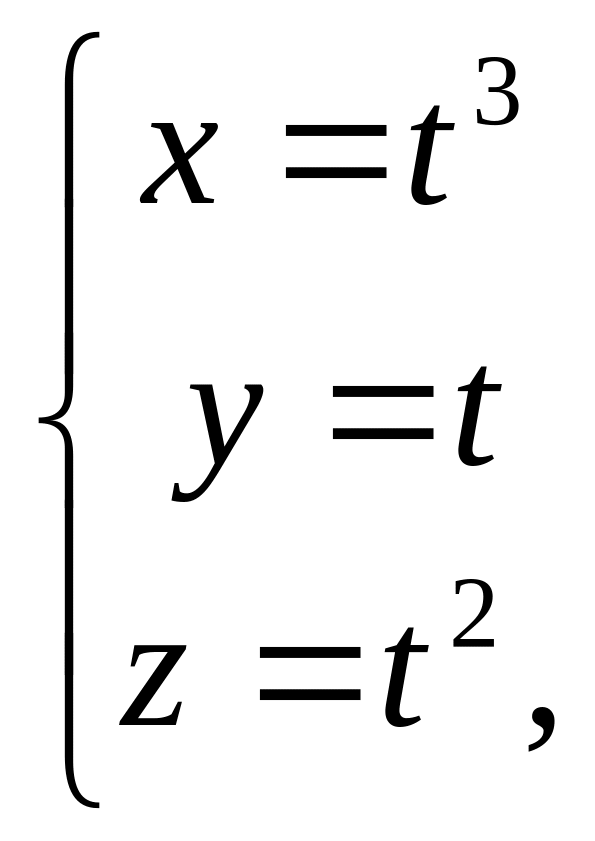
если линейная плотность заряда
.
Ответ:
4.
Найти работу поля
при перемещении точки по дуге параболы
от O
(0,0) до B
(2,0).
Найти циркуляцию вектора
по
замкнутому контуру, состоящему из дуги
и
прямых OC
и CB,
если C
(2;-1). Найти поток вектора
через дугу
Ответ:
5.
Найти массу тела, ограниченного
поверхностями
если плотность массы
Ответ:
6.
Найти момент инерции относительно оси
Oz
части однородной поверхности сферы
если поверхностная плотность массы
Ответ:
7.
Найти дивергенцию и ротор векторного
поля
в точке
и в точке
Ответ:
