
- •Оглавление
- •IV. Решение типовых задач 32
- •V. Варианты контрольных работ 54
- •Список литературы 84 введение
- •I. Кратные и криволинейные интегралы
- •Понятие интеграла от скалярной функции
- •2. Основные свойства интегралов
- •3. Вычисление интегралов
- •3.1. Определенный интеграл
- •3.2. Криволинейный интеграл
- •3.3. Двойной интеграл
- •3.4. Поверхностный интеграл второго рода
- •3.5. Тройной интеграл
- •II. Применение кратных и криволинейных интегралов.
- •III. Элементы теории поля
- •Понятие поля
- •Векторные линии
- •Работа силового поля. Криволинейный интеграл второго рода. Циркуляция вектора вдоль замкнутого контура
- •Поток вектора через поверхность
- •Вектор площадки
- •Понятие потока вектора через поверхность
- •Гидродинамический смысл потока вектора через поверхность. Поток жидкости через поверхность
- •Поток вектора через плоскую кривую l
- •Свойства и вычисление потока вектора через поверхность
- •Оператор Гамильтона «набла»
- •Дивергенция векторного поля
- •Ротор (вихрь) векторного поля
- •Потенциальное векторное поле
- •8.1 Плоское потенциальное поле
- •IV. Решение типовых задач
- •Вычисление и применение двойного интеграла
- •Вычисление и применение тройного интеграла
- •Вычисление и применение поверхностного интеграла первого рода
- •Вычисление и применение криволинейного интеграла.
- •V. Варианты контрольных работ Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Список литературы
Вычисление и применение криволинейного интеграла.
Схема решения задач
По условию задачи выбрать формулу и записать искомую величину в виде криволинейного интеграла первого или второго рода.
Выразить из уравнения кривой все переменные и их дифференциалы через одну переменную и ее дифференциал. Всё подставить в подынтегральное выражение.
Найти интервал изменения этой переменной на заданной дуге кривой и вычислить полученный определенный интеграл.
Пример 10
Вычислить
![]() если L
– дуга
если L
– дуга
![]() синусоиды
синусоиды
![]()
Решение
Для вычисления
криволинейного интеграла первого рода
найдем dl.
Из уравнения кривой
![]()
![]() Так как кривая L
не ориентирована, возьмем :
Так как кривая L
не ориентирована, возьмем :
![]() ,
y
и dl
подставим в подынтегральное выражение.
Получим и вычислим определенный интеграл.
,
y
и dl
подставим в подынтегральное выражение.
Получим и вычислим определенный интеграл.
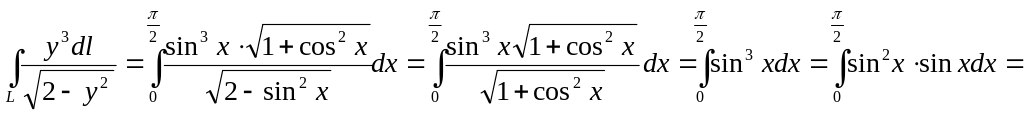
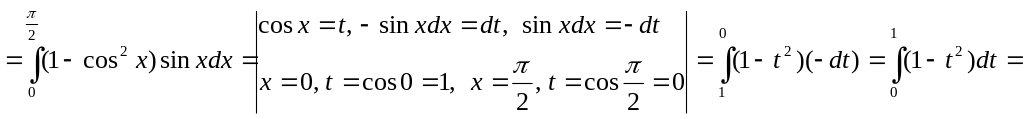
![]()
Пример 11
Вычислить
![]() по дуге кривой
по дуге кривой
![]() от
A
(1,1) до B
(-1,-1).
от
A
(1,1) до B
(-1,-1).
Решение
Для вычисления
криволинейного интеграла второго рода
выразим y
и dy
через x и
dx
из уравнения кривой
![]() В интегралах второго рода кривая
ориентирована. При движении по кривой
от A
до B
переменная
x
изменяется
от 1
до –1.
Всё подставим в подынтегральное
выражение.
В интегралах второго рода кривая
ориентирована. При движении по кривой
от A
до B
переменная
x
изменяется
от 1
до –1.
Всё подставим в подынтегральное
выражение.
![]()
Пример 12
Найти массу дуги
кривой
![]() ,
если линейная плотность массы в точке
M
(x,y)
пропорциональна длине дуги
,
если линейная плотность массы в точке
M
(x,y)
пропорциональна длине дуги
![]()
Решение
Выберем формулу
![]() ,
где
,
где
![]() -
линейная плотность массы. По условию
задачи
-
линейная плотность массы. По условию
задачи
![]() Найдем длину дуги
Найдем длину дуги
![]() .
Уравнение
.
Уравнение
![]() тогда
тогда
![]()
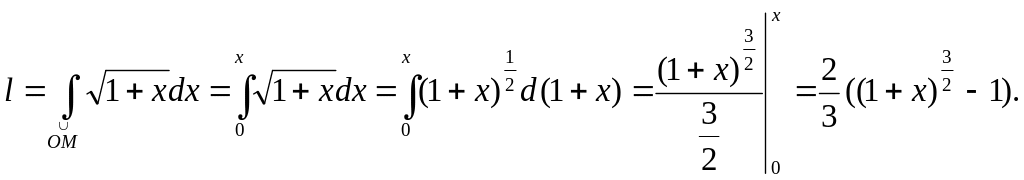
Получим
![]() ,
,
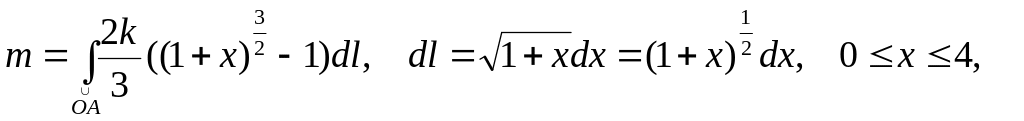 так
как
так
как
![]() и
дуги одной кривой.
и
дуги одной кривой.
![]()
![]()
Ответ:
![]()
Пример 13
Вычислить работу
силового поля
![]() при движении точки вдоль первой арки
циклоиды
при движении точки вдоль первой арки
циклоиды
![]() от
от
![]() до
до
![]() Найти
циркуляцию векторного поля
Найти
циркуляцию векторного поля
![]() вдоль замкнутого контура OBAO,
составленного из дуги
вдоль замкнутого контура OBAO,
составленного из дуги![]() циклоиды
и двух прямых OB
и BA,
если
циклоиды
и двух прямых OB
и BA,
если
![]() Найти поток вектора
через дугу
Найти поток вектора
через дугу
![]() циклоиды.
циклоиды.
Решение
Сделаем чертеж
y

 2a
A
2a
A
 B
B
0 ![]() x
x
Обозначим работу поля
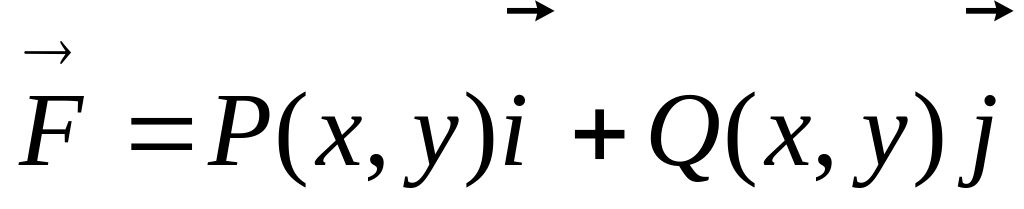 через
W
и найдем её, по формуле
через
W
и найдем её, по формуле
![]()
![]()
Из уравнения OA:
x = a (t – sin t), dx = a (1 – cos t) dt
y = a (1 – cos t), dy = a sin t dt.
В точке O (0, 0) y = 0, 0 = a (1 – cos t), cos t = 1, t = 0, в точке A (a; 2a), y = 2a,
2a = a (1 – cos t), 2 = 1 – cos t, cos t = -1, t = (обязательно проверяем получаются ли значения x в этих точках при найденных значениях t).
![]()
![]()
![]()
Найдем циркуляцию поля вдоль замкнутого контура OBAO по формуле
![]()
Контур
![]()
![]()
![]()
Из уравнения OB:
![]() получим
получим
![]() x
изменяется от
x
изменяется от
![]() до
до
![]()
![]()
![]()
Из уравнения BA:
![]() изменяется от 0
до 2a.
изменяется от 0
до 2a.
![]()
![]()
![]()
3) Найдем поток поля через кривую по формуле
![]()
![]()
![]()
=
![]()
![]()
![]()
![]()
Ответ:
![]()
Пример 14
Найти ротор и
дивергенцию векторного поля
![]() в произвольной точке M
(x,y,z)
и в точке
в произвольной точке M
(x,y,z)
и в точке
![]() .
.
Решение
По формуле
![]()
![]()
Найдем частные производные
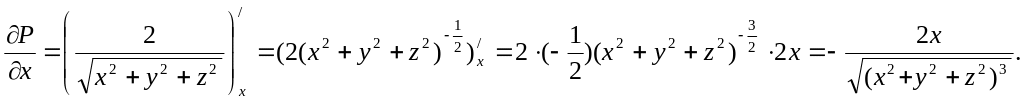
Обозначив
![]() запишем
запишем
![]() ,
,
![]()
![]()
![]() .
.
Подставим найденные производные в формулу ротора
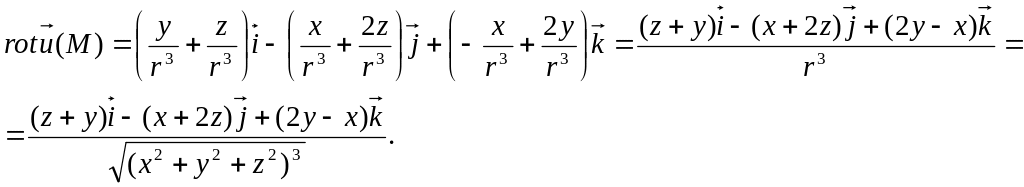
В точке
![]() (2;-2;1)
(2;-2;1)
![]()
По формуле
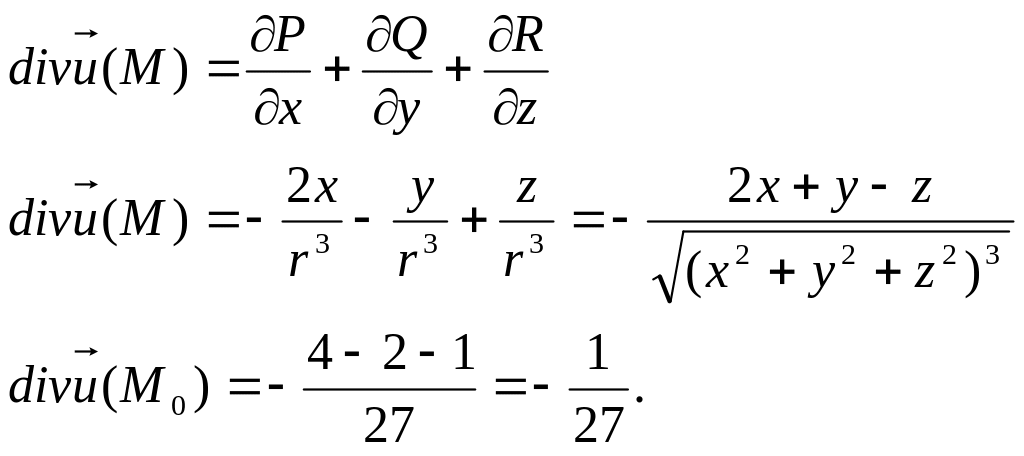
Ответ:
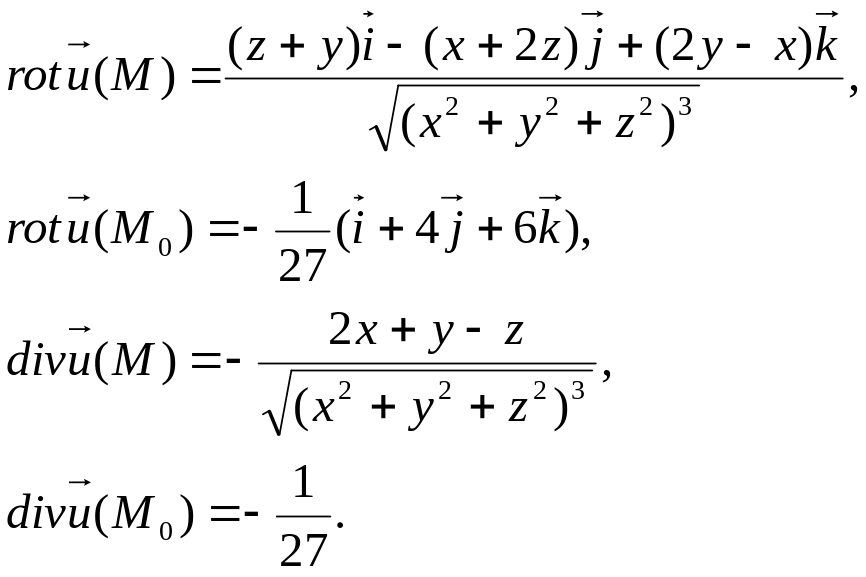
V. Варианты контрольных работ Вариант 1
1. Найти момент
инерции относительно начала координат
однородной фигуры, ограниченной линиями
xy
= 2, y
= 2x,
2y
= x
и расположенной в первой четверти
![]() если
поверхностная плотность массы
= 1.
если
поверхностная плотность массы
= 1.
Ответ:
![]() .
.
2. Найти площадь
фигуры
![]()
Ответ:
![]()
3. Найти электрический
заряд кривой
![]() если плотность заряда
если плотность заряда
![]()
Ответ:
![]()
4. Найти работу
поля
![]() при перемещении точки по эллипсу x=2cos
t,
y
= sin
t
из A
(2, 0) в B
(0,1). Найти циркуляцию
по замкнутому контуру ABDA
где D(-1,1),
BD
и DA
прямые. Найти поток вектора
через дугу
эллипса.
при перемещении точки по эллипсу x=2cos
t,
y
= sin
t
из A
(2, 0) в B
(0,1). Найти циркуляцию
по замкнутому контуру ABDA
где D(-1,1),
BD
и DA
прямые. Найти поток вектора
через дугу
эллипса.
Ответ:
![]()
5. Найти координаты центра массы однородного тела, ограниченного поверхностями x = 0, y = 0, z = 1, z = 3, 2x + y=3.
Ответ:
![]()
6. Найти массу части
сферы
![]() расположенной в первом октанте
расположенной в первом октанте
![]() если поверхностная плотность массы
если поверхностная плотность массы
![]() .
.
Ответ:
![]()
7. Найти дивергенцию
и ротор векторного поля
![]() в точке M
(x,y,z)
и в точке
в точке M
(x,y,z)
и в точке
![]()
Ответ:
![]()
