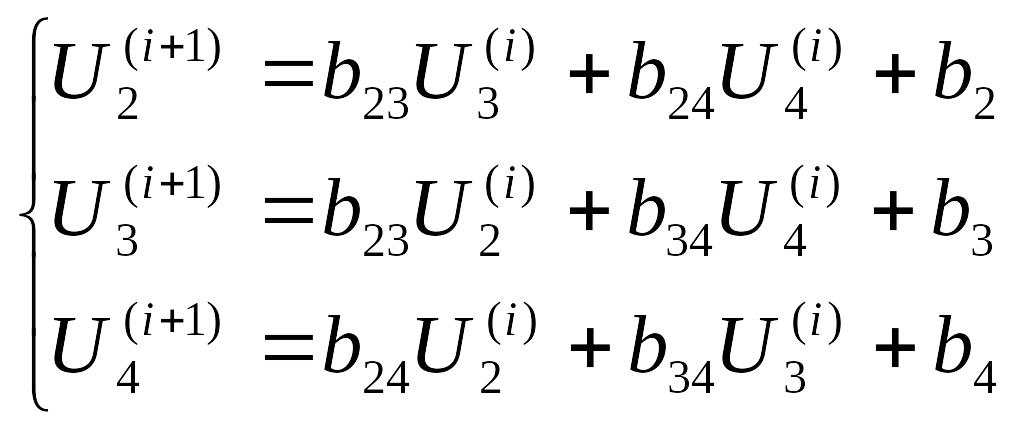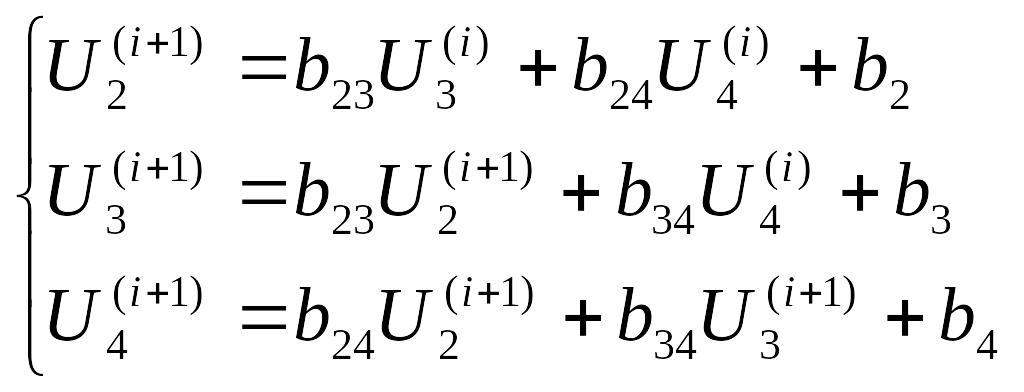Применение итерационных методов при расчете режимов электрических сетей
Методы простой итерации и ускоренной итерации (метод Зейделя) – простейшие из итерационных методов. Рассмотрение простой итерации важно для понимания сути применения итерационных методов расчета установившихся режимов электрических систем.
Рассмотрим систему уравнений третьего порядка на примере системы (5.27):
-
Y12U1 – Y22U2 + Y23U3 + Y24U4 = I2
Y13U1 + Y23U2 – Y33U3 + Y34U4 = I3
Y24U2 + Y34U3 – Y44U4 = I4
Предполагая, что диагональные элементы Y22 ≠ 0, Y33 ≠ 0, Y44 ≠ 0, разрешим первое уравнение системы относительно U2, второе – относительно U3, третье - относительно U4:
-
,
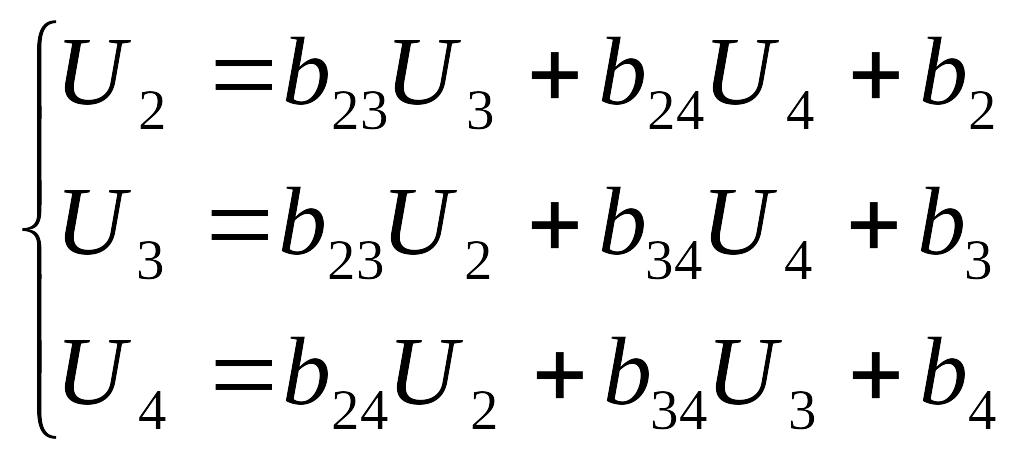коэффициенты b введены для упрощения записи системы. Например, для узла 2:
-
;
;
,
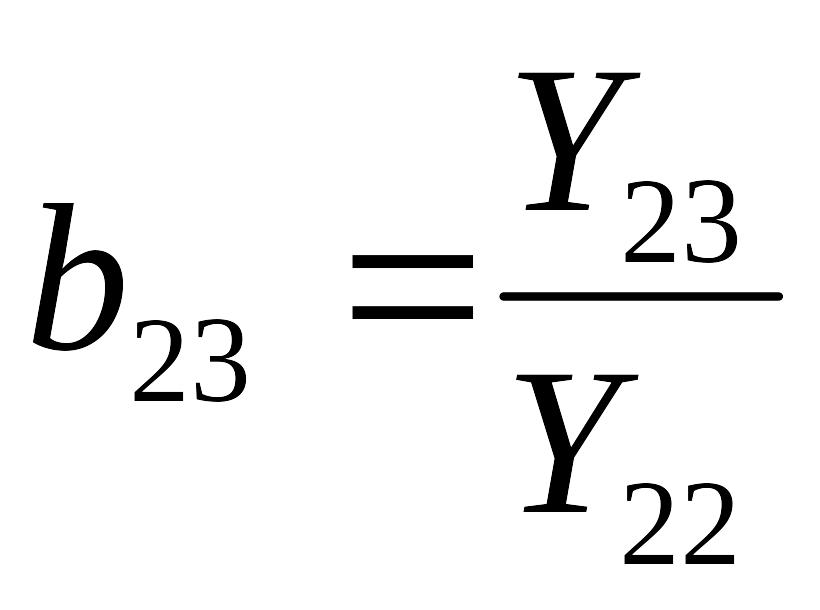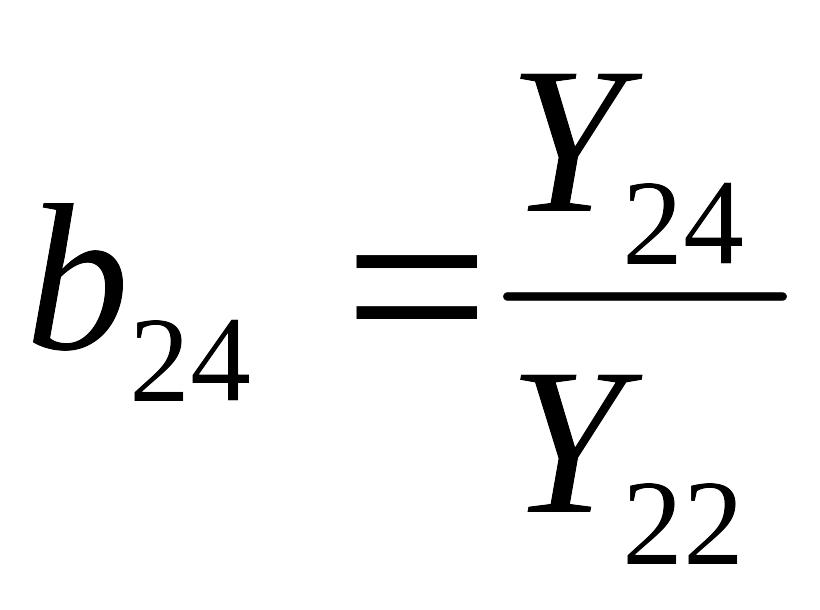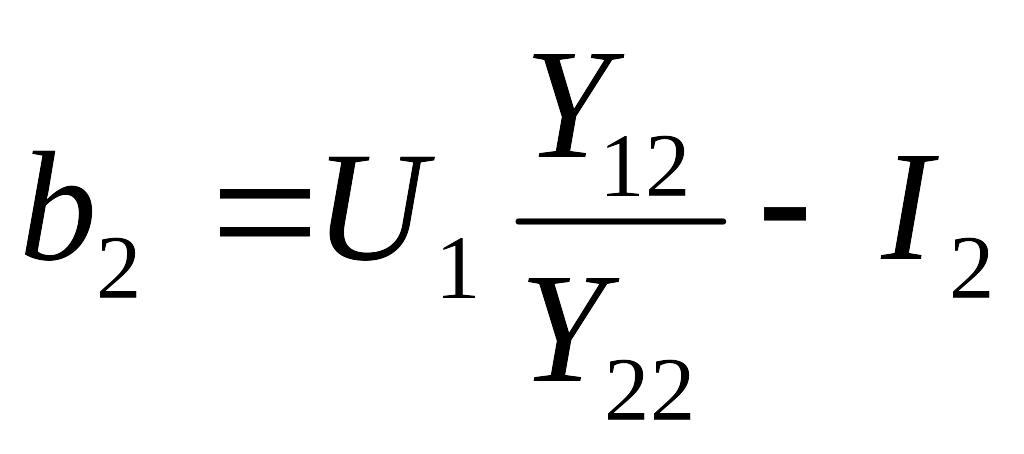то же сделано для узлов 3, 4.
Зададимся
начальным приближением неизвестных
,
,
(например,
Uном).
Подставляя их в правые части системы
(5.30), получаем первые приближения:
,
,
.
Полученные первые приближения могут
быть использованы для получения вторых,
третьих и последующих приближений.
Используя значения U2,
U3,
U4
полученные на предыдущем i-м
шаге, можно получить (i+1)-е
приближение:
Метод
Зейделя представляет собой метод
ускоренной итерации, заключающийся в
том, что найденное (i+1)-е
приближение (n-1)-го
напряжения
сразу же используется для вычисления
следующего, n-го напряжения
.
Для системы (5.31) метод Зейделя описывается следующим выражением:
В таком случае итерационный процесс сходится быстрее.
Итерационный процесс ведется до получения точного решения, но практически заранее задается точность расчета ε, и процесс ведется до достижения заданной точности:
-
,
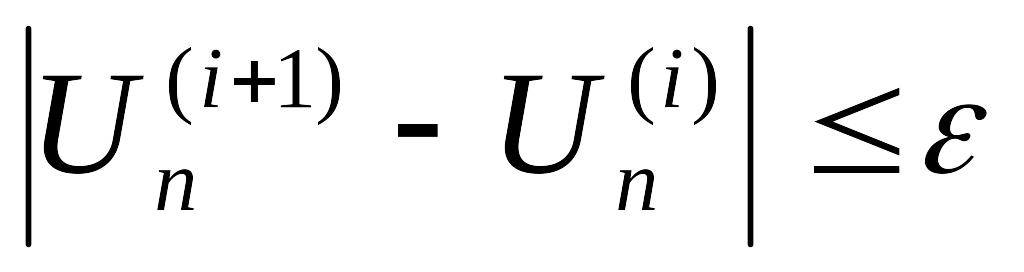т.е. пока напряжения в каждом узле, найденные на (i+1) итерации, не станут отличаться по модулю от напряжений, найденных на (i) итерации, на величину ε (например, на 0,1 кВ или 0,01 кВ – в зависимости от того, какая задана точность расчета).
На сходимость итерационного процесса влияют: сопротивления (проводимости) ветвей, напряжения и нагрузки в узлах сети, напряжение опорного узла. Итерационный процесс может сходиться по экспоненциальному или колебательному законам, а также может расходиться.
Тема 5. Регулирование напряжения и частоты в электроэнергетической системе.
Способы регулирования напряжения и частоты. Показатели качества электроэнергии.
(специалисты – 2ч., бакалавры – 2 ч.)