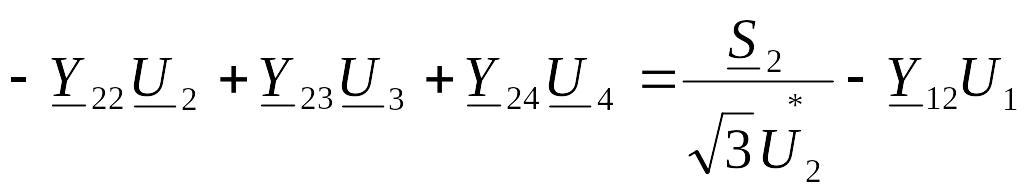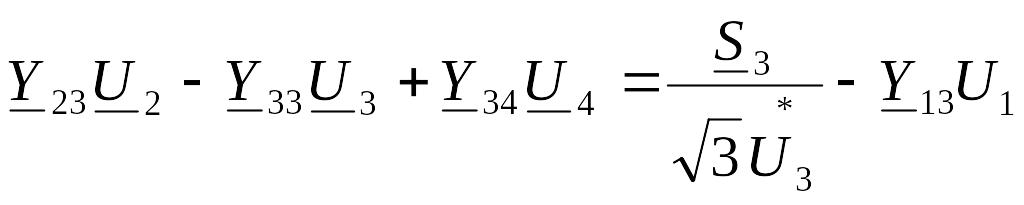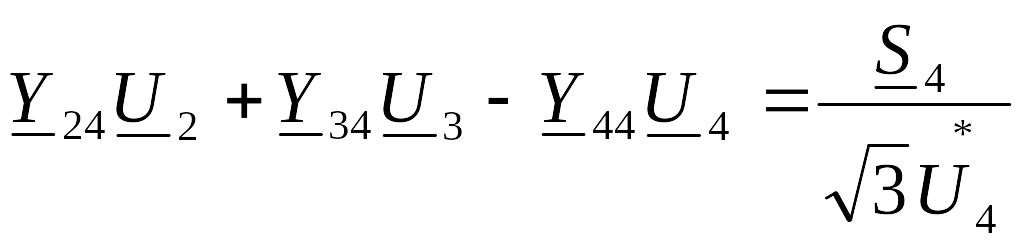Электрический расчет сети обобщенным методом контурных уравнений
Этот метод применяют для расчета замкнутых сетей разного номинального напряжения, связанных между собой трансформаторными связями (рис. 5.4).
Схема сети для расчета обобщенным методом
Если расчет ведется вручную, то перед началом расчета сопротивление линии Л3 следует привести к напряжению ВН трансформаторов по выражениям, приведенным на рис.5.4.
Если коэффициенты трансформации трансформаторов равны кт1=кт2, то расчет сети выполняется обычным методом контурных уравнений (5.9, 5.12).
Если коэффициенты трансформации не равны: кт1¹кт2, то в такой сети появляется неуравновешенная ЭДС:
-
Е=Uo(1-Пктi),
где Пктi – произведение коэффициентов трансформации трансформаторов связи, взятое в направлении обхода контура:
-
Пктi= кт1 кт2,
например:
; Uo
– напряжение опорного узла.
Под опорным узлом понимают узел, напряжение которого заранее известно и в течение расчета не изменяется.
Тогда контурные уравнения примут следующий вид:
-
.
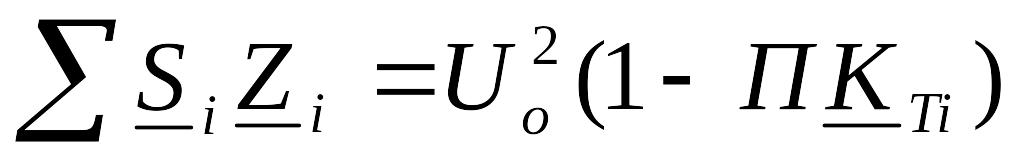Вместо уравнения (5.17) в комплексной форме можно записать уравнения в действительных числах:
-
,
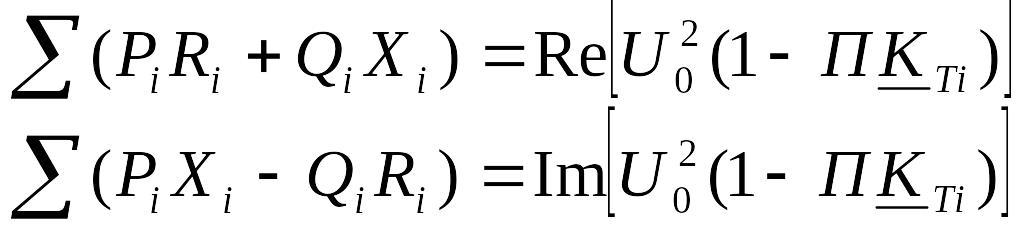здесь
в правой части уравнений содержатся
соответственно действительная
и мнимая
части уравнения (5.17).
Si=Pi-jQi – потоки мощности на участках вызваны не только нагрузками (Pнi и Qнi), но и уравнительной мощностью, которая вызвана неуравновешенной ЭДС: Sур=Pур – jQур, поэтому уравнение (5.18) можно разделить:
-
.
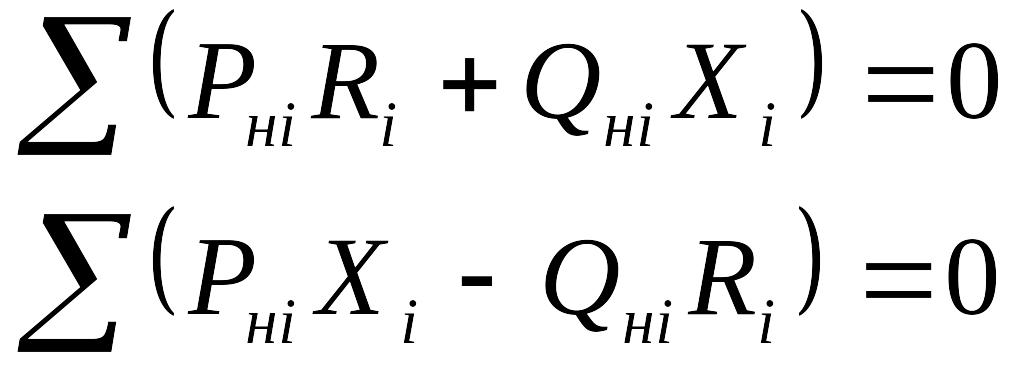
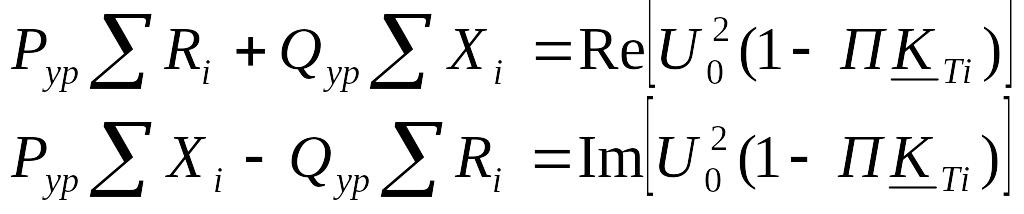Первая пара уравнений решается так же, как (5.9, 5.12). Из второй пары уравнений находится уравнительная мощность Pур – jQур. Результирующее потокораспределение находится методом наложения.
Далее порядок расчета аналогичен порядку расчета метода контурных уравнений: находятся приближенные значения потоков в ветвях (потери мощности рассчитывают по Uном), напряжения в узлах, затем уточняются потоки с учетом потерь, рассчитанных по найденным напряжениям, и рассчитываются новые значения напряжений. Расчет ведут до достижения требуемой точности.
Электрический расчет сети методом узловых напряжений
Решение задачи по определению потокораспределения от приближенного к более точному по найденным напряжениям узлов, которое использовалось в п.5.2-5.4, довольно трудоемкий процесс. Метод узловых напряжений позволяет быстрее найти напряжения в узлах Un, а по ним определить мощность в начале и конце каждого участка сети. Этот метод заложен в основу многих программ расчета установившихся режимов замкнутых электрических сетей на ЭВМ: RASTR, MUSTANG и др.
Для схемы, содержащей n узлов, рис.5.5, составляется система из (n-1) уравнений. Напряжение узла 1, базисного по напряжению (опорного узла), U1 задано.
Схема сети
Сопротивления Zij (проводимости Yij ) всех линий известны, нагрузки в узлах могут быть заданы в виде токов In или мощностей Sn:
-
.
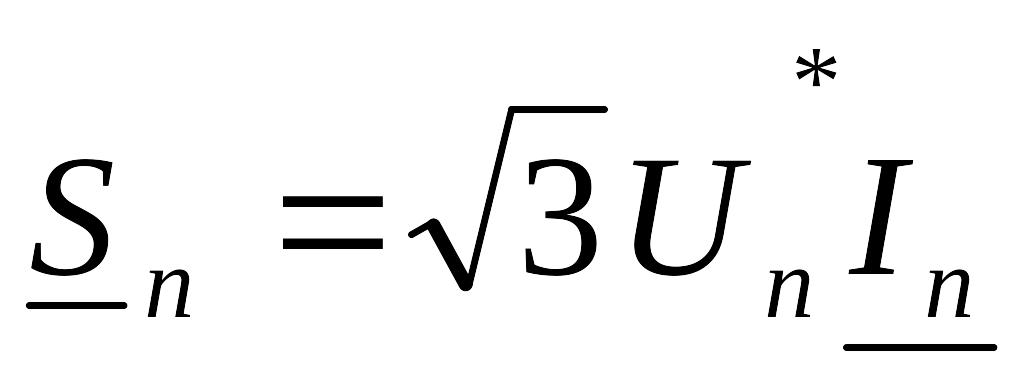Запишем взаимные проводимости узлов:
Найдем собственные проводимости узлов 2, 3, 4:
На основании 1-го закона Кирхгофа запишем векторные суммы токов в ветвях, подходящих к узлам 2, 3, 4:
Выразим токи в ветвях через узловые напряжения и проводимости ветвей:
Подставив (5.24) в (5.23), получим:
Перемножив, сгруппируем взаимные проводимости узлов 2, 3, 4:
-
Y12U1 - (Y12+Y23+Y24)U2 + Y23U3 + Y24U4 = I2
Y13U1 + Y23U2 – (Y13+Y23+Y34)U3 + Y34U4 = I3
Y24U2 + Y34U3 – (Y24+Y34)U4 = I4
В скобках системы уравнений (5.26) содержатся собственные проводимости узлов:
-
Y12U1 – Y22U2 + Y23U3 + Y24U4 = I2
Y13U1 + Y23U2 – Y33U3 + Y34U4 = I3
Y24U2 + Y34U3 – Y44U4 = I4
В системе уравнений (5.27) можно заметить, что члены уравнений, содержащие собственные проводимости узлов, расположены по диагонали и имеют знак (-).
Нагрузки в узлах электрической сети чаще задаются не токами, а мощностями (5.20), поэтому выразим правую часть (5.27) через мощности:
Решая систему уравнений (5.27 или 5.28), находят напряжения в узлах U2, U3, U4. Затем по выражению (5.23) определяют токи в ветвях, после чего по (5.20) находят мощности в начале и конце каждого участка, например,
-
мощность в начале участка 2-3:
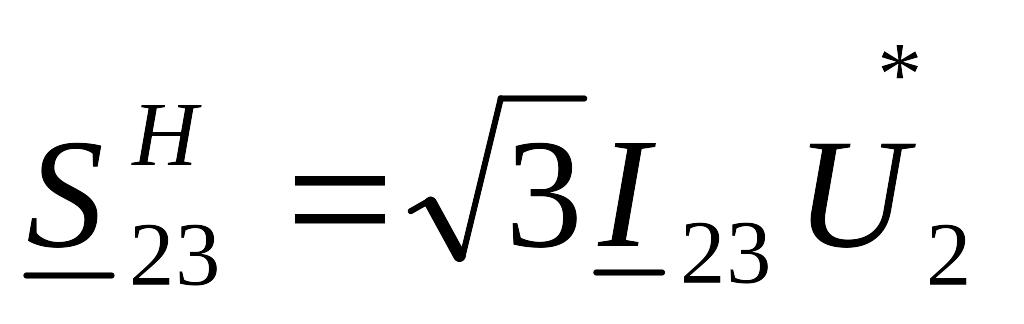
мощность в конце участка 2-3:
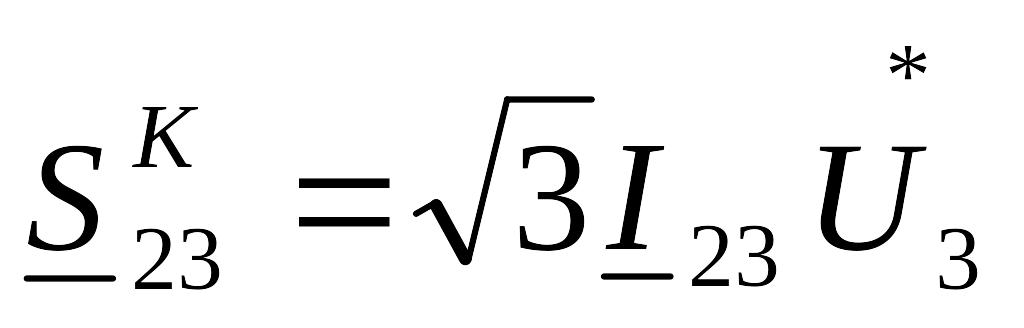
Решение системы уравнений (5.28) представляет значительную трудность, т.к. во-первых, эта система является нелинейной, во-вторых, она содержит большое число комплексных и сопряженных величин, поэтому точные методы решения такой системы уравнений не используются, и решение производят итерационными методами.