
- •Теоретичні відомості
- •2.Завдання до лабораторної роботи
- •Лабораторна робота № 3 алгоритми лінійної структури,
- •Теоретична частина
- •Завдання до лабораторної роботи
- •Лабораторна робота № 4
- •Теоретична частина
- •1. Якщо - то
- •Блок-схема:
- •Якщо - то – інакше
- •Блок-схема:
- •Блок-схема
- •Лабораторна робота № 5
- •Теоретична частина
- •Блок-схема
- •Блок-схема
- •Блок-схема
- •Лабораторна робота №6 Робота з вказівниками
- •1.Теоретична частина
- •2.Завдання до лабораторної роботи
- •Лабораторна робота №7 Основні поняття об’єктно-орієнтованого програмування
- •1.Теоретична частина
- •2. Завдання до лабораторної роботи
Практична робота
1. Перевести в десяткову систему
а) 10110112; |
е) 5178; |
л) 1F16; |
б) 101101112; |
ж) 10108; |
м) ABC16; |
в) 0111000012; |
з) 12348; |
н) 101016; |
г) 0,10001102; |
и) 0,348; |
о) 0,А416; |
д) 110100,112; |
к) 123,418; |
п) 1DE,C816. |
2. Перевести з десяткової системи в двійкову, вісімкову і шістнадцяткову системи числення
а) 123; |
е) 21.16; |
б) 232; |
ж) 56,98; |
в) 87; |
з) 34,74; |
г) 46; |
и) 4,34; |
д) 138; |
к) 123,41; |
3. Перевести з двійкової систему у вісімкову і шістнадцяткову
а) 1001111110111,01112; |
г) 1011110011100,112; |
ж)1011100110111,01112; |
б) 1110101011,10111012; |
д) 10111,11111011112; |
з)10100,11111002; |
в) 10111001,1011001112; |
е) 1100010101,110012. |
и)1101010101,100012 |
4. Додати числа у відповідних системах числення і виконати перевірку результату у десятковій системі
а) 10111012 і 11101112; |
д) 378 і 758; |
и) A16 і F16; |
б) 1011,1012 і 101,0112; |
е) 1658 і 378; |
к) 1916 і C16; |
в) 10112, 112 і111,12; |
ж) 7,58 і 14,68; |
л) A,B16 і E,F16; |
г) 10112 , 11,12 і 1112; |
з) 68, 178 і 78; |
м) E16, 916 і F16. |
5. Виконати віднімання
а) 1112 з 101002; |
д) 158 з 208; |
и) 1А16 з 3116; |
б) 10,112 з 100,12; |
е) 478 з 1028; |
к) F9E16 з 2А3016; |
в) 111,12 з 100102; |
ж) 56,78 з 1018; |
л) D,116 з B,9216; |
г) 100012 з 1110,112; |
з) 16,548 з 30,018; |
м) ABC16 з 567816. |
6. Виконати множення
а) 1011012 и 1012; |
д) 378 и 48; |
б) 1111012 и 11,012; |
е) 168 и 78; |
в) 1011,112 и 101,12; |
ж) 7,58 и 1,68; |
г) 1012 и 1111,0012; |
з) 6,258 и 7,128. |
Варіанти
№ |
З.1 |
З.2 |
З.3 |
З.4 |
З.5 |
З.6 |
1 |
а,е,л |
А,е |
А,г,ж |
Г,ж,л |
А,з,и |
Б,е |
2 |
Г,з,м |
Б.ж |
Б,д,з |
В,е,з |
Б,е,к |
В,ж |
3 |
В,з,н |
В,з |
В,е,и |
В,д,и |
Б,д,и |
Г,з |
4 |
Д,о,п |
Г,и |
А,е,з |
а,е,л |
А,д,к |
А,д |
5 |
В,и,о |
Д,к |
Б,в,ж |
Б,е,к |
а,д,м |
Б,з |
6 |
Д,к,л |
А,ж |
Б,д,и |
Б,ж,м |
Г,з,м |
А,ж |
7 |
Г,и,о |
Б,з |
Г,з,м |
В,ж,и |
В,ж,л |
Б,ж |
8 |
а,д,м |
Г,к |
А,д,м |
Г,з,м |
Г,е,л |
А,е |
9 |
Б,ж,л |
Д,е |
В,д,к |
А,з,и |
В,е,з |
Г,е |
Лабораторна робота №1
Основи алгебри логіки
Теоретичні відомості
1.Алгебра логіки
Алгебра логіки — це розділ математики, що вивчає висловлення, розглянуті з точки зору їхніх логічних значень (істинності або хибності) і логічних операцій над ними.
Логічне висловлення — це будь-яка оповідальне речення, у відношенні якого можна однозначно сказати, істинне воно або хибне. Щоб звертатися до логічних висловлень, їм призначають імена.
Операції над логічними висловленнями:
НЕ Операція, що виражається словом "не", називається запереченням і позначається рискою над висловленням (або знаком ). Висловлення істинне, коли A хибне, і хибне, коли A істинне.
І Операція, що виражається зв'язуванням "і", називається кон’юнкцією (лат. conjunctio — з'єднання) або логічним множенням і позначається точкою " " (може також позначатися знаками або &). Висловлення А·В істинно тоді і тільки тоді, коли обидва висловлення А и В істинні.
АБО Операція, що виражається зв'язуванням "або" (у невиключаючому сенсі ) називається диз'юнкцією (лат. disjunctio — поділ) або логічним додаванням і позначається знаком v (або плюсом). Висловлення А v В помилкове тоді і тільки тоді, коли обидва висловлення А и В помилкові.
ЯКЩО-ТО Операція, що виражається зв'язуваннями "якщо ..., то", "з ... випливає", "... витікає ...", називається імплікацією (лат. implico — тісно зв'язані) і позначається знаком . Висловлення помилкове тоді і тільки тоді, коли А істинно, а В хибне.
РІВНОСИЛЬНА Операція, що виражається зв'язуваннями "тоді і тільки тоді", "необхідно і досить", "... рівносильно ...", називається еквіваленцією або подвійною імплікацією і позначається знаком або ~. Висловлення істинне тоді і тільки тоді, коли значення А и В збігаються.
За допомогою логічних змінних і символів логічних операцій будь-яке висловлення можна формалізувати, тобто замінити логічною формулою.
В алгебрі логіки виконуються наступні основні закони, що дозволяють робити тотожні перетворення логічних виражень:
Рівносильні перетворення логічних формул мають те ж призначення, що і перетворення формул у звичайній алгебрі. Вони служать для спрощення формул або приведення їх до визначеного виду шляхом використання основних законів алгебри логіки.
Під спрощенням формули, що не містить операцій імплікації і еквіваленції, розуміють рівносильне перетворення, що приводить до формули, що або містить у порівнянні з вихідною менше число операцій кон’юнкції і диз'юнкції і не містить заперечень неелементарних формул, або містить менше число входжень змінних.
Закон |
Для АБО |
Для І |
Комутативний |
|
|
Асоціативний |
|
|
Дистрибутивний |
|
|
Правила де Моргана |
|
|
Тавтології |
|
|
Поглинання |
|
|
Склеювання |
|
|
Операція над змінною з її інверсією |
|
|
Правила операцій з константами |
|
|
Закон подвійного заперечення |
|
|
Приклади
1.
![]()
2.
![]()
3.
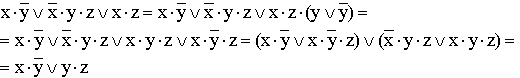
4.
![]()
5.
![]()
6.
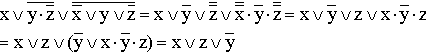
7.
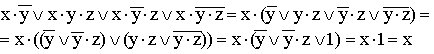
8.
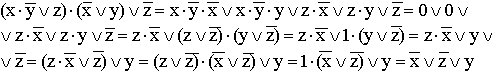
9.
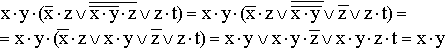
2.Перемикальні схеми
У комп'ютерах і інших автоматичних пристроях широко застосовуються електричні схеми, що містять сотні і тисячі перемикальних елементів: реле, вимикачів і т.п. Розробка таких схем досить трудомістка справа. Виявилося, що тут з успіхом може бути використаний апарат алгебри логіки.
Перемикальна схема — це схематичне зображення деякого пристрою, що складає з перемикачів і з'єднуючих провідників, а також із входів і виходів, на які подається і з яких знімається електричний сигнал.
Кожен перемикач має тільки два стани: замкнутий і розімкнутий. Перемикачеві Х поставимо у відповідність логічну перемінну х, що приймає значення 1 у тому і тільки в тому випадку, коли перемикач Х замкнути і схема проводить струм; якщо ж перемикач розімкнути, то х дорівнює нулеві.
Усій перемикальній схемі також можна поставити у відповідність логічну змінну, рівну одиниці, якщо схема проводить струм, і рівну нулеві — якщо не проводить. Ця змінна є функцією від змінних, відповідних усім перемикачам схеми, і називається функцією провідності.
Дві схеми називаються рівносильними, якщо через одну з них проходить струм тоді і тільки тоді, коли він проходить через іншу (при тому самому вхідному сигналі).
З двох рівносильних схем більш простою вважається та схема, функція провідності якої містить менше число логічних операцій або перемикачів.
При розгляді перемикальних схем виникають дві основні задачі: синтез і аналіз схеми.
СИНТЕЗ СХЕМИ по заданих умовах її роботи зводиться до наступних трьох етапів:
складанню функції провідності по таблиці істинності, що відбиває ці умови;
спрощенню цієї функції;
побудові відповідної схеми.
АНАЛІЗ СХЕМИ зводиться до
визначенню значень її функції провідності при всіх можливих наборах вхідних у цю функцію перемінних.
одержанню спрощеної формули.
Приклади.
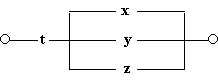
1. Побудуємо схему, що містить 4 перемикачі x, y, z і t, таку, щоб вона проводила струм тоді і тільки тоді, коли замкнути контакт перемикача t і який-небудь з інших трьох контактів.
Рішення. У цьому випадку можна обійтися без побудови таблиці істинності. Очевидно, що функція провідності має вигляд F(x, y, z, t) = t · (x v y v z), а схема виглядає так:
Приклад 2
Проаналізувати задану схему
![]()
Розв’язок
![]()
![]()
В даному випадку будувати таблицю істинності не потрібно.
Приклад 3
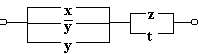
Розв’язок
![]()
Спрощена перемикальна схема
![]()
Таблиця істинності
z |
t |
F |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
3.Логічний елемент комп'ютера — це частина електронної логічної схеми, що реалізує елементарну логічну функцію.
Логічними елементами комп'ютерів є електронні схеми І, АБО, НЕ, І-НЕ, АБО-НЕ й інші (звані також вентилями), а також тригер.
За допомогою цих схем можна реалізувати будь-яку логічну функцію, що описує роботу пристроїв комп'ютера. Звичайно у вентилів буває від двох до восьми входів і один або два виходи.
Високий рівень звичайно відповідає значенню “істина” (“1”), а низький — значенню “неправда” (“0”).
Кожен логічний елемент має свою умовну позначку, що виражає його логічну функцію, але не вказує на те, яка саме електронна схема в ньому реалізована. Це спрощує запис і розуміння складних логічних схем.
Роботу логічних елементів описують за допомогою таблиць істинності.
Таблиця істинності -це табличне представлення логічної схеми (операції), у якому перераховані всі можливі сполучення значень істинності вхідних сигналів (операндів) разом зі значенням істинності вихідного сигналу (результату операції) для кожного з цих сполучень.
Схема І
Схема І реалізує кон’юнкцію двох або більше логічних значень.
Одиниця на виході схеми І буде тоді і тільки тоді, коли на усіх входах будуть одиниці. Коли хоча б на одному вході буде нуль, на виході також буде нуль.
Зв'язок між виходом z цієї схеми і входами x і y описується співвідношенням: z = x · y
(читається як "x і y"). Операція кон’юнкції на структурних схемах позначається знаком "&" (читається як "амперсенд"), що є скороченим записом англійського слова and.
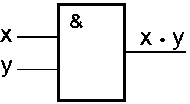
Схема АБО
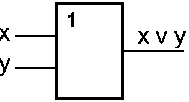
Схема АБО реалізує диз'юнкцію двох або більш логічних значень. Коли хоча б на одному вході схеми АБО буде одиниця, на її виході також буде одиниця.
Умовна позначка на структурних схемах схеми АБО з двома входами представлене на мал. 5.2. Знак "1" на схемі — від застарілого позначення диз'юнкції як ">=1" (тобто значення диз'юнкції дорівнює одиниці, якщо сума значень операндів більше або дорівнює 1). Зв'язок між виходом z цієї схеми і входами x і y описується співвідношенням: z = x v y (читається як "x або y").
С х е м а НЕ
Схема НЕ (інвертор) реалізує операцію заперечення. Зв'язок між входом x цієї схеми і виходом z можна записати співвідношенням z = , x де читається як "не x" або "інверсія х".
Якщо на вході схеми 0, то на виході 1. Коли на вході 1, на виході 0.
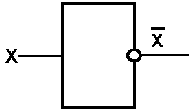
Схема І-НЕ
Схема І-НЕ складається з елемента І и інвертора і здійснює заперечення результату схеми І. Зв'язок між виходом z і входами x і y схеми читається як "інверсія x і y".
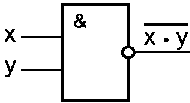
Схема АБО-НЕ
Схема АБО-НЕ складається з елемента АБО й інвертора і здійснює заперечення результату схеми АБО. Зв'язок між виходом z і входами x і y схеми читається як "інверсія x або y ".

