Математические свойства дисперсии

1. Если из всех значений вариант отнять какое-то постоянное число А, то средний квадрат отклонений от этого не изменится:

.

2. Если все значения вариан разделить на какое-то постоянное число А, то средний квадрат отклонений уменьшится от этого в раз, а среднее квадратическое отклонение – в А раз:

3. Если исчислить средний квадрат отклонений от любой величины (А), отличающейся от средней арифметической , то он всего будет больше среднего квадрата отклонений, исчисленного от средней арифметической:

.

Причем больше на определенную величину – на квадрат разности между средней и этой условно взятой величиной, т.е. на

Таким образом,

или

где - средний квадрат отклонений от средней арифметической ;

- средний квадрат отклонений от произвольной величины (А).

Значит, дисперсия от средней всегда меньше дисперсий, исчисленных от любых других величин, т.е. она обладает свойством минимальности.

4. Если А = 0, то

или .

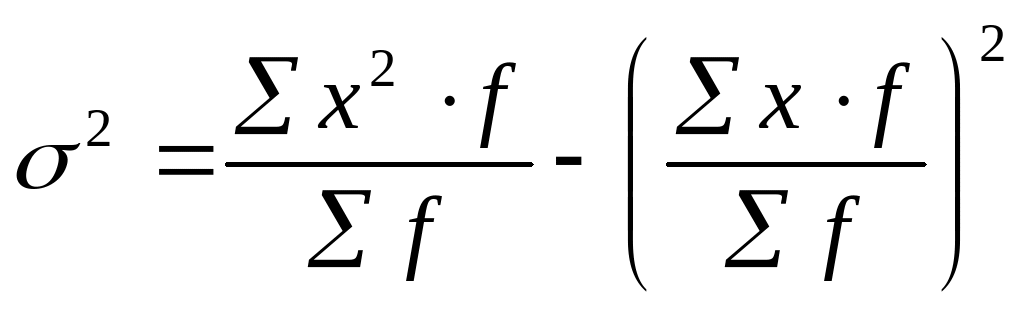или

Средний квадрат отклонений равен среднему квадрату значений признака минус квадрат среднего значения признака.

Этой формулой расчета дисперсии пользуются более широко, особенно при машинной обработке данных.

Пример 3. Расчет дисперсии по формуле:

Произведено продук-ции ра-бочими, шт. Х	Число рабочих f
8	7	56	64	448
9	10	90	81	810
10	15	150	100	1500
11	12	132	121	1452
12	6	72	144	864
Итого	50	500	510	5074

Порядок расчета дисперсии :

1. Определяется средняя арифметическая по формуле: ;

2. Возводится в квадрат средняя арифметическая:

;

3. Возводится в квадрат каждая варианта ряда: ;

4. Перемножаются квадраты вариант на частоты:

;

5) Найти сумму произведения квадратов вариант на частоты: ;

6) Разделить сумму произведения квадратов вариант на частоты на сумму частот:

7) Определяют разность между средней из квадратов вариант и квадратом средней:

;

Виды дисперсий

Дисперсия – это показатель вариации, выражающий средний квадрат отклонений вариантов от средней величины. В зависимости от образующих вариацию факторов различают общую, межгрупповую и внутригрупповую дисперсию.

1.Общая дисперсия - образуется под вилянием совокупного действия всех факторов на изучаемое явление. Общая дисперсия определяется по формулам:

а) невзвешенной - ;

б) взвешенной - .

2.Межгрупповая дисперсия - характеризует влияние на колеблемость изучаемого признака лишь группировочного признака.Она представляет собой средний квадрат отклонения групповых средних от общей средней :

.

- групповые средние;

- число единиц в группах;

- общая средняя.

3.Внутригрупповая дисперсия - характеризует в группах статистической совокупности влияние на колеблемость изучаемого признака прочих факторов, кроме группировочного. Это вариация, которая осталась в группах после расчленения статистической совокупности на однородные группы.

Частные или внутригрупповые дисперсии – это дисперсии, вычисленные для каждой группы совокупности. Служат они для характеристики рассеяния признака в каждой группе:

а) невзвешенные - ;

б) взвешенные –

,

где - суммирование по каждой группе.

Обобщающей характеристикой внутри-групповой дисперсии является средняя внутригрупповая дисперсия :

.

Между общей, межгрупповой и средней внутригрупповой дисперсией имеется зависимость, которая выражается формулой: