Задание № 3 Плоский изгиб прямых брусьев.

Для заданных двух расчетных схем балок (рис. 3) требуется написать выражения для поперечных сил и изгибающего момента для каждого участка в общем виде, построить эпюры и , найти и подобрать:

а) для схемы а деревянную балку круглого и прямоугольного поперечного сечения при =10 МПа;

б) для схемы б стальную балку двутаврового поперечного сечения при =160 МПа.

Для подобранных сечений построить эпюру .

Исходные данные взять в таблице 3

Таблица 3

№ п/п	Схема	, м	, кН	, кН/м	, кНм
	В	Б	В	А	В
0	X	2	6	2	8
1	I	2	10	2	4
2	II	1	12	4	6
3	III	3	8	5	8
4	IV	2	14	3	10
5	V	3	15	2	8
6	VI	2	10	3	6
7	VII	2	12	4	10
8	VIII	1	14	5	8
9	IX	3	8	4	6

Порядок расчета

1. Находим реакции опор (только для схемы б).

2. Разбиваем схему на участки.

3. Составляем выражения для Q и М на каждом из участков.

4. Строим эпюры Q и М (в масштабе).

5. Определяем размеры поперечного сечения балки из условия прочности по нормальным напряжениям.

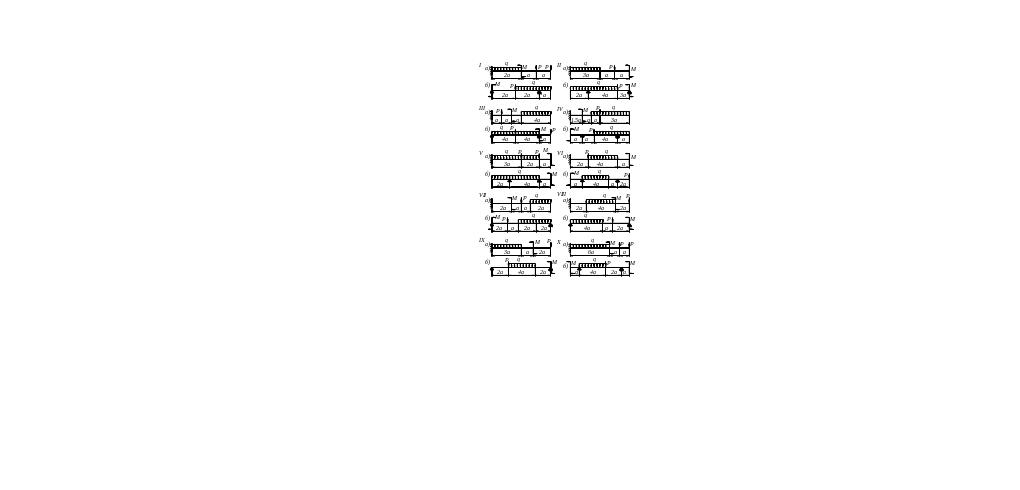
Рисунок 3 Расчетные схемы.

Пример решения 2а

= 3 кН/м; =8 кНм; =6 кН; а = 3м; = 2; = 10 МПа.

Определить: размеры прямоугольного и круглого поперечного сечения.

Решение

1. Разбиваем схему на участки.

Разбиваем заданную схему на участки. Наша расчетная схема состоит из 3 участков: первый – АВ; второй – ВС и третий – CD.

2. Составляем выражения для Q и М на каждом из участков.

Определяем значения и на границах участков и в характерных точках.

Участок I

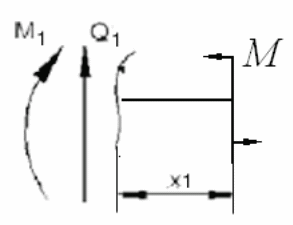
Q₁ = 0.

;

Участок II

;

;

;

;

;

Участок III ;

;

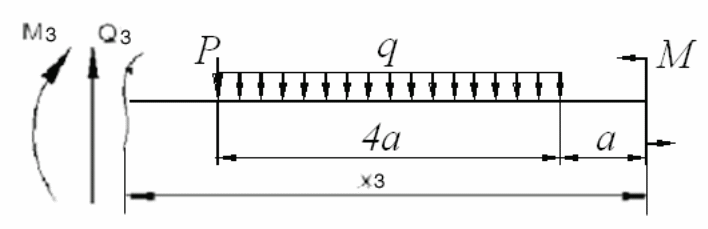
3. Строим эпюры Q и М (в масштабе).

По полученным данным строим эпюры и

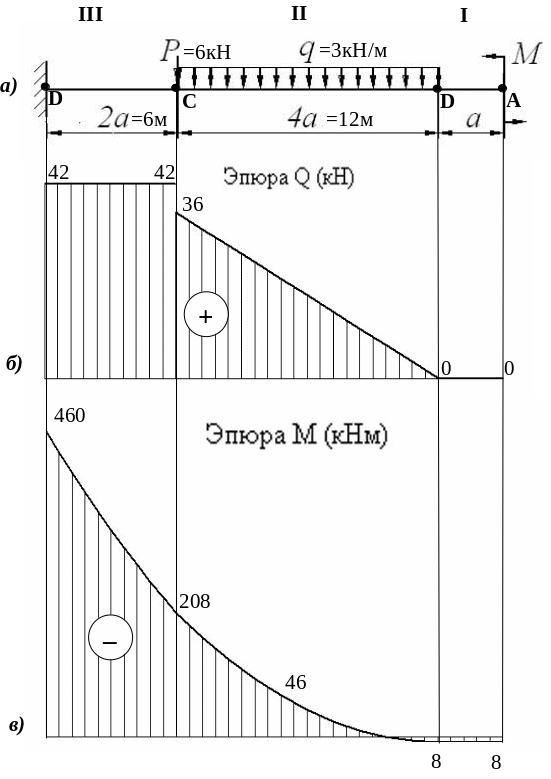Графическая часть задания №2а

6. Определяем размеры поперечного сечения балки из условия прочности по нормальным напряжениям.

Величина максимального изгибающего момента равна .

Определим размеры поперечного сечения балки, используя условие прочности при изгибе.

а) прямоугольное сечение ;

– осевой момент сопротивления для прямоугольного сечения, учитывая заданное соотношение сторон: , получим:

,

;

Округляя принимаем:

;

б) круглое сечение

– осевой момент сопротивления для круглого сечения.

Округляя, принимаем .

Пример решения задачи 2 б

Исходные данные к расчету:

= 3 кН/м; =8 кНм; =6 кН; а = 3м; = 160 МПа.

Решение

1. Определяем реакции опор заданной схемы

;

;

.

;

;

.

Проверка

.

2. Разбиваем схему на участки.

Разбиваем заданную схему на участки. Наша расчетная схема состоит из 4 участков: первый – BE; второй – DB, третий – CA и четвертый – AD.

3. Составляем выражения для Q и М на каждом из участков.

Определяем значения и на границах участков и в характерных точках.

Участок I

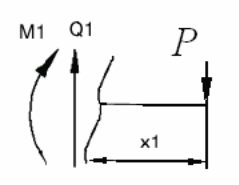
Q₁ = Р = 6 кН.

;

Участок II

;

;

;

Участок III ;

;

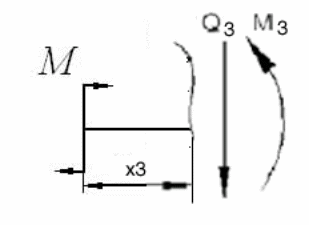
Участок IV ;

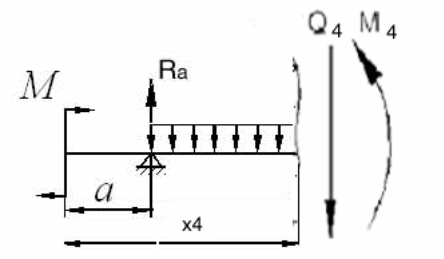
Найдем точку, в которой (в этой точке момент приобретает экстремальное значение)

;

4. Строим эпюры Q и М (в масштабе).

По полученным данным строим эпюры и

6. Определяем размеры поперечного сечения балки из условия прочности по нормальным напряжениям.

Величина максимального изгибающего момента равна .

Определим размеры поперечного сечения балки, используя условие прочности при изгибе.

Размеры сечения двутавровой балки определяем из таблицы сортаментов

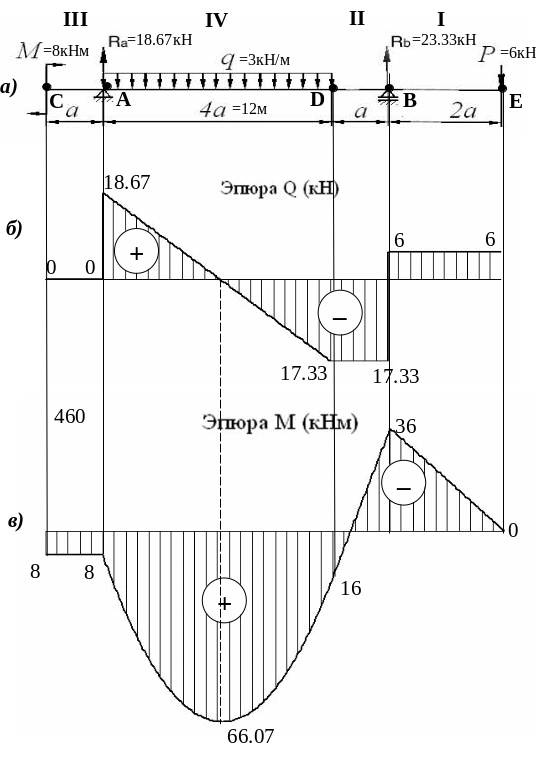
Графическая часть задания 2б