КАФЕДРА ТЕОРЕТИЧНОЇ ТА БУДІВЕЛЬНОЇ МЕХАНІКИ

Методичні ВКАЗІВКИ

до самостійного вивчення та виконання контрольної роботи з дисципліни "ОПІР МАТЕРІАЛІВ" (для студентів спеціальності 6.090200

"Гірниче обладнання"

Затверджено

на засіданні кафедри ТІБ

Протокол № _ від __.__.2007

Рекомендовано

на засіданні методичної ради ДГМІ

Протокол № _ від __.__.2007

Алчевськ, 2007

Содержание

КАФЕДРА ТЕОРЕТИЧНОЇ ТА БУДІВЕЛЬНОЇ МЕХАНІКИ 1

Методичні ВКАЗІВКИ 1

до самостійного вивчення та виконання контрольної роботи з дисципліни "ОПІР МАТЕРІАЛІВ" (для студентів спеціальності 6.090200 1

"Гірниче обладнання" 1

Содержание 2

Общие рекомендации к выполнению заданий. 3

Выбор варианта задания. 3

Требования к оформлению заданий. 4

Задание №1 Статически неопределимая задача на растяжение-сжатие прямых стержней. 5

Задание №2 Геометрические параметры плоских сечений. 15

Задание № 3 Плоский изгиб прямых брусьев. 24

Приложение А. Образец титульного листа для студентов заочной формы образования. 34

Общие рекомендации к выполнению заданий. Выбор варианта задания.

Студент выполняет номера заданий, которые предусмотрены учебным планом.

Ключом к выбору варианта задания является личный номер (для студентов очной формы обучения это номер студенческого билета, для студентов заочной формы обучения это номер зачетной книжки). В этом номере используется три последние цифры, которым ставится в соответствие первые три буквы русского алфавита: А, Б и В.

Пример. Номер студенческого билета 8009306.Последние три цифры – 306 ставим им в соответствие первые три буквы алфавита:

3	0	6
А	Б	В	,

т.е. А=3, Б=0 и В=6.

Исходные данные к заданиям представлены в виде таблиц, при этом каждый столбец таблицы определяет какой-либо из параметров задачи и ему в соответствие ставится одна из букв А, Б или В. Строки имеют нумерацию от 0 до 9. Для выбора данных соответствующих своему варианту необходимо взять данные из строки номер которой определяется цифрой соответствующей букве столбца.

Пример. Пусть первый столбец имеет шифр А, в нашем случае букве А ставится в соответствие цифра 3 следовательно в этом столбце данные берутся из строки с номером 3. Если второй столбец имеет шифр В то данные возьмем из строки с номером 6 поскольку букве В соответствует цифра 6.

Требования к оформлению заданий.

Задания оформляются на листах А4 с соблюдением следующих полей: справа – 2,5 см., слева –1,5 см., верх и низ по 2 см.. Листы имеют сквозную нумерацию в правом верхнем углу. Рамки чертить не обязательно.

Задание должно начинаться с титульного листа. Для студентов очной формы обучения каждое задание имеет свой титульный лист (образец в приложении А). Студенты заочной формы обучения оформляют все задания в виде единого документа (образец в приложении Б). На титульном листе обязательно указывается ФИО, группа и индивидуальный номер (полностью).

При оформлении заданий следует придерживаться оформления сходного с примером выполнения, которым сопровождается каждое из заданий в данном методическом указании.

Перед решением каждой задачи необходимо выписать полностью ее условие с числовыми данными, составить аккуратный эскиз расчетной схемы и указать на нем величины, необходимые для расчета.

Решение должно сопровождаться краткими объяснениями и чертежами, на которых входящие в расчет величины должны быть показаны в числах. Необходимо выделять окончательные результаты.

Задание №1 Статически неопределимая задача на растяжение-сжатие прямых стержней.

Стальной брус (Е=2∙10⁵МПа, []=160МПа), оба конца которого жестко заделаны, находится под действием сил Р1, Р2 (рис. 1). Построить эпюры продольных сил N, нормальных напряжений σ и перемещений Δ. Данные взять из таблицы 1.

Порядок расчета

1. Составить расчетную схему задания, с указанием величин необходимых для выполнения расчета.

2. Определить степень статической неопределимости задачи.

3. Записать уравнения равновесия бруса.

4. Записать полное удлинение бруса через сумму удлинений его участков (поскольку брус жестко заделан с обеих концов его полное удлинении равно 0).

5. Выразить удлинение каждого из участков через внутренние усилия, действующие на этом участке.

6. Получить выражение для определения продольной силы на каждом из участков (положительное направление продольной силы берем таким образом, что бы она вызывала растяжение участка).

7. Подставить полученные выражения в уравнение совместности деформаций полученное на IV этапе.

8. Решить систему из двух уравнений (уравнения равновесия и уравнения совместности деформаций) и определить реакции жестких заделок.

9. Построить эпюры продольных сил и нормальных напряжений.

10. Определить удлинения участков и построить эпюру перемещений.

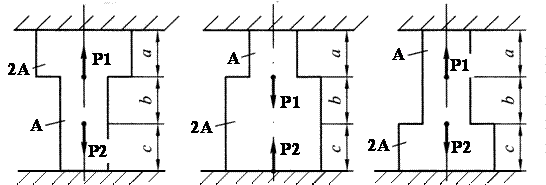
I II III

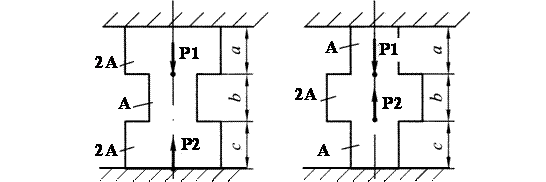
IV V

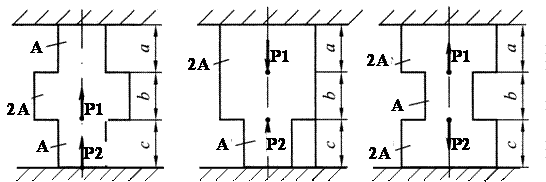
VI VII VIII

IX X

Рисунок 1 Расчетные схемы к заданию № 1

Таблица 1

№ строки	Схема на рис. 2.1	А, см2	a, м	b, м	c, м	P1, кH	P2, кH
	В	Б	А	В	Б	В	Б
0	X	20	0,2	0,11	0,3	20	24
1	I	11	0,11	0,2	0,21	11	32
2	II	12	0,12	0,19	0,22	12	45
3	III	13	0,13	0,18	0,23	13	39
4	IV	14	0,14	0,17	0,24	14	25
5	V	15	0,15	0,16	0,25	15	18
6	VI	16	0,16	0,15	0,26	16	54
7	VII	17	0,17	0,14	0,27	17	48
8	VIII	18	0,18	0,13	0,28	18	33
9	IX	19	0,19	0,12	0,29	19	26

Пример выбора варианта задания №1

В нашем случае А=3, Б=0 и В=6, поэтому мы выбираем следующие данные из таблицы (рис. 2.2, выделено черным цветом).

№ строки	Схема на рис. 2.1	А, см2	a, м	b, м	c, м	P1, кH	P2, кH
	В=6	Б=0	А=3	В=6	Б=0	В=6	Б=0
0	X	20	0,2	0,11	0,3	20	24
1	I	11	0,11	0,2	0,21	11	32
2	II	12	0,12	0,19	0,22	12	45
3	III	13	0,13	0,18	0,23	13	39
4	IV	14	0,14	0,17	0,24	14	25
5	V	15	0,15	0,16	0,25	15	18
6	VI	16	0,16	0,15	0,26	16	54
7	VII	17	0,17	0,14	0,27	17	48
8	VIII	18	0,18	0,13	0,28	18	33
9	IX	19	0,19	0,12	0,29	19	26

Рисунок 2.2 Выбор варианта задания

Следовательно, расчетная схема номер VI

Остальные исходные данные следующие:

А=20см², а=0,13м, b=0,15м, с=0,3м, Р1=16кН, Р2=24кН.

Пример выполнения задания №1.

Исходные данные к расчету:

А=20см2, а=0,13м, b=0,15м, с=0,3м, Р1=16кН, Р2=24кН.

Построить эпюры продольных сил N, нормальных напряжений σ и перемещений Δ. Данные взять из таблицы 1.

Решение

1. Составим расчетную схему.

Расчетная схема бруса представлена на рисунке 2a. Нашу расчетную схему можно разделить на три участка. I–AB, II–BC и III–CD.

2. Определим степень статической неопределенности задачи.

ССН=ЧН-ЧУ

где ЧН – число неизвестных реакций ( в нашем случае 2); ЧУ – число уравнений статики, которые можно записать для данной системы(в нашем случае 1)

ССН=2-1=1, т.е. система один раз статически неопределима.

3. Запишем уравнения равновесия бруса.

Спроецируем все силы на ось бруса

где – реакции опор.

4. Запишем полное удлинение бруса через сумму удлинений его участков.

,

где , и – удлинение участков бруса.

Рисунок 2 Образец графической части задания №1

5. Выразим удлинение каждого из участков через усилия, действующие на этом участке.

Для случая, когда продольная сила на участке постоянна, удлинение i участка определяется по следующей формуле:

,

где – продольная сила, действующая на i-ом участке; –длина i-го участка; –модуль упругости i-го участка; –площадь поперечного сечения i-го участка.

Подставляя соответствующие данные на первом участке получим:

На втором участке получим:

На третьем участке получим:

6. Получим выражение для определения продольной силы на каждом из участков (положительное направление продольной силы берем в сторону от сечения).

Применим метод сечений. (Для удобства расчетные схемы повернуты на 90^о)

Первый участок: 0 ≤ х_І ≤ с

NI =RA - Р2;

Второй участок: c ≤ х_ІІ ≤ b + c

NII =RА - P2 - Р1;

Третий участок: с+b ≤ х_ІІІ ≤ с+b+а

NIII=RА - Р2 - Р1;

7. Подставим полученные выражения для продольных сил в уравнение совместности деформаций полученное на IV этапе.

Подставив длины участков получим:

8. Решим систему из двух уравнений (уравнения равновесия и уравнения совместности деформаций) и определим реакции жестких заделок.

9. Построим эпюры продольных сил и нормальных напряжений.

Построим эпюру продольных сил, для этого подставим найденные значения реакций опор в выражения для нахождения продольных сил, полученные на VI этапе.

Первый участок:

N_I=R_A - P2 = 30,495 – 24 = 6,495кН;

Второй участок:

N_II=R_A - P2 - P1 = 30,495 – 24 – 16 = -9,505кН;

Третий участок:

N_III=R_A - P2 - P1 = 30,495 – 24 – 16 = -9,505кН

Эпюра N представлена на рисунке 2b).

Построение эпюры нормальных напряжений.

Для построения эпюры напряжений σ воспользуемся формулой

.

Тогда на первом участке имеем

На втором участке соответственно

На третьем участке:

Эпюра нормальных напряжений представлена на рисунке 2c.

10. Определим удлинения участков и построим эпюру перемещений.

Так как на каждом участке продольная сила постоянна, для определения удлинения каждого из участков воспользуемся зависимостью:

Подставляя соответствующие данные на первом участке получим:

На втором участке получим:

На третьем участке получим:

Определим перемещения границ участков:

Эпюра перемещений изображена на рисунке 2 d.