Цель работы

Целью работы является экспериментальное исследование цепи синусоидального тока, содержащей участки с индуктивно связанными элементами.

1. Общие сведения

Н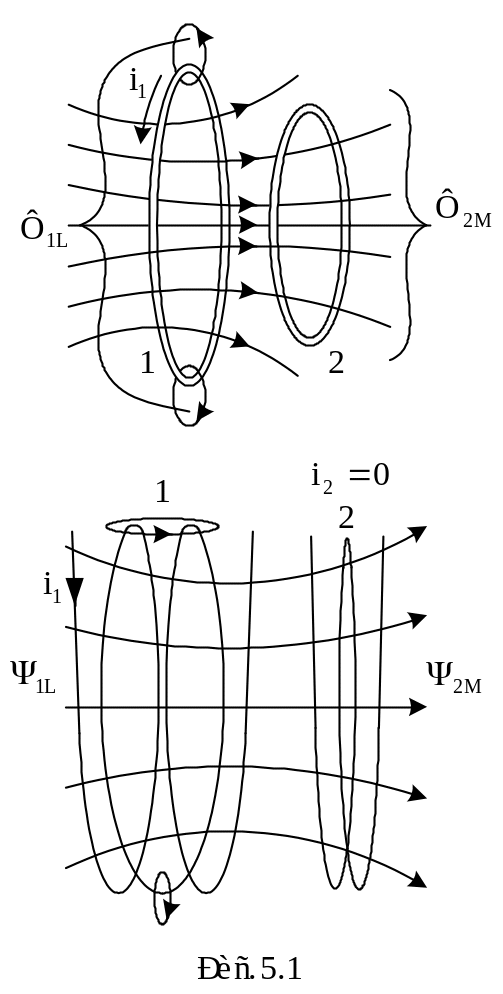 а рис. 5.1 показан контур 1 с электрическим током i₁. Магнитный поток, создаваемый этим током и сцепленный с этим контуром, называется потоком самоиндукции Φ_1L.

Расчетная величина потокосцепление самоиндукции контура 1 или неразветвленной электрической цепи обозначается Ψ_1L. В линейной электрической цепи потокосцепление Ψ_1L = L₁i₁, где L₁ собственная индуктивность или просто индуктивность контура 1.

При протекании переменного тока в окружающем контур или электрическую цепь пространстве создается переменный магнитный поток. В контуре индуцируется ЭДС самоиндукции, а на зажимах цепи возникает напряжение самоиндукции

.

Если часть магнитного потока индуктивности L₁ сцепляется с витками контура 2, в нем возникает поток взаимной индукции Φ_2М. В линейной электрической цепи потокосцепление взаимной индукции определяется выражением Ψ_2М = М₂₁i_1, где М₂₁ взаимная индуктивность контуров 1 и 2.

При изменении магнитного потока взаимной индукции во втором контуре возникает ЭДС взаимоиндукции. Напряжение взаимоиндукции

.

Напряжение на индуктивно связанных элементах электрической цепи определяются составляющими напряжений само- и взаимоиндукции. В зависимости от положительных направлений токов в магнитносвязанных катушках магнитные потоки самоиндукции и взаимоиндукции могут как совпадать по направлению (суммироваться), так и быть встречными (вычитаться). Если собственная индуктивность второго контура L_2, а напряжения на их зажимах u₁ и u₂, то в установившемся режиме в комплексной форме записи получаем:

;

.

Чтобы определить знак потока взаимоиндукции для двух магнитносвязанных катушек, вводят понятие одноименных зажимов. Выводы каждой катушки можно обозначить как начало и конец обмотки. Два зажима, принадлежащие разным катушкам с магнитной связью, называются одноименными, если при одинаковом направлении токов относительно этих зажимов магнитные потоки самоиндукции и взаимоиндукции суммируются. На схемах одноименные зажимы обозначают точками или звездочками.

Включение, при котором токи подтекают к одноименным зажимам, называется согласным.

Для последовательного согласного включения индуктивно связанных катушек (рис. 5.2) при можно записать

К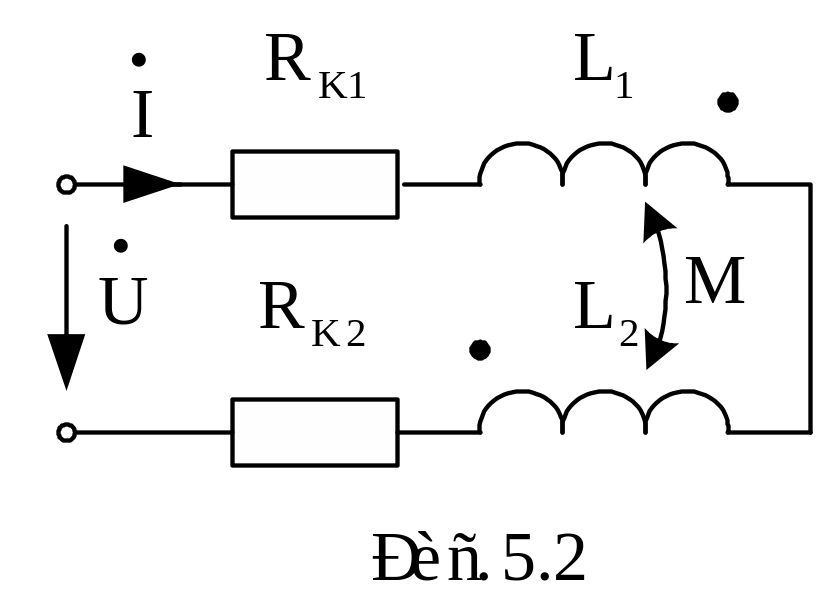 атушки соединены последовательно, поэтому протекающий по ним ток один и тот же.

Комплексное эквивалентное сопротивление цепи

.

Эквивалентное активное и реактивное сопротивления цепи:

R_эк = R_K1 + R_K2;

X_согл = ω(L₁ + L₂ + 2M).

Включение, при котором ток втекает в начало одной катушки и в конец другой, называется встречным.

Уравнения для последовательного встречного включения индуктивно связанных катушек (рис. 5.3):

Катушки соединены последовательно, поэтому протекающий по ним ток один и тот же.

Рассмотрим векторную диаграмму для этого случая. Выберем направление вектора тока по оси +1 (рис. 5.4).

По направлению вектора тока построим вектор падения напряжения на активном сопротивлении первой катушки . Под углом 90 к току в сторону опережения построим вектор напряжения на реактивном сопротивлении первой катушки . Из конца вектора  под углом 90⁰ к вектору тока в сторону отставания построим вектор напряжения . Сумма трех векторов даст вектор напряжения . Для второй катушки построение выполняется аналогично. Все векторы строятся по принципу «один из конца другого». Сумма векторов и дает вектор входного напряжения цепи.

Комплексное эквивалентное сопротивление цепи

Z_встр = ,

эквивалентное активное и реактивное сопротивления цепи:

R_эк = R_K1 + R_K2;

X_встр = ω(L₁ + L₂ - 2M).

Поскольку X_согл = ω(L₁ + L₂ + 2M) больше X_встр = ω(L₁ + L₂ - 2M), то полное сопротивление больше . Это позволяет экспериментально определить одноименные зажимы и взаимную индуктивность индуктивно связанных катушек:

.

Рассмотрим случай (рис. 5.5), когда по магнитосвязанным катушкам протекают различные токи i₁ и i₂, одинаково ориентированные относительно одноименных зажимов.

Запишем выражения мгновенных значений напряжений на катушках:

Величина M - это напряжение взаимоиндукции, которое наводится в первой катушке изменяющимся во времени током второй катушки. Это напряжение входит в уравнение со знаком « + », если токи в катушках одинаково направлены относительно одноименных зажимов.

Напряжение взаимной индукции, наведенное во второй катушке, определяется значением тока в первой катушке и равно M .

Переходя к комплексным действующим значениям токов и напряжений, можно записать:

,

где - напряжение взаимной индукции в первой катушке,

- напряжение взаимной индукции во второй катушке.

Величину  M = X_M называют сопротивлением магнитной связи.

П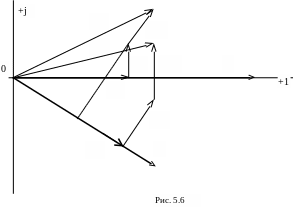 о уравнениям построим векторную диаграмму (рис. 5.6).

На комплексной плоскости изобразим векторные действующие значения токов в катушках и . (В данном случае при построении диаграммы направления и приняты произвольно). Для построения вектора напряжения на первой катушке по направлению вектора тока отложим вектор падения напряжения на активном сопротивлении катушки r₁ . Так как напряжение на индуктивности опережает ток на угол /2, под углом 90 к вектору тока из конца вектора построим вектор падения напряжения на реактивном сопротивлении катушки . Из конца вектора под углом 90 к вектору тока построим вектор напряжения взаимной индукции на первой катушке  . Сумма векторов , и согласно уравнению равна вектору .

Построение вектора напряжения на второй катушке выполняется аналогично по уравнению.

Если токи i₁ и i₂ в индуктивно связанных катушках направлены относительно одноименных зажимов по разному (рис. 5.7), то напряжение взаимоиндукции, наводимое в катушке 1 током i₂ , в уравнение для мгновенных значений напряжений и токов входит со знаком "минус":

;

Переходя к комплексным напряжениям и токам, получим:

Построение векторной диаграммы для данной цепи выполняется так же, как было описано выше, только векторы напряжений и строятся перпендикулярно векторам токов и в сторону отставания (по часовой стрелке) от соответствующего тока.

Кроме взаимной индуктивности для оценки степени магнитной связи катушек часто используется коэффициент магнитной связи

.

Явление индуктивной связи используется в трансформаторах (рис. 5.8).

Работу трансформатора без ферромагнитного сердечника можно описать следующими уравнениями по второму закону Кирхгофа:

а) для мгновенных значений

б) в комплексной форме

где - напряжение на нагрузке трансформатора.

Взаимная индуктивность М, входящая в эти уравнения, определяется из режима холостого хода трансформатора ( ). Для холостого хода действующее значение выходного напряжения U_2хх = I₁М, откуда М = или .

Векторная диаграмма трансформатора показана на рис. 5.9.

Построение начато с вектора тока .

Этот вектор отложен по оси +1. Далее выполняют построения в соответствии с уравнением. Пусть сопротивление нагрузки имеет активно-индуктивный характер  , тогда вектор напряжения опережает вектор тока на угол _н. Из конца вектора параллельно вектору тока построен вектор падения напряжения на сопротивлении вторичной обмотки .

Вектор падения напряжения на индуктивном сопротивлении вторичной обмотки построен из конца вектора под углом 90⁰ к вектору тока в сторону опережения. Из уравнения (4.8) следует, что сумма вектора напряжения взаимной индукции и трех ранее построенных векторов равна 0, поэтому вектор, соединяющий начало координат с концом вектора , равен и направлен к точке 0.

Вектор тока в первичной цепи трансформатора на 90⁰ отстает от вектора . Он построен из начала координат перпендикулярно вектору . Затем в соответствии с уравнением строятся векторы падения напряжения на элементах первичной цепи трансформатора и находится вектор входного напряжения .