30. Кривые Безье.

В общем случае, кривая Безье задается векторным уравнением

(10) , где , ,

а - вершины так называемого определяющего многоугольника.

Кривые Безье названы в честь предложившего их французского ученого П. Безье (Bezier).

Кривые Безье обладают следующими свойствами:

1. Степень кривой N на единицу меньше числа вершин определяющего многогранника. Для двух точек кривая Безье превращается в отрезок прямой.

2. Начинается в точке 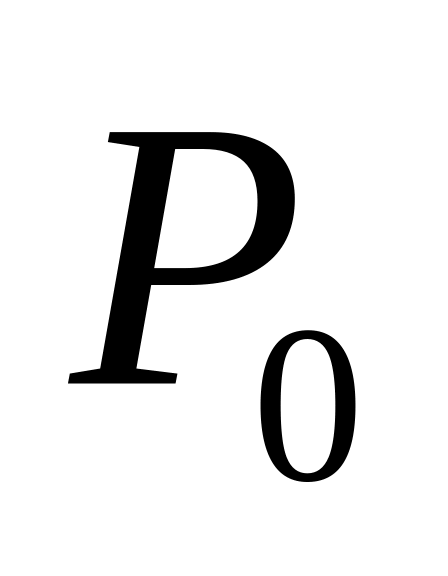и заканчивается в точке .

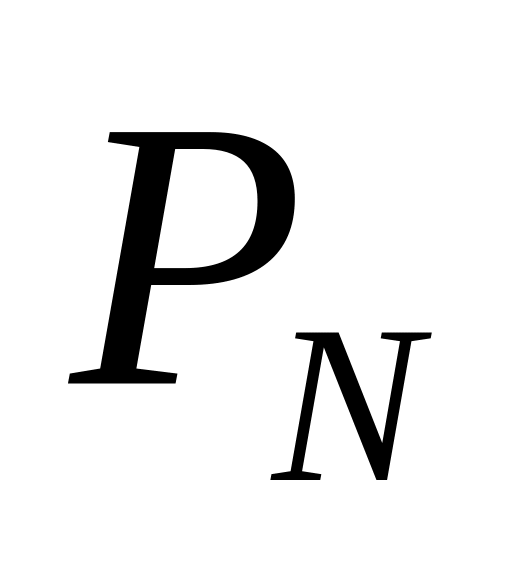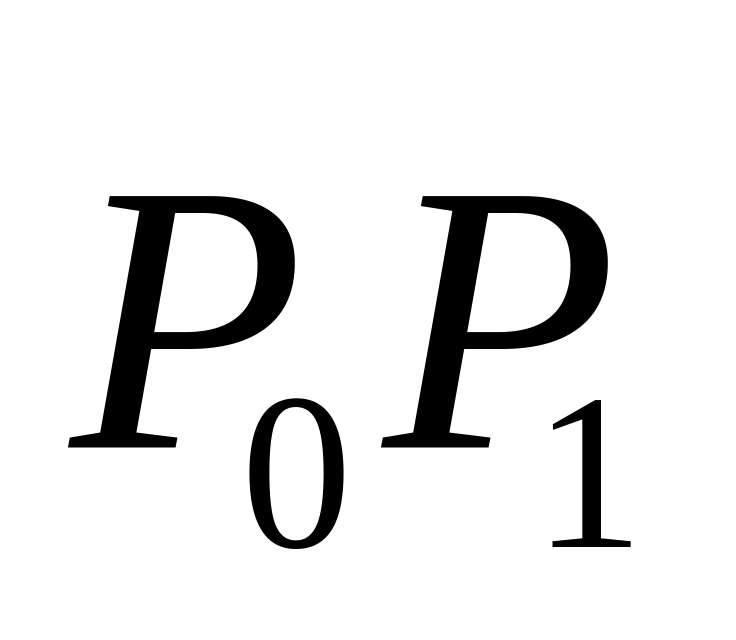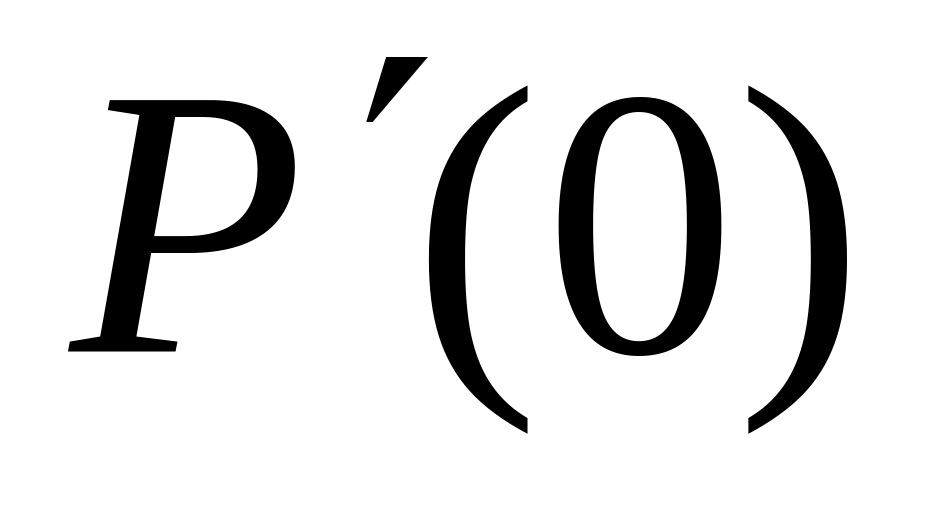3. Вектор сонаправлен с вектором касательной к кривой в ее начальной точке . Вектор 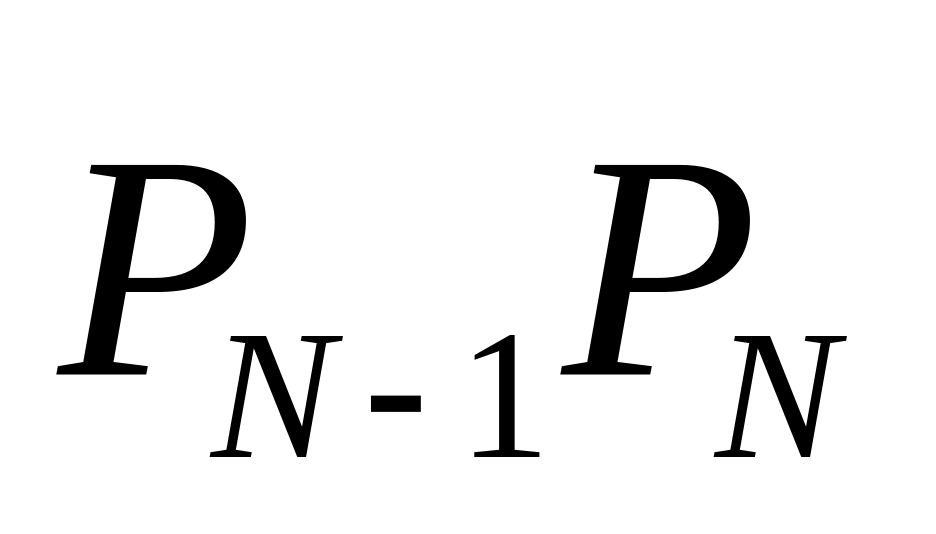сонаправлен с вектором касательной к кривой в ее конечной точке .

4. Целиком лежит внутри выпуклой оболочки определяющего многоугольника.

Для нас наибольший интерес представляет частный случай кривой Безье – кривая Безье третьей степени (кубическая), создаваемая по четырем точкам. При N=3 выражение (10) примет вид:

(11) , ,

Кубические кривые Безье можно использовать в задачах сплайновой интерполяции для представления сегментов, если считать точки и узлами интерполяционного сплайна, а точки и - управляющими точками сегмента.

Для построения цепочки кубических сегментов Безье используется метод

Graphics.DrawBeziers(Pen, Point[]). Для задания N сегментов требуется 4 + 3N точек, т.к. последняя точка любого внутреннего сегмента является первой следующего. Непрерывность касательной вдоль всего сплайна в этом методе не обеспечивается. Чтобы обеспечить непрерывность касательной, следует подбирать управляющие точки таким образом, чтобы каждый внутренний узел сплайна был серединой отрезка, соединяющего контрольную точку предыдущего сегмента и контрольную точку следующего сегмента.

31. Поверхности Безье.

Как и кривые, поверхности в компьютерной графике обычно задаются параметрически. (1) 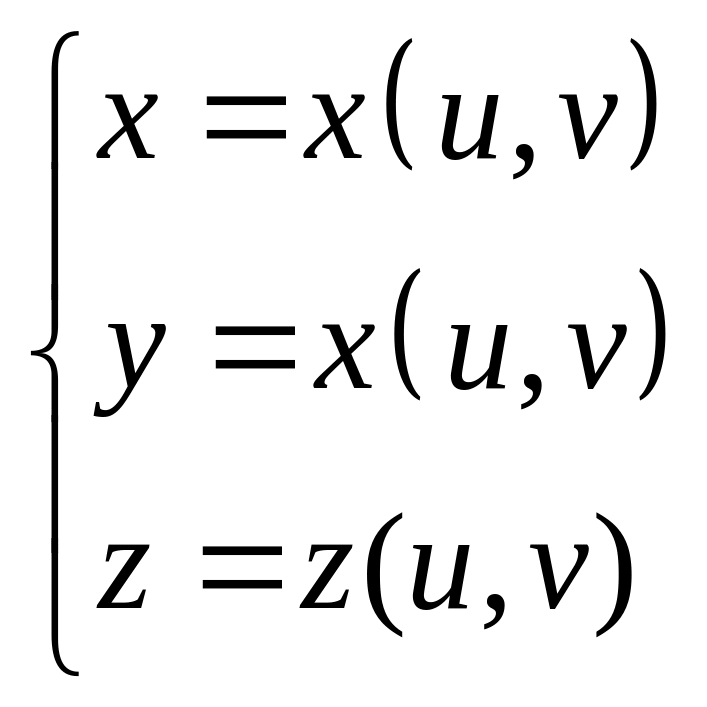, где и - независимые параметры.

В матричной форме уравнение (1) записывается как

(2) , где 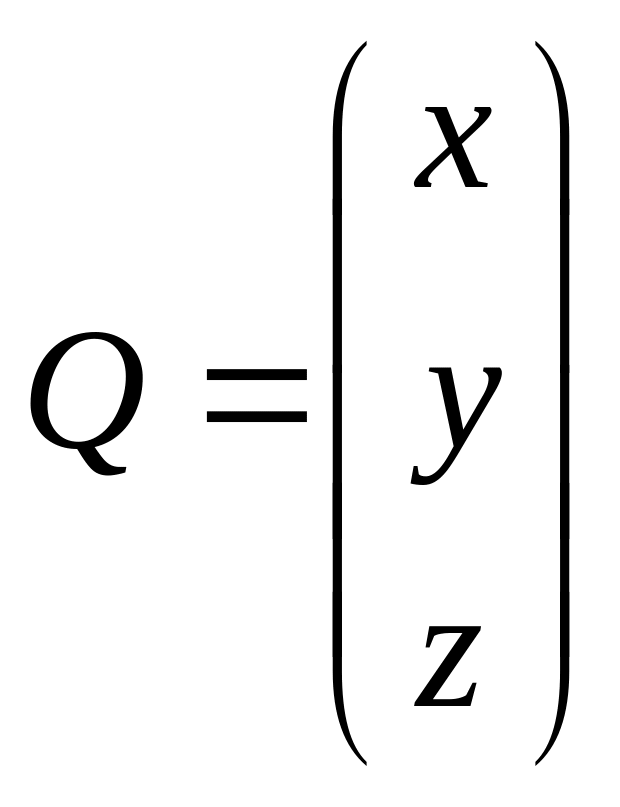– множество точек в пространстве, образующих поверхность.

Как и в случае кривых, диапазон изменения параметров зависит от выбранного способа параметризации. При нормальной параметризации, т.е. при которой значения и нормированы, точка с координатами ( ; ) принадлежит единичному квадрату.

Е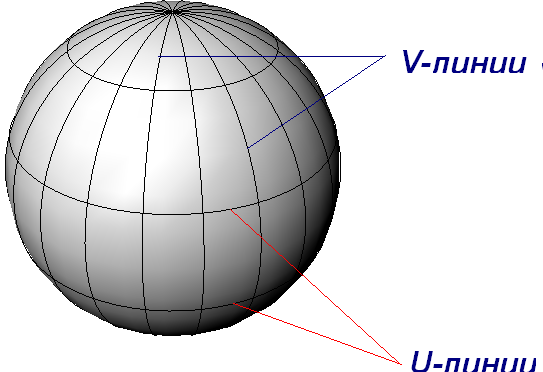 сли зафиксировать некоторое значение параметра и изменять значение параметра , то получится линия в пространстве, описываемая уравнением и называемая v-линией. Таким образом, набор фиксированных значений u порождает семейство v-линий. Аналогично определяются u-линии. Построив некоторое количество u-линий и v-линий, получим сетку топологически ортогональных параметрических кривых, каждая из которых принадлежит исходной поверхности. Параметры u и v являются внутренними криволинейными координатами на поверхности Q.

Поверхность Безье степени NxM задается выражением

(8) , где , ,

Д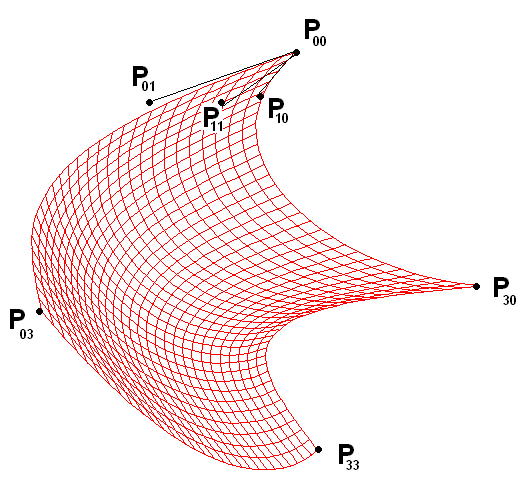 ля определения такой поверхность Безье требуется задать (N+1)x(M+1) точек. Чаще всего используются бикубические поверхности Безье (N=3, M=3), задаваемые 16-ю точками. Границами такого бикубического сегмента поверхности Безье являются кубические кривые Безье.

Подобно тому, как промежуточные управляющие точки кубической кривой задают направления касательных на ее концах, векторы и коллинеарны касательным к границам поверхности в точке . Вектор коллинеарен вектору кручения .